FORM FOUR MATHEMATICS EXAM SERIES 221
FORM FOUR MATHEMATICS EXAM SERIES 221
PRESIDENT OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS
FORM FOUR
TERMINAL EXAMINATION - MAY, 2023
TIME 3:00 HOURS
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in section A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your examination number on every page of your answer booklet(s)
SECTION A (60 Marks)
Answer all questions in this section.
1. ![]()
![]()
![]()
![]()
![]()
2. ![]()
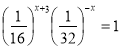
![]()
3. (a) A box contains 4 white balls and 5 black balls. Two balls are selected at random without replacement. Find the probability that
(i) Both are white balls
(ii) The first is black and the second is the white ball
(b) In a class of 15 students who take either Mathematics or Biology, 12 students take Mathematics, 8 students take Biology. If each student takes either subjects find by using formula the number of students who take Biology but not Mathematics.
4. (a) The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
(b) The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
5. (a) The area of the triangle ABC is 140 cm2, AB = 20, AC = 14cm, find the angle BAC
(b) Triangle XYZ is similar to triangle ABC and XY = 8 cm. If the area of the triangle XYZ is 24 cm2 and the area of the triangle ABC is 96 cm2. Calculate the length of AB.
6.![]()
![]()
![]()
![]()
![]()
7. ![]()
![]()
![]()
![]() =
=
![]() /=
/=
19 bought Shelves for cash 110,000/=
20 sold goods for cash 900,000/=
21 purchases goods for cash 800,000/=
22 sold goods for cash 1, 400,000/=
26 paid rent 300,000/=
Record the above transactions in Cash account ledger and extract a Trial balance.
8. (a). The product of a three terms of a geometric progression (GP) is 8000. If the first term is 4. Find the second term and third term
(b). Mahona invested a certain amount of money in a Savings Bank whose interest rate was 10% compounded annually. After two years he got 5000 shillings.
- How much did he invest at the start?
- How much did he receives as Interest at the end of two years.
9. (a) Find the value of
Sin (1500) cos (3150) Without using mathematical tables
Tan (3000)
(b) Calculate the angles of a triangle which has sides of lengths 4m, 5m and 7m
10. (a). Given that x2 –y2 = 27 and x + y = 9 find the value of xy
(b). Solve the equation 2x2 – 3x – 5 = 0 by completing the square.
SECTION B (40 Marks)
Answer all questions
11. (a) The number of workers absent in 52 working days is given in a cumulative frequency table below
| No.of absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 - 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find (i) Percentage of workers who are absent at least for 20 days
(ii) Median
(b) Find the angle x in the figure below
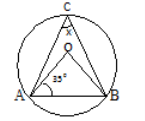
12. (a) A ship sails from point A (40![]() ) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and
) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and ![]() (give your answer in nearest degree)
(give your answer in nearest degree)
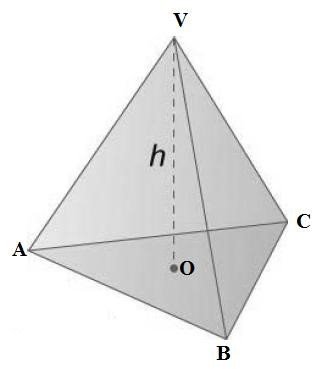
(b) VABCD is a pyramid with VA=VB=VC=VD=5cm and ABCD is a square base of sides 4cm each. Assume that the centre of the base is at point N. Find
- The angle between VA and the base ABCD
- The volume of the pyramid
13. ![]()
![]()
![]()
![]()
![]()
14. (a). A function F is defined by the formula f(x) = ![]() where x is a whole number
where x is a whole number
- If f(x) = 25 find the value of x
- Find the value of
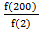
(b). A craftsman wishes to decide how many of each type A and B charcoal stove he has to fabricate in order to maximize profit for this month. Unit profit for type A stove is shs. 1000 and Unit profit for type B is shs. 1500. Type A stove requires 1m2 of mild steel sheet per unit and type B requires 2m2. He has only 12 m2 of mild steel available. He can fabricate a total of 8 stoves of either type per month. How many of each type should he fabricate?
FORM FOUR MATHEMATICS EXAM SERIES 157
FORM FOUR MATHEMATICS EXAM SERIES 157
OFFICE OF THE PRESIDENT, MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
TERMINAL EXAMINATIONS- MAY 2022
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a) By using mathematical table evaluate ![]() to three significant figures taking
to three significant figures taking ![]()
(b)If ![]() Find Z = x + y hence express Z as fraction in its lowest form.
Find Z = x + y hence express Z as fraction in its lowest form.
2(a) Simplify ![]()
(b)Solve the equation ![]()
3.(a)Given ![]() then find
then find ![]()
(b)In class of 25 students, 12 students have taken mathematics, 8 have taken Biology. Represent this information on the Venn diagram hence or otherwise find number of students who.
- Have taken mathematics and biology
- Biology but not mathematics
4(a)If Alice deserves twice as many marks as Brenda and Brenda deserve half as much as many marks as Catherine, how many marks does each deserve when their total marks are 125.
(b)Given the vector ![]() determine;
determine;
- The value of k such that
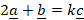
- A unit vector parallel to
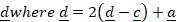
5(a)The radius of the circle which inscribe an equilateral triangle is 2cm, find the perimeter of the triangle correct to two decimal places.
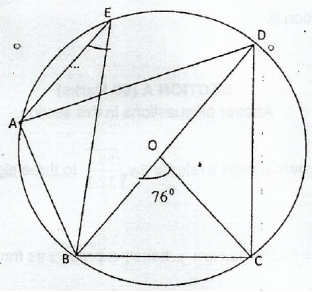
(b)In the diagram below O is the centre and ![]() is the diameter of the circle
is the diameter of the circle ![]() If
If ![]() and
and ![]() Find the size of the angles of Quadrilateral ABCD
Find the size of the angles of Quadrilateral ABCD
6(a)The mass of a plastic disc is inversely proportional to its area. If a disc of area 180cm2 has a mass of 200g
- Write down the equation relating mass (M) and area(A) of a disc.
- If a similar disc has mass of 250g what is its area?
(b)Given ![]() make t the subject of the formula
make t the subject of the formula
7.(a) If ![]() determine
determine ![]()
(b)The sides of the rectangle are in the ratio 4:5. Given that the area of this rectangle is 20cm2. Find the dimension of the rectangle.
8(a)The seventh term of a geometric progression is eighth times the fourth term and the fifth term is 48, find the term and the common ratio.
(b)A display of beef masala in supermarket is to have the form of a pyramid with 20 cans in the bottom row, 19 on the next row, 18 cans on the next row, and so on, with a single can at the top. How many cans of beef masala will be required for the display?
9.(a)If A and B are two complementary angles and ![]() find
find ![]() hence use the results to verify that
hence use the results to verify that ![]()
(b)A man 12m directly away from a tree and from this position the angle of elevation of the top of the tree is 24°. If the measurement is taken from a point 1.5m above the ground level, find the height of the tree.
10(a)By completing the square solve the quadratic equation ![]()
(b)Given ![]() Find
Find
- The value of a and b
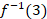
SECTION B (40 MARKS)
Answer Any Four Questions from this section
11.One end of the rectangular tank of length 6m is a square ![]() of side 2m. If AP is a diagonal of the tank, calculate;
of side 2m. If AP is a diagonal of the tank, calculate;
- AP correct one decimal places
- The angle between AP and the plane ABCD
- The surface area of the tank.
12.From a linear programming problem the following graph is draw
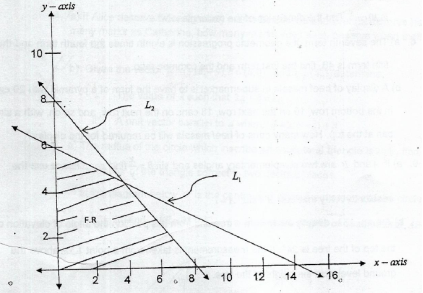
From the graph
- Find the equation of lines L1 and L2
- Write down the four inequalities representing the shaded region
- Determine the corner points of the feasible region
- Maximize the objective function
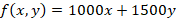 subjected to constraints in (ii)above
subjected to constraints in (ii)above
13.The number of workers in 52 working days is given in a cumulative frequency table below.
| Number of absences | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find;
- The percentage of workers who are absent at least 20days
- Mean, use assumed mean A=17
- Median
14.The following information relates to Mr. Mtipanga a trade as 31st December, 2011
Net profit 2,000,000/=
Cost of sales 60% of sales
Purchases 8,000,000/=
Closing stock 20% of purchase
Sales to Net profit ratio 10:1
Determine
- Sales
- Cost of sales
- Closing stock
- Opening stock
- Expenses
15.(a)Find the image of the point (1, -5) after reflection on the line x=0, and then translated by a vector a= (0, -6)
(b)![]() find two values of k such that
find two values of k such that ![]()
(c) Find the inverse of matrix ![]() hence use the results to solve the system of equations
hence use the results to solve the system of equations![]()
16(a)A bag contains 24 tennis balls, some white and some green. If a ball is chosen at random the probability of getting a green ball is ![]() . How many white balls are there?
. How many white balls are there?
(b)The probability that it’s raining at 8:30am on any one day is ![]() The probability that a boy wears a rain coat as he leaves for school at 8:30am is
The probability that a boy wears a rain coat as he leaves for school at 8:30am is ![]() if it rain at any time. If it is not raining the probability that he wear a coat is
if it rain at any time. If it is not raining the probability that he wear a coat is ![]() . What is the probability that he wear a coat on any one day?
. What is the probability that he wear a coat on any one day?
FORM FOUR MATHEMATICS EXAM SERIES 93
FORM FOUR MATHEMATICS EXAM SERIES 93
OFFICE OF THE PRESIDENT, MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
TERMINAL EXAMINATIONS- MAY 2022
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a) By using mathematical table evaluate ![]() to three significant figures taking
to three significant figures taking ![]()
(b)If ![]() Find Z = x + y hence express Z as fraction in its lowest form.
Find Z = x + y hence express Z as fraction in its lowest form.
2(a) Simplify ![]()
(b)Solve the equation ![]()
3.(a)Given ![]() then find
then find ![]()
(b)In class of 25 students, 12 students have taken mathematics, 8 have taken Biology. Represent this information on the Venn diagram hence or otherwise find number of students who.
- Have taken mathematics and biology
- Biology but not mathematics
4(a)If Alice deserves twice as many marks as Brenda and Brenda deserve half as much as many marks as Catherine, how many marks does each deserve when their total marks are 125.
(b)Given the vector ![]() determine;
determine;
- The value of k such that
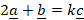
- A unit vector parallel to
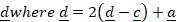
5(a)The radius of the circle which inscribe an equilateral triangle is 2cm, find the perimeter of the triangle correct to two decimal places.
(b)In the diagram below O is the centre and ![]() is the diameter of the circle
is the diameter of the circle ![]() If
If ![]() and
and ![]() Find the size of the angles of Quadrilateral ABCD
Find the size of the angles of Quadrilateral ABCD

6(a)The mass of a plastic disc is inversely proportional to its area. If a disc of area 180cm2 has a mass of 200g
- Write down the equation relating mass (M) and area(A) of a disc.
- If a similar disc has mass of 250g what is its area?
(b)Given ![]() make t the subject of the formula
make t the subject of the formula
7.(a) If ![]() determine
determine ![]()
(b)The sides of the rectangle are in the ratio 4:5. Given that the area of this rectangle is 20cm2. Find the dimension of the rectangle.
8(a)The seventh term of a geometric progression is eighth times the fourth term and the fifth term is 48, find the term and the common ratio.
(b)A display of beef masala in supermarket is to have the form of a pyramid with 20 cans in the bottom row, 19 on the next row, 18 cans on the next row, and so on, with a single can at the top. How many cans of beef masala will be required for the display?
9.(a)If A and B are two complementary angles and ![]() find
find ![]() hence use the results to verify that
hence use the results to verify that ![]()
(b)A man 12m directly away from a tree and from this position the angle of elevation of the top of the tree is 24°. If the measurement is taken from a point 1.5m above the ground level, find the height of the tree.
10(a)By completing the square solve the quadratic equation ![]()
(b)Given ![]() Find
Find
- The value of a and b
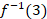
SECTION B (40 MARKS)
Answer Any Four Questions from this section
11.One end of the rectangular tank of length 6m is a square ![]() of side 2m. If AP is a diagonal of the tank, calculate;
of side 2m. If AP is a diagonal of the tank, calculate;
- AP correct one decimal places
- The angle between AP and the plane ABCD
- The surface area of the tank.
12.From a linear programming problem the following graph is draw

From the graph
- Find the equation of lines L1 and L2
- Write down the four inequalities representing the shaded region
- Determine the corner points of the feasible region
- Maximize the objective function
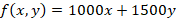 subjected to constraints in (ii)above
subjected to constraints in (ii)above
13.The number of workers in 52 working days is given in a cumulative frequency table below.
| Number of absences | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find;
- The percentage of workers who are absent at least 20days
- Mean, use assumed mean A=17
- Median
14.The following information relates to Mr. Mtipanga a trade as 31st December, 2011
Net profit 2,000,000/=
Cost of sales 60% of sales
Purchases 8,000,000/=
Closing stock 20% of purchase
Sales to Net profit ratio 10:1
Determine
- Sales
- Cost of sales
- Closing stock
- Opening stock
- Expenses
15.(a)Find the image of the point (1, -5) after reflection on the line x=0, and then translated by a vector a= (0, -6)
(b)![]() find two values of k such that
find two values of k such that ![]()
(c) Find the inverse of matrix ![]() hence use the results to solve the system of equations
hence use the results to solve the system of equations![]()
16(a)A bag contains 24 tennis balls, some white and some green. If a ball is chosen at random the probability of getting a green ball is ![]() . How many white balls are there?
. How many white balls are there?
(b)The probability that it’s raining at 8:30am on any one day is ![]() The probability that a boy wears a rain coat as he leaves for school at 8:30am is
The probability that a boy wears a rain coat as he leaves for school at 8:30am is ![]() if it rain at any time. If it is not raining the probability that he wear a coat is
if it rain at any time. If it is not raining the probability that he wear a coat is ![]() . What is the probability that he wear a coat on any one day?
. What is the probability that he wear a coat on any one day?
FORM FOUR MATHEMATICS EXAM SERIES 92
FORM FOUR MATHEMATICS EXAM SERIES 92
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
FORM FOUR BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 3 Hours Year: 2021
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions.
2.Answer all questions in sections A and B.
3.Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
5.NECTA mathematical tables and non-programmable calculator may be used.
6.All communication devices and any unauthorized materials are not allowed in the examination room.
7.The following constants for your calculations
Radius of the Earth =6370km, ![]()
SECTION A (60 Marks)
Answer All Question In This Section
1.(a) Calculate without using Mathematical tables, correct to two decimal places
![]()
(b) Each student of Leo academy belongs to one club. ![]() are members in drama club.
are members in drama club. ![]() are members in mathematics club and the number of science club is twice that of drama club .The rest are members of research club. What fraction of students are members of research club? 2. (a) Make x subject of the formula
are members in mathematics club and the number of science club is twice that of drama club .The rest are members of research club. What fraction of students are members of research club? 2. (a) Make x subject of the formula
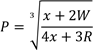
(b)Three variables p, q and r are such that p varies directly as q and inversely as square of r. When p=9, q=12 and r=2. Find p when q=15 and r=5.
3.(a) ) Given that ![]() and
and ![]() , where X is an integer. Represent this in a venn diagram, hence find elements of:
, where X is an integer. Represent this in a venn diagram, hence find elements of:
(i)AuB
(ii)AnB
(b) In a school of 95 pupils, 42 of the pupils take Biology but not Chemistry, 32 take both subject and 10 of them take Chemistry but not Biology. How many pupils do not take either Biology or Chemistry?
4.(a) Let P and Q be two points at (2,5) and (4, -1) respectively. Find
(i)Find equation of the line that passes through the midpoint of PQ and is perpendicular to it in form of ax + by +c=0
(ii)The distance between P and Q
(b) A chord is 6cm from the center of a circle with radius 10cm. What is the length of a chord?
5.(a) In triangle PQR, PR=5cm, PQ=6cm and
(i)The length of side QR
(ii) (b) The size of the exterior angle of a regular polygon is 450. Find (i)The number of sides (ii)The sum of all interior angles. 6.(a) Given t=3x , by using the substitution solve the equation 32(1+x) - 3x =3(x+3) - 3 (b) A shopkeeper makes a profit of 40% by selling an article for T.Sh. 63,000/=. What would be his percentage loss if he sold the article for T,Sh. 40,000/= 7.(a) Prepare the balance sheet for the balances given below Capital 4,500,000/= Drawings 800,000/= Creditors 430,000/= Closing stock 500,000/= Debtors 800,000/= Buildings 1,600,000/= Motor Van 800,000/= Bank 400,000/= Cash 900,000/= Net profit 270,000/= Loan 600,000/= (b) What is the aim of preparing balance sheet 8.(a) The third, fifth and eighth terms of arithmetic progression A.P form the first three terms of Geometric Progression G.P . If the common difference of the A.P is 3, find (i)The first term of the G.P (ii)The sum of the first 9 terms of the G.P to one decimal place. (b) Find the sum of first eight terms of the following sequence 1, -2, 4, -8 . . . . . 9. (a) In the figure below BD=5cm, DC=5cm and DE=3cm. Find length of AC and AE (b) A plane is flying at a constant height. The pilot observed of an angle of depression of 270 to one end of the lake and 150 to the opposite end of the lake. If the lake is 12 km long. Determine the altitude of the plane. 10. (a) 10 years ago a man was 12 times as old as his son and 10 years from now a man will be twice as old as his son. Find their present age. (b) Find the values of x that satisfy the equation log(x+5) + log(x + 2) = log4 SECTION B ( 40 marks) Answer all questions from this section. 11. The examination scores in Basic Mathematics of 40 Form IV students are given in the following cumulative frequency table Class Interval 10-19 20-29 30-39 40-49 50-59 60-69 Cumulative Frequency 3 6 12 22 35 40 (a)Find the mean score using assumed mean A=44.5 (b)Draw Histogram and use it to estimate the mode (c)Calculate the median 12.(a) The two towns P and Q lie on the earths surface such that P(650N, 960E) and Q(650N, 840W). Find the distance between the towns in kilometers and nautical miles. (b) The figure below shows a tetrahedron. The length of each edge is 8cm. O is the centre of triangle ABC. Calculate (i)The length of VO (ii)The angle between line AV and the plane ABC (c) Find the volume of a cone which has a base diameter of 10 cm and slant height of 13 cm. 13. (a) The matrices are such that AB=A + B. Find the values of a, b, c and d (b)Triangle PQR vertices at P(2, 2), Q(5, 3) and R(4, 1) is mapped onto triangle PQR by transformation matrix Find coordinate of triangle PQR (c)Determine the values of x which the matrix below has no inverse 14.(a)Given that h(x)= -1 - | x + 3| i.Sketch the graph of h(x) ii.Use the graph to deduce domain and range (b) The manager of a car park allows 10m2 of parking space for each car and 30m2 for each lorry. The total space available is 300m2. He decides that the maximum number of vehicles at any time must not exceed 20 and also insists that there must be at least as many cars as lorries. If the number of cars is X and the number of lorries is Y. (i) Write down the inequities which must be satisfied (ii)If the parking charge is sh.10 for each car and sh.50 for each lorry. How many vehicles of each kind he should admit to maximize his income and calculate his income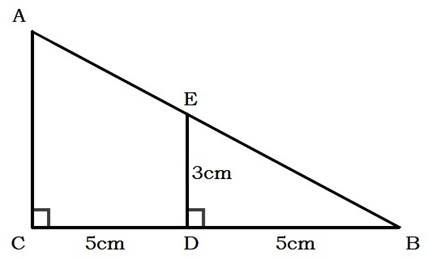
![]() and
and ![]()
![]()
![]()
![]()
FORM FOUR MATHEMATICS EXAM SERIES 53
FORM FOUR MATHEMATICS EXAM SERIES 53
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256