.
.FORM THREE MATHEMATICS EXAM SERIES 228
FORM THREE MATHEMATICS EXAM SERIES 228
PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM THREE
TERMINAL EXAMS MAY – 2023
041
TIME: 3HOURS
INSTRUCTION
- This paper consists of two sections A and B with total of fourteen (14) questions
- Answer all questions
- Programmable calculators, phones and any other unauthorized materials are not allowed in examination room
- Write your examination on every page of your answer sheet provided
- All diagrams must be drawn in pencils
- All writings must be in black/blue ink
SECTION A. 60 MARKS
1. (a) Equal squares as large as possible are drawn on a rectangular board measuring 54cm by 78cm. Find the largest size of the squares.
(b) (i) Express 2.7?9? as a fraction in the form a/b where a and b are integers and b≠0
(ii)Arrange 2/5, 5/8 ,48% and 0.6 in ascending order
(iii) Show on the number line the solution set of the inequality
?2x+1?>3
2. (a) i. If x2 +ax +4=0 is a perfect square . Find the value of a
ii. If x2 +bx +c =(x-3)(x+2) determine the values of b and c
iii. Solve the following quadratic equation by complete the square method x2 + 6x +7=0
(b) i. Solve 3 - of (6x+9) = 5-2x
ii. If U*V =UV+V, Find x given that (x*2)*5=60
3. (a) Rectangular table top is 2m long. If the area of the rectangular table top is
3.96m2. find its width
(b) i. Solve the following simultaneous equations
2x+3y=5
4x+23=5y
ii. If Fatuma is 4 years less than Bakari and 3 times Fatuma's age is equal to 2 times Bakari's age. What are their ages ?
4. (a) If find the value of t
(b)Write “L” in terms of M, N and T from the formula
(c) Determine the value of x if
5. (a)If the 5th term of an arithmetic progression is 23 and the 12th term is 37, find the first tem and the common difference.
(b) In how many years would one double one’s investment if Tshs 2500 is invested at 8% compounded semi –annually.
6. (a) If y varies inversely as and x is multiplied by n. What is the ratio of the first y to the second y?
(b) The headmaster has enough food to last for his 600 students for 20 days from tomorrow. If 120 students leave the school today for UMISSETA game, how long will the food last?
7. (a) The sum of the first six terms of an A.P is 72 and the second term is seven times the fifth term.
- Find the first term and the common difference
- Find the sum of the first ten terms
(b) Find the sum of the first four terms of a geometric progression which has a first term of 1 and a common ratio of
8. (a) The gradient of line L1is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
(b) The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
9. (a) Find the value of
Without using mathematical tables.
(b) Calculate the angles of a triangle which has sides of lengths 4m, 5m and 7m
10. (a). Given that x2 –y2 = 27 and x + y = 9 find the value of xy
(b). Solve the equation 2x2 – 3x – 5 = 0 by completing the square.
SECTION B (40 Marks)
Answer all questions
11. (a) The number of workers absent in 52 working days is given in a cumulative frequency table below
| No.of absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 - 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find
- Percentage of workers who are absent at least for 20 days
- Median
(b) Find the angle x in the figure below
12. (a) A ship sails from point A (40) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and
(give your answer in nearest degree)
(b) VABCD is a pyramid with VA=VB=VC=VD=5cm and ABCD is a square base of sides 4cm each. Assume that the centre of the base is at point N. Find
(i) The angle between VA and the base ABCD
(ii) The volume of the pyramid
13. (a) If tan A = , where A is an obtuse angle,
Find (i). Cos A + Sin A (ii). – Cos2 A – Sin2 A
(b) A and B are two points on the ground level and both lie west of flagstaff. The angle of elevation of the top of the flagstaff from A is 560 and from B is 430. If B is 28m from the foot of the flagstaff. How far apart are the points A and B?
14. (a)The marks in basic Mathematics terminal Examination obtained by 40 students in one of the secondary school in Katavi were as follows;
60, 54, 48, 43, 37 61, 43, 66, 65, 52, 37, 81, 70, 48, 63, 74, 67, 52, 48, 37, 48 42, 43, 52, 52, 22, 27, 37,44 38, 29, 19, 28 36, 42, 47, 36, 52, 50, 28.
- Prepare a frequency distribution table with class intervals 10 – 19, 20 – 29, etc.
- Find the class which contain the median
- Find the mean
- Calculate the median.
(b) A field is 10m longer than its width. The area is 7,200m2. What is the width?
FORM THREE MATHEMATICS EXAM SERIES 135
FORM THREE MATHEMATICS EXAM SERIES 135
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM THREE BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 3:00 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorized materials are not allowed in the examination room.
SECTION A
ANSWER ALL QUESTIONS
1. (a) Write ![]() as a mixed fraction
as a mixed fraction
(b)If ![]() and
and ![]() find x + y to 3-significant figure
find x + y to 3-significant figure
2. (a)Find ![]()
(b) A farmer sold a quarter of his maize harvest and gave one third of the remaining to his relatives.
If the farmer remained with 25 bags. If maize, how many bags of maize did the farmer harvest?
3. (a)Factorize (i) ![]()
(ii) ![]()
(b)Simplify ![]()
(c)Solve for x: ![]()
4. (a)Solve for x: (i) ![]()
(ii) ![]()
(b)If log3 = 0.4771 and log2 = 0.3010
Find:
(i)![]()
(ii)![]() Without using tables.
Without using tables.
5. Solve the following simultaneous equations
6. Given the universal
Set ![]() and
and ![]()
- Represent the above information in a Venn-diagram and use it to find elements of
![]()
- Show that
![]()
7. (a)Marium served Tshs 6 million in a serving account Bank where interest rate was 10% compounded annually. Find the amount in mariam’s account after 5years.
(b)In how many years would one’s investment double if 100,000/= is invested at 10% compounded semi-annually?
8. (a) Factorize:
![]()
![]()
(b) Given that
AB=EC
![]()
![]()
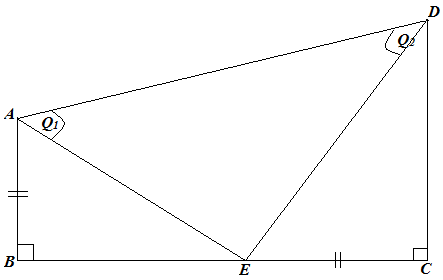
- Show that EA=ED
- Prove that
![]() and state the postulate out of (SSS, AAS, SAS, RHS)
and state the postulate out of (SSS, AAS, SAS, RHS)
9. (a)The ratio of the areas of two similar polygons is 144:225. If the length of a side of the smaller polygon is 60cm, find the length of the larger polygon
(b)
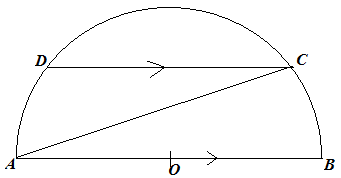
Given that
- DC//AB
- AOB is diameter
![]()
Find an expression in terms of x
![]()
10. In a series between the integers 3 and 102. Find the sum of
- Even numbers (ii) Odd numbers
(b) A bacteria produces 10 bacteria after every minute and each of the 10 bacteria produces, 10 bacteria after every minute and so
- Form a sequence of number of bacteria produced after 1,2,3 and 4 minutes
- If the frequency is to form a series, what is the name of the series?
- Find the sum of bacteria produced after one hour.
SECTION B (Answer All Questions)
11. The table below represents the scores in general cleanliness of 30 students
| SCORE x | FREQ f | fx |
| 1 | M |
|
| 2 | 2m |
|
| 3 | 10 |
|
| 4 | 8 |
|
| 5 | 3 |
|
|
| ?f | ?fx |
- Find the value of m
- Complete the table and find ?f, ?fx
- Find the mean (average) score
- Find the mode
- Construct an ogive and use it to estivate the median
12. Given the function f(x) = x2-8x + 12
- Find the x and y-intercepts
- Using (a) determine the axis of symmetry of f(x)
- Using (b) determine the coordinates of the minimum point
- Using (a) (b) and (c) sketch the graph of f(x)
- From the graph find
- Domain (ii)Range
- Construct a suitable line and sketch it on the same axes to find solution of the equation; x2 -10x + 16=0
13. (a)An aero plane fires from Tabora (5°S, 33°E) to Tanga (5°S, 39°E) at 332 km/her. Along parallel latitudes. If it leaves Tabora at 3 p.m., find the time of arrival at Tanga air-port
(b)Another plane flying at 595 km/hr leaves Dsm (7°S,39°E) at 8:00a.m it Addis Ababa (9°N, 39°E) (parallel longitude)
(Radius of the earth R![]() 6370km)
6370km)
14. (a) The volume V of a given mass of gas varies directly as the absolute temperature T and inversely as the pressure P
If V=450 and T= 288 when P=825, find V when T=320 and P = 720
(b) In the figure below, BD is a tangent to the circle having the centre O .
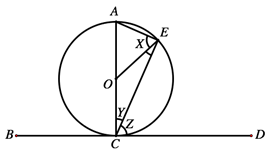
Given that angle OEC = 28°, find the values of angles marked X , Y and Z .
FORM THREE MATHEMATICS EXAM SERIES 92
FORM THREE MATHEMATICS EXAM SERIES 92
OFFICE OF THE PRESIDENT, MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
TERMINAL EXAMINATIONS- MAY 2022
FORM THREE BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a)If a*b=b (a2 – 2b) Find (i) 3*2 (ii) n if 4*n=0
(b)Given
![]()
![]()
2.A and B are two sets such that
-
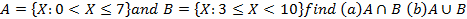
- In a class of 30 students 17 participate in English debate, 12 participate in English debate and sports. If every student is required to participate in at least one of the two subjects. Find the number of students who participate in
(i) English debate only (ii) Sports only
3.(a)If ![]()
(b)Express as single logarithm the expression ![]()
4.Rewrite without absolute value ![]() and sketch a graph of the resulting inequality
and sketch a graph of the resulting inequality
5.(a)The second term of an A.P is 2 and the sixth term is 14. Find
- The first term
- The common difference
(b)A function is defined by ![]() . Find
. Find
(i) The inverse ![]() of this function (ii)
of this function (ii)![]()
6.Given that ![]() find value of
find value of
- Cos A
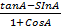
7.Fine the remainder when ![]() is divided by x + 1 and hence solve the equation
is divided by x + 1 and hence solve the equation ![]()
8.If ![]() evaluate
evaluate
- Correct to 3 decimal places
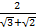
- Simplify
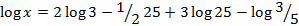
- Given
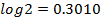 and
and 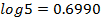 find
find 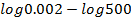
9.
- Given that
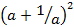 = find value of
= find value of 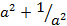
- Make q the subject of the equation
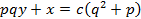
- Solve the equation
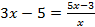 by factorization
by factorization
10. A line passes through point A (3,5) and B (8, K) has a slope of -2. Find the;
- Value of K
- The equations of line
SECTION B
11.(a)Mpira club has the following number of goals scored against them, 0,1,0,2,9,0,1,2,1, what is the mean number of goals scored against them?
(b)The table below shows the masses of 100 students to the nearest kg
| Mass kg | 60-62 | 63-65 | 66-68 | 69-71 | 72-74 |
| Frequency | 5 | 18 | 42 | 27 | 8 |
- Determine the mean of the masses
- Calculate the mode
- Draw a cumulative frequency (give) curve and use it to determine the median of the masses
12.(a)(i) Find the distance between Mbeya (9°S.33°E) and Tabora (5°S,33°E) in km
(b)An airplane takes off from Tabora (5°S,33°E) to Tanga (5°S,39°E) at a speed of 332 kmh-1 if it leaves Tabora at 3:00pm, at what time will it arrive at Tanga airport?
13.Musa started business on 1st June, 1999 with Tshs 6000/= as capital
June 01 Bought goods cash 3000/=
June 02 Paid office cleaners 20/=
June 03 Sold all goods for cash 3400/=
June 05 Purchased goods for cash 2000/=
June 08 Paid carriage on goods sold 40/=
June 10 sold goods for cash 3000/=
June 15 paid wages 100/=
- Enter these transactions in cash book
- Bring down the balance at the end of June
14. A house and flag post are on the ground. From an open window in a house 6m, above the ground, Abdulrazaq finds that the angle of elevation of the top of the flag post is 35° and the angle of depression of the bottom of the flag post is 20°.
15.(a) Draw the graph of ![]() taking the value of x in the interval
taking the value of x in the interval ![]()
(b)State the running point of the graph and state whether it is a maximum or a minimum.
(c)Solve the equation ![]()
(d)Use a suitable straight line, solve the equation ![]()
16. (a). Box A contains 8 items of which 3 are defective and box B contains 5 items of which 2 are defective. An item is drawn at randomly from each box. What is the probability that?
- Both items are non-defective?
- One item is defective and one item is not defective
(b)The radii of trastrom of a right cicular cone are 10cm and 7cm. If the height of this trastrom is 6cm. What will be the height of the original cone?
(c)If ![]()
- Find an expression for
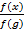
- Find the simplified algebraic expression for f(x-1)
FORM THREE MATHEMATICS EXAM SERIES 88
FORM THREE MATHEMATICS EXAM SERIES 88
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM 3 BASIC MATHEMATICS
SECTION A (60 MARKS)
Answer ALL questions from this section
1(a) Write 0.007357 correct to three significant figures
(b)Express ![]() inform
inform ![]() where
where ![]()
(c)Simplify ![]() hence write your answer in percentage.
hence write your answer in percentage.
2.(a)Solve for x in the following equation ![]()
(b)Rationalize the denominator ![]()
3(a)In a school of 200 students 90like mangoes, 70 like oranges and 50 like Apples; 26 like oranges and mangoes, 20like oranges and apples, 16like Apples and mangoes while 10 like all three fruits.
Represent this information in a well labeled Venn diagram
How many students do not like mangoes?
(b)If ![]() , Find b in terms of A and C
, Find b in terms of A and C
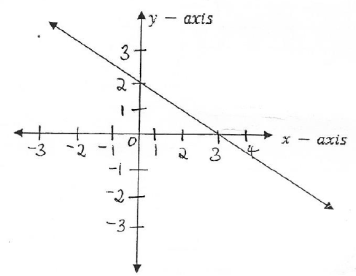
4. Use the graph below, then find;
Gradient
Equation of the line in the form of y=mx + c
5.(a)ABC is an isosceles triangle in which![]() and
and ![]() are equal and if D is the mid-point of BC.
are equal and if D is the mid-point of BC.
Prove that ![]()
(b)A regular polygon has an exterior angle of 72° find
- The size of the interior angle
- How many sides does this polygon have?
6.(a) If y varies directly as x2 and inversely as ![]() when x=8, y=16 and z=25.
when x=8, y=16 and z=25.
Find y when x=5 and z=9
(b)Sixty people working 8 hours a day take 4 days to cultivate a village farm. How long will it take twenty people to cultivate the same farm if they work 15 hours a day?
7(a)Three people share a property in a ratio 2:x:y. It is known that y=x +2, if the largest shareholder had shs 780,000/= in monetary terms, find the value of this property.
(b)Mr.Mayube of Makole village shop made 60% loss by selling a bag of sugar for Shs. 80,000.00. What would be his percentage profit if he sold the bag of sugar for Shs 240,000.00?
8(a)Write down the next two terms in the sequence; ![]()
(b)The first four terms of an A.P are 2,(m – n), (2m + n + 7 and (m – 3n) respectively where m and n are constants. Find the values of constant m and n
9(a)Given that Tan A=2.4 and A is an acute angle. Find in the simplified form the value of ![]()
(b)From the top of a wall 8.8m above horizontal ground, the angle of depression of a stone lying on the ground 31°. Calculate the distance of the stone from the foot of the wall.
10(a)Find the factors ![]() and hence use it to solve
and hence use it to solve ![]()
(b)The operation x*y denotes the number. Find the value of x if x*4=x*3
SECTION B –(40 MARKS)
Answer any four (4) questions from this section
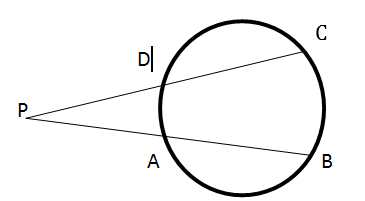
11.(a)In the following figure ![]() shorter than
shorter than ![]() . Find the length of
. Find the length of ![]()
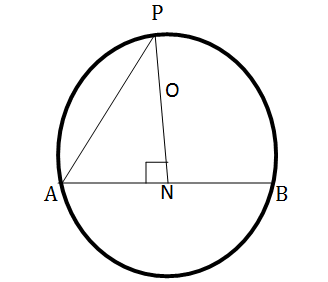
(b)In figure below O in the center of the circle. AB=6cm and ON=4cm show that ![]()
12. The score of 50 candidates a mathematics examination were recorded as shown below.
26, 17, 42, 40, 40, 74, 26, 34, 34, 47, 52, 42, 69, 52, 43
67, 38, 52, 24, 34, 48, 73, 64, 55, 43, 67, 38, 56, 18, 53, 26
62, 32, 78, 17, 45, 34, 54, 24, 36, 34, 18, 48, 52, 73, 37, 64, 45, 54, 37
- Prepare a frequency distribution table with class mark 17, 22, 27 …………
- Draw histogram and use it to estimate mode
- Calculate mean, using assumed mean of 52
13.(a)Find the distance between A(20°N, 135°E) and B (35°N, 135°E) in
(i)Nautical miles (ii) Kilometer
(b)A ship sails from P(0°, 30°W) to Q(10°N, 30°W) at 15 knots. If it leaves P at 8:00am on Tuesday when will reach Q?
14.You are required to use the trial balance below to prepare trading, profit and loss Account and extract the balance sheet of Mwanahela as at 31-12-2012
| S/NO | NAME OF ACCOUNT | DR | CR |
| Cash | 1,907,000 | ||
| Capital | 2675000 | ||
| Purchases | 2267000 | ||
| Rent | 114000 | ||
| Furniture | 305000 | ||
| Shelves | 270000 | ||
| Sales | 2309000 | ||
| Salary | 67000 | ||
| Wages | 54000 | ||
| 4984000 | 4984000 |
15.(a)The sum of the first three terms of a geometric progression is 19 and their product is 216. Find the terms
(b)The third term of an arithmetic progression 9 and the common difference in 2. Find the sum of the first 20terms.
(c)If p, q and r are successive terms of a geometric progression. Find the value of q in terms of
p and r
16.Given that 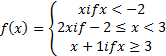
- Sketch the graph of f(x)
- State the domain and range of f(x)
- Find f(-5), f(10), f(3?) and f(0)
- Is f(x) one to one to one function?
1
FORM THREE MATHEMATICS EXAM SERIES 81
FORM THREE MATHEMATICS EXAM SERIES 81
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
FORM III BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 3 Hours Year: 2021
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions.
2.Answer all questions in sections A and B.
3.Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
5.NECTA mathematical tables and non-programmable calculator may be used.
6. All communication devices and any unauthorized materials are not allowed in the examination room.
SECTION A (60 MARKS)
1.(a) Express the numbers 1470 and 7056 each as a product of its prime factors.
Hence evaluate and simplify
![]()
if m = 1470 and n = 7056.
(b)Express 0.00152 correct to: (i) two (2) significant figures
(ii)three (3) decimal places
(iii)in standard form
2.(a) Express x and y into fraction and hence find x + y, given that
![]() and
and ![]()
(b)Solve for x in the following equation
![]()
3.(a) Solve for n
![]()
(b) Given that x2 + 8x +Q = (x + K)2
4 .In a certain school, 40 students were asked about whether they like tennis or football or both. It was found that the number of students who like both tennis and football was three times the number of students who like tennis only. Furthermore, the number of students who like football only was 6 more than twice the number of students who like tennis only. However, 4 students like neither tennis nor football.
(a)Represent this information in a Venn diagram, letting x be the number of students who like tennis only.
(b)Use the results obtained in part (a) to determine number of students who likes;
(i)Football only.
(ii)Both football and tennis.
5.(a) Find the equation of the line through the point (2,?2) crossing the ![]() -axis at the same point as the line whose equation is y=2x- 4
-axis at the same point as the line whose equation is y=2x- 4
(b) Express y in terms of x; 3x + 2y = 6 and Without drawing the graph, state the gradient, the y – intercept and x – intercept in the equation.
6.(a) The length of a rectangular field is 20m longer than the width. Find an expression for the perimeter of the field in terms of its length.
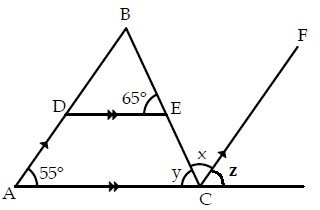
(b) In the figure below, Find angle x, y and z
7.(a) The parallel sides of a trapezium are 8cm and 12cm respectively. If the distance between the parallel sides is 9cm, calculate its area.
(b) A lady buys a printer for sh.26000 and when she sells it she realizes a loss of 40%. How much did she sell the printer for?
8. (a) If y2 varies directly as x-1 and inversely as x+d and if x=2, d=4 for y=1, then find x when y=2 and d=1.
(b)If 8 students in a typing pool can type 210 pages in 3 days, how many students will be needed to type 700 pages in 2 days?
9.(a) If ![]()
Find
i) Cos A
(ii)
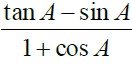
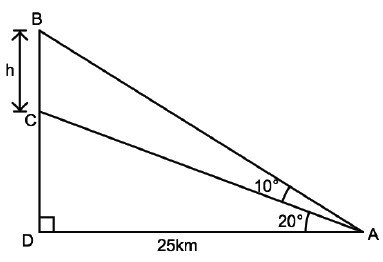
(b) Given the following figure, find the value of h, correct to one decimal place
10.(a)Compute the sum of the first ten terms of the series 1+5+9+....
(b)The 5th term of A.P is 23 and the 12th term is 37. Find
(i)The eleventh term
(ii)The sum of the first eleventh terms by using the values computed above without using the common difference for this progression.
SECTION B(40%)
Answer All Questions In This Section
11.Given the relation;
![]()
(i)Sketch the graph of R.
(ii)State its domain and range.
(iii)Find inverse of relation R
12. Given that
![]()
(a) (i) Sketch the graph of f(x)
(ii) State its domain and range (iii) Is f(x) a one - to – one function?
(b) Find:
( i ) f(-4)
( ii ) f(2)
( iii ) ![]()
![]()
![]()
![]()
13. The masses of 40 parcels handled at transport office were recorded as shown in table below
| Mass(kg) | 1.0- 1.9 | 2.0-2.9 | 3.0-3.9 | 4.0 - 4.9 | 5.0 - 5.9 | 6.0 - 6.9 |
| Number Of Parcels | 6 | 2x | 10 | x | 2 | 1 |
a)Find value of x
b)Determine modal class and its corresponding class mark
c)Find Median
14.( a) Given f(x) = x2 - 4x + 2. Find
i) Axis of symmetry ii) Maximum or minimum value
iii) Turning point
(b)Draw the graph of f(x) in 14(a) and use it to solve the equation x2 - 4x -2 =3
FORM THREE MATHEMATICS EXAM SERIES 56
FORM THREE MATHEMATICS EXAM SERIES 56
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
BASIC MATHEMATICS TERMINAL EXAMINATION-MAY
FORM THREE
Time 3:00 Hours MAY 2020
Instructions
- This paper consists of two sections A and B.
- Answer all questions in Section A and only four questions in section B
- Show clearly all working for each question
- Mathematical tables, geometrical instruments and graph paper may be used where necessary
SECTION A (60 MARKS)
1. (a) Arrange the number ![]() in ascending order.
in ascending order.
(b) Express 0.06896 correct to:
(i) three (3) significant figures
(ii) three (3) decimal places
(iii) in standard form
2. (a) Solve for x in the equation: 32x-3 x 8x+4 = 64 ÷ 2x
(b) Solve for x in the equation log(x2+8) – logx = log6
3. (a) Find the solution set of the inequality ![]() and indicate it on a number line.
and indicate it on a number line.
(b) If ![]() find n if
find n if ![]()
(c) Simplify the following expression and state the coefficient of ![]()
![]()
4. (a) In a school of 75 pupils, 42% of the pupils take Biology but not Chemistry, 32% take both subject and 10% of them take Chemistry but not Biology. How many pupils do not take either Biology or Chemistry?
( b) The Venn diagram below shows the universal set U and its two subsets A and B
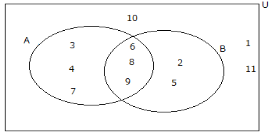 Write down the elements of
Write down the elements of
i) A’ ii)B’ iii)AUB iv) A’UB’
5. The figure ABCD below is rectangle with sides as shown where C1 and C2 are two quarter circles inside it.
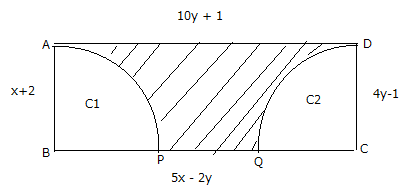
Find:
a) Value x and y shown in the figure above
b) Perimeter of the rectangle
c)Area of the rectangle ABCD
d) Area of the shaded region
6. (a) The variable v varies directly as the square of x and inversely as y. Find v when x = 5 and y = 2; given that when v = 18 and x = 3 the value of y = 4.
(b) The temperature (Ti) inside a house is directly proportional to the temperature (to) outside the house and is inversely proportional to the thickness (t) of the house wall. If
Ti = 320C when To =240C and t = 9 cm, find the value of t when Ti = 360C and To = 180C
7. (a) A shirt whose marked price is Tshs 80,000/= is sold at a 13% discount, if the trader makes a profit of 20%, find the selling price of the shirt.
(b) A regular polygon has an exterior angle of 360
- Find the size of the interior angle
- How many sides does this polygon have
- Find the sum of interior angles of this polygon
8. (a) Find the 10th term of the G.P if the 4th term is 8 and the 7th term of this G.P is 16.
(b) Find the sum of the first 10 terms of the series: 4 + 6 + 8 + - - - - - - - -
9. (a)Find the value of ![]() without using mathematical tables.
without using mathematical tables.
(b) A ladder leans against vertical wall. If the ladder reaches 12m up the wall and its foot is 9 cm from the base of the wall. Find the length of the ladder.
10. (a) Factorize completely ![]() by splitting the middle term
by splitting the middle term
(b) Factorize ![]() and hence find exact value of (10003)2 –(997)2
and hence find exact value of (10003)2 –(997)2
(c) Solve the equation ![]()
SECTION B ( 40 MARKS )
(a) The function f is defined as follows:
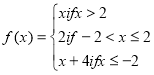
(i) Sketch the graph of ![]() .
.
(ii) Determine the domain and range of ![]()
(b) If R-1 =![]() . Find the domain and range of R
. Find the domain and range of R
12. The 4th, 6th and 9th terms of arithmetic progression forms first three terms of geometric progression. If the first term of the A.P is 3, determine the:
(a) Common difference of the arithmetic progression
(b)Common ratio of the geometric progression
(c) Kicheche deposited Tshs100000/= in a bank at a compound interest of 8% per annum for 4 years. Find how much interest he received
13. The weight in kg of 40 students were recorded as follows:
| Weight in(kg) | 10 - 19 | 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | 60 - 69 | 70 - 79 |
| Number of students | 8 | 3 | x | 8 | 7 | 2 | 2 |
Calculate:
(a) The value of x
(b) The mode by using the formula.
(c) By using an assumed mean, find the average weight of the students
(d) Draw a cumulative frequency curve and hence use it to estimate median.
14. a) A farmer sold a quarter of his maize harvest and give one third of the remaining to his relatives. If the farmer remained with 36 bags of maize, find:-
i) How many bags of maize did the farmer harvest.
ii) How many bags of maize did the farmer sold.
b)A shopkeeper makes a profit of 20% by selling a TV for 480,000/=
i) Find ratio of buying to selling price
ii) If the radio would be sold for 360,000/=, what would be the percentage loss?
15. The function f is defined as follows:
f(x) = 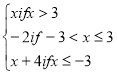
![]()
i) Sketch the graph of f(x)
ii) Determine domain and range
iii) Find i) f(0) ii) f(-6) iii) f(π)
b)For what values of x is fuction f(x)=![]() is undefined?
is undefined?
16. Mr. Chakubanga started business on 15th February, 2005 with capital in cash 1,055,000/=
February 16 Bought goods for cash 500,000/=
18 Bought shelves for cash 55,000/=
19 Sold goods for cash 450,000/=
20 Purchases for cash 400,000/=
21 Sold goods for cash 700,000/=
25 Paid rent for cash 150,000/=
Required: Record the above transactions in the respective ledgers and extract a trial balance.
FORM THREE MATHEMATICS EXAM SERIES 21
FORM THREE MATHEMATICS EXAM SERIES 21
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256