WAVES

 The student should be able to:

 Explain the concept of a wave;

 Explain the terms wave long frequency and velocity of a wave; and

 Identify types of waves.

 Explain the term refraction, reflection, diffraction and interference of a wave

 Mention the applications of refraction, reflection, diffraction and interference of a wave in daily life

 Demonstrate the behaviour of waves

 Describe the propagation of mechanical waves.

 Explain the propagation of electomagnetic waves

 Determine the relation between frequency, speed and wavelength of a wave and determine the refractive index of a medium

 Identify the sources of sound waves

 Explain the concept of audability of sound

 Describe the perception of hearing

 Explain the concept of echo and reverbaration of sound.

 Explain concept of a musical sound;

 Identify factors affecting loudness, pitch and quality of a musical sound.

 Identify the different musical instruments

 Explain the terms stationery wave, nodes and antinodes

 Determine the frequency of a musical note

 Differentiate between fundamental note and overtones

 Explain the concept of resonance as applied in sound waves

 Construct a simple musical instrument.

 Explain the concept of the electromagnetic spectrum

 Identify the main bands of the electromagnetic spectrum

 Detect infra-red, visible and ultra violet rays

Wave is a progressive disturbance propagated from a point in a medium (matter) on space without the movement of the points themselves. For Example, light, sound and water waves

Terms Used

• Period: period is the time taken for complete a cycle. It represented by letter T. it SI unit is second (s)
• Amplitude: Amplitude is the maximum displacement of the wave from the equilibrium position. It represented by letter A. it SI unit is metre (m)
• 5Crest: Crest is the point of maximum positive displacement of the wave from the equilibrium position.
• Trough: Trough is the point of maximum negative displacement of the wave from the equilibrium position.
• Wavelength: Wavelength is the distance between two successive or adjacent crests or troughs. It
  represented by letter Lambda (A)

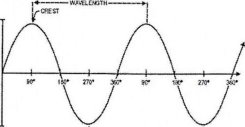
• Frequency: Frequency is the number of crest or trough that passes a given point per unit time. It represented by letter f . Its SI unit is 1 hertz (Hz) = 1 per second (s^-1)

Mathematically: = f= 1/T

Wave velocity: Wave velocity is the speed at which the wave moves through a medium.

Or

Wave velocity is the displacement of the wave per unit time. It represented by letter v.

Mathematically;

V = λ/T = λ x 1/T

But: ƒ= 1/T

V=λxf = λƒ

V=λƒ

Example,

From the diagram below, determine the amplitude, period and frequency of the wave.

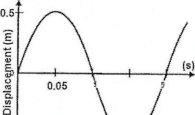
-0.5

Solution

From the graph

Amplitude, A = 0.5m

Period, T = 0.2

Frequency, f = 1 /T = 1 /0.2 = 5Hz

Example,

From the diagram below, determine the wavelength and velocity of the wave, frequency of the wave is 5Hz

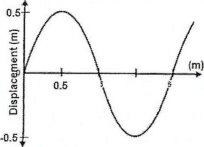
Solution

From the graph

Wavelength, A = 2m Velocity, v = ?

But: Frequency, f = 5Hz

From: V = λf

Then: V = 2 x 5 = 10m/s
V = 10m/s

Types of Waves

There are two types include

• Electromagnetic wave
• Mechanical wave

Electromagnetic Wave

Electromagnetic wave is the kind of waves in which it does not require a medium to transfer energy.

Properties of Electromagnetic Wave

• The disturbance made up of electric and magnetic fields
• can travel through vacuum

Example, visible light and sun rays.

Mechanical Wave

Mechanical wave is the kind of waves in which require a medium to transfer energy.

Properties of Mechanical Wave

• mechanical travel through a medium the particle that make up the medium are disturbed from their rest or equilibrium position
• can travel through medium
• Example, sound wave.

Types of Mechanical Waves.

There are two types which includes

• Transverse wave
• Longitudinal wave

Transverse Wave

Transverse wave is the mechanical wave in which particles of the medium vibrate in a direction perpendicular to the direction of movement of the wave. For Example, water wave.

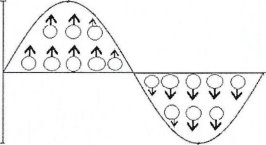
This vibration of medium cause boat on the ocean moves up and down while the waves themselves move toward the shore.

Longitudinal Wave

longitudinal wave is the mechanical wave in which particles of the medium vibrate in a direction parallel to the direction of movement of the wave. For Example, sound wave.

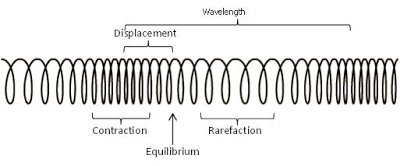
It consist compression where the particles packed closely together and rarefactions where the particles are spread out

Behaviour/Properties of Waves

If waves travel from one to another point it may the following characteristics

 Reflection of waves

 Refraction of waves

 Interference of waves.

 Diffraction of waves

Reflection of Waves

When wave encounter a boundary through which it cannot pass it will be reflected. If boundary fixed the reflection is inverted.

If the wave travel from less denser medium to denser medium the reflection will inverted.

Inverted reflected wave Transmitted wave.

If the wave travel from denser medium to less denser medium the reflection will not inverted.

LAWS OF REFLECTION OF WAVES.

The laws of reflection of waves states that

1st. "the incident direction of propagation, the reflected direction of propagation and
the normal all lie in the same plane"

2nd."The angle of incidence equals to the angle of reflection"

NB:

• Direction of waves is represented by an arrow called a ray which drawn perpendicular to wave fronts in straight surface
• If water waves encounter an parabolic (concave/convex) Barrier the waves

Applications of Reflection of Waves

• Reflection of light waves is used in the designing of plane mirror
• Reflection of waves (sound waves) used on measuring distance

• .Sonar system rely on the reflection of sound waves to assist ships in navigating, communicating and detect other vessels

Ripple Tank Experiment

Ripple tank experiment consists of water pool in shallow rectangular dish with a clear glass base, wooden/metal bar for generating water waves

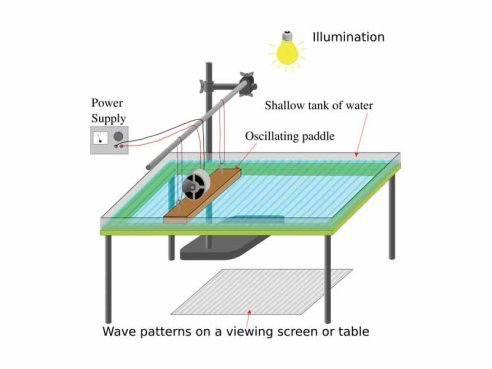
Main Parts of Ripple Tank

The basic components of ripple tank experiment are ripple tank, water, power supply, stroboscope, electric motor, wooden bar (vibrator), bulb and white board or white sheet (screen)

• metal bar (wooden bar)
• Shallow tank of water
• Motor
• Oscillating paddle
• Lamp
• Paper sheet
• Various obstacles. E.g. Laying glass
• stroboscope

Metal bar

A metal bar (wooden bar) is screwed to the electric motor and suspended above the ripple tank with rubber (elastic) bands and touching the water surface.

Shallow tank of water

Shallow tank of water is the source of waves in which an oscillating paddle generates parallel water waves

Motor

The rotating armature (axle) of an electric motor makes the wooden/metal bar to vibrate on water surface and generating ripples

Oscillating paddle

Oscillating paddle is the one in which transform mechanical energy generated by motor by off centre mass to wave energy in a Shallow tank of water

Lamp/ Bulb/ filament

Bulb or filament which used to illuminate the water surface to see the water waves onto the white board or white sheet below the ripple tank.

Paper sheet

Paper sheet used to display shadow of the wave pattern placed under the tank.

Various obstacles

Various obstacles is paced in the tray to observe properties of waves e.g. reflection, refraction, interference and diffraction. Example, laying glass,

Rectangular, barrier, curved,barrier
(concave and convex barrier) etc

Stroboscope

The stroboscope enables the observer to see the waves as stationary

Laying glass

Laying glass used to vary the depth (tray thickness) of the water. This allows observing waves travelling from one to another medium

Power supply

Power supply for electric motor

Refraction of Waves

Refraction of waves involves a change in direction of waves as they travel from one
to another medium due to a chance in speed (v) and wave length (A). It obey Snells law

Diagram:

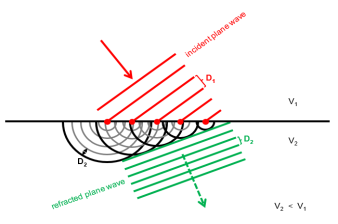
NB:

(a) When wave is refracted into an less media, The frequency of wave increases and vice versa

(b) When wave is refracted into an less median The speed of wave increases and vice versa

(c) When wave is refracted into an less median the wave length of wave increases and vice versa

(d) When wave is refracted into an less median The wavelength of wave does not change (unaltered) and vice versa

Application of Refraction of Waves

 It is used in optical instruments which focus or spread light. For Example, microscopes and telescopes

 It is used in dispersion of light waves.

 lt is used to determine the eyes refractive error

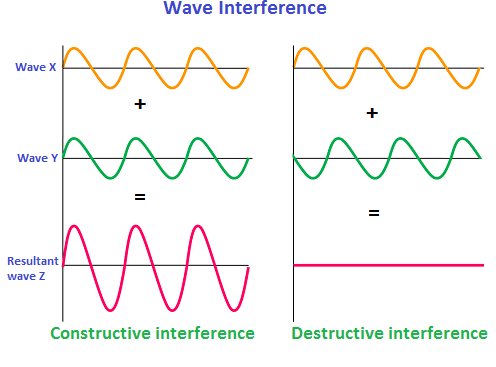
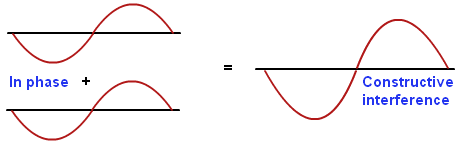
Interference of Waves

Interference of waves involves meets of two or more waves. Interference also known as addition/superposition which result a new wave pattern.

Principle of Superposition

It states that

"The resultant displacement at any points is equal to the sum of the displacements

of different waves at the point"

Nb:

 When two different crests meet at the same point in the same direction results greater amplitude than individual, this refers as constructive interference.

 When crest and trough meet at the same point in the opposite direction results smaller amplitude than individual, this refers as destructive interference

iii. Consider the table below.

Wave A amplitude	Wave B amplitude	resultant amplitude
+1	+1	+2
+2	-1	+1
-1	+1	0
+1	-2	-1
-1	-1	-2

 When waves interfere, the lines of increase disturbance (constructive interference) is called antinodal lines while When waves interfere, the lines of zero disturbance,(destructive interference) is called nodal lines.

Diagram:

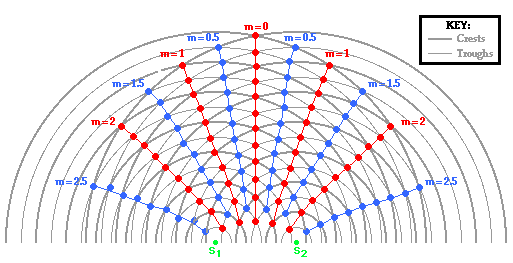
Where:

S1= first wave source

S2= second wave source

Dark circle = crest meet crest Blank circle = trough meet trough Half-dark = crest meet trough

Blue (Lines) = antinodal

Red (Lines) = nodal

Application of Wave Interference

• Creation of hologram. holograph is a photograph of an interference pattern which is able to produce a three dimensional image when suitably illuminated
• Noise reduction system. For Example, earphones capture environment sound which destructed by second computer sound.
• Concert and auditoriums designed to reduce destruction interference by introduce sound absorber

Diffraction of Waves

Wave diffraction is the apparent bend when encounter an obstacle and spread out of wave when they go through a gap.

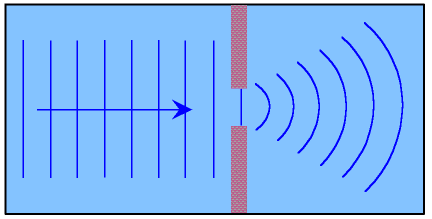
Nb:

• The gap is inversely proportional to wave diffraction (spreading), small the width of gape the large wave diffraction (spreading)

• Diffraction of wave is greater when the wave length and width of gap is the same
• We hear someone sound even she/he behind the building due to diffraction of wave sound

Characteristics of Diffracted Wave

• Wavelength does not change.
• Frequency does not change.
• Speed of diffracted does not change.
• The amplitude of the wave decreases after diffraction.

Factors Affecting Diffraction

The magnitude of diffraction (or angle of diffraction) depends on

• The wavelength
• The size of the opening gap

Applications of Diffraction Of Wave

• It is used in determine the crystal structure of materials
• It is used in measuring the coefficient of thermal expansion, crystalline size and thick of thickness of thin films.
• lt is used in determine the types and phases present in a specimen where the spacing of obstacles (atoms) is between 1 and 3nm

Sound Waves

Sound wave is a longitudinal wave that produced by vibrating object. For Example, turning fork.

Propagation of Sound Wave

Sound travels by vibrating of particles to transfer energy to the next particle until the sound reaches another point.

Question: why solid materials transfer sound faster than liquid/gas

Answer: the molecules/particles of solid materials are packed together

Sources of Sound Wave

Almost everything ranging from people, animals, plants and machines

Musical Instruments

Musical instrument is designed to produce specific types of sounds include guitars, violins, organs, recorders, flutes, drums, marimbas.

Factors Affect Speed of Sound In Air.

Speeds of sound can be affected by the following factors

 Temperature

 Direction of wind

 Humidity

 Density of air

Temperature

Sound is the form of kinetic energy. Molecules at higher temperature have more energy, thus they can vibrate faster so sound waves can travel more quickly.

Direction of Wind

Sound will travel faster toward direction of wind while in opposite direction the speed of sound decreased

Wind direction: V α W

Wind in opposite direction: V α

Humidity

Sound is the form of kinetic energy. Molecules at low temperature (humidity) have lower energy, thus they can vibrate slowly so the speed of sound decreased.

Density of Air

Increase in temperature tend to decrease the density of air so increase in density of air tend to decrease speed of sound in air.

Audibility Range

Audibility range is the range of frequency detected by ear.

Nb:

• The ear is most sensitive to sound with a frequency around 3000Hz
• Sound below 20Hz is called Infrasonic sound.

Audio Range Table

Animal	Audio range (Hz)
Chicken	125 - 2000
Penguin	100 - 15000
Owl	200 - 1 2000
Cattle	23 - 35000
Sheep	100 - 30000
Dog	67 - 45000
Cat	45 - 64000
Rabbit	360 - 42000
Horse	55 - 33500
Rat	500 - 64000
Blue whale	5 - 12000
Rissos dolphin	8000 - 100000

The human ear.

An organ responsible for conversion of sound energy into mechanical energy and to nerve impulse transmitted to brain for interpretation. It can distinguish amplitude, direction and frequency

Part of Human Ear

It consists three basic parts include

• outer ear
• Middle ear
• Inner ear

Inner ear consists of the cochlea, semicircular canals and the auditory nerve.

• Cochlea

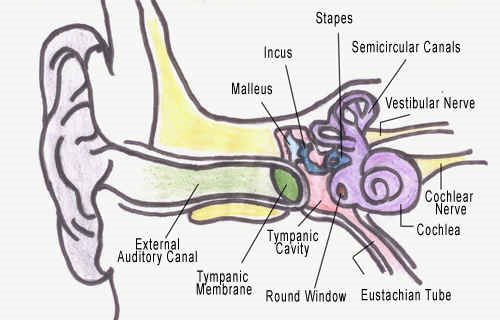
Outer ear consist earflap and the ear canal. Sound reach outer ear in the form of pressure with an alternating pattern of high and low pressure regions.

Middle Ear

Middle ear is air filled cavity that consists of an ear drum and three small interconnected bones Hammer, anvil and stirrup. Eustachian tube connect mouth and middle for regulation of pressure.

Inner Ear

Chochlea

Cochlea is the auditory portion of the inner ear. It consist nerves called cochlea nerve or auditory nerve or acoustic nerve. Auditory nerves are differ in length for unique natural sensitive to particular frequency of vibration

Semicircular Canals

Semicircular canal is filled with fluid known as endolympth. It have nerve which responsible for balancing the body.

Mechanism of Hearing

Earflap collect sound wave, which pass through the ear canal to hit drum which results vibration of interconnected bones where vibrate cochlea fluid through (oval window) results vibration of hair cells which transform mechanical energy to electrical impulse, which transmitted to the brain where they are decoded and interpreted as sound

Echo

echo is the reflected sound when then encounter an obstacle. Since the sound waves goes and bounce back it distance becomes 2d.

Hence speed (v) of sound associated with echo is calculated by

v = 2d/t

Nb:

• Always echo reaches the ear more than 0.1s
• At 25⁰C the speed of sound in air is 340m/s
• From: v = 2d/t

Then: 2d=vxt= 0.1 x340

d = 17m

Therefore: minimum distance an obstacle kept is 17m for echo to be heard.

Reverberation

Reverberation is reechoed sound

Example,

A gun was fired and the echo from a cliff was heard 8s later. How far was the gun from the cliff?

Data given

Time taken by echo, t = 8s

Wave velocity in air, v =

Distance moved by sound, 2d = ?

Solution

From: d = v x t

2d = 1500 x 8

2d = 2800m

d= 1400m

Example : NECTA 2000, QN: 04

• Define an echo
• Name any two factors that affect the speed of sound in air
• Explain briefly why sound produced in hall with many people is heard more clearly than when the hall has few people?
• A person standing 99m from the foot of mountains claps his hands and hears an echo 0.6 second later. Calculate the speed of the sound in the air.

Solution

(c) When a hail has many people, most of the sound (including echoes) is absorbed by clothes and skins of the audience, thus echoes do not occur

Data given

Wave distance, d = 99m

Echo time, t = 0.6s

Sound speed, v = ?

Solution

From: v = 2d/t

v = 2d/t = (2 x 99)/0.6 = 198/0.6 = 330 v = 330m/s

Uses of Echo

Under water echo is used

• To find depth of ocean/ocean
• To detect the submarines.
• To detect large groups of fish.
• To detect the wrecked ships.
• To detect the dangerous rocks

Musical Sounds

Musical sound is the sound musical scale (combination of frequencies) that appealing the human ear

Noise

Noise is the random and non-structured sound musical scale (combination of frequencies) that not appealing to the human ear

Properties of Musical Sounds

The follows is the properties used to describe musical sounds, include

• Loudness
• Pitch
• timbre

Loudness

Loudness is the intensity of the sound as perceived by the human ear. The large the amplitude, the louder the sound.

Pitch

Pitch is a property of sound to which sound can be ordered to scale from high to low. The higher the frequency, the higher the pith produced.

Timbre

Timbre is the quality/colour of sound produced by an instrument. For Example, different instrument produce different sound.

Musical Instruments

Musical instruments are a device constructed/modified for making music.

Category of Musical Instrument

It categories into three groups include

• String instrument
• Percussion instrument
• Wind instrument

String Instrument

String instrument is the instrument produced sound by stretched plunked/bowed/struck string. Example, guitar is plunked, violin is bowed and piano is struck

Percussion Instrument.

Percussion instrument is the instrument produced sound by struck with implement/shaken/rubbed or scrapped. Example, drum, cymbals, tambourine, marimba and xylophone.

Wind Instrument

Wind instrument is the instrument produced sound by blowing. Example, recorders, flutes, vuvuzela and trumpets.

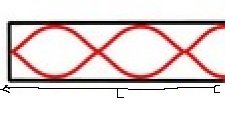
Stationary Waves

A stationary wave is the result when two wave waves travel in opposite direction with the same speed and frequency superposed.

Diagram: crest and trough meet.

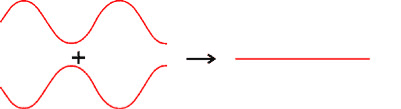
Diagram: crest/trough and crest/trough meet.

NB:

i. In string waves their amplitude are alternate between adding together and cancelling

Diagram:

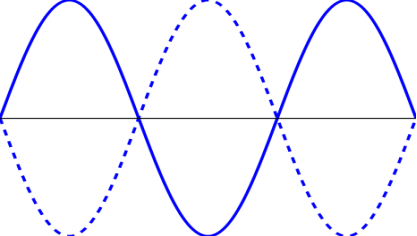
2. When adding together producing maximum displacement (amplitude) called antinodes.
3. When cancel out producing zero displacement (amplitude) called nodes
4. Distance between adjacent antinodes is equal to half wave length, L = A/2
5. Distance between adjacent nodes is equal to half wave length, L = A/2vi. distance between a nodes and an adjacent antinodes equal to one quarter, L = A/4

Fundamental Frequency

Fundamental frequency is the lowest frequency of a vibrating object

Fundamental Note

Fundamental note is the note respond to Fundamental frequency

Fundamental Harmonic

A harmonic is defined as an integer (whole number) multiple of the fundamental frequency

Fundamental Overtones

Fundamental overtones is any frequency higher than the fundamental frequency

NB:

1. The fundamental note is equal to first harmonic
2. The second harmonic is equal to first overtone
3. Stationary wave in string have certain fixed wavelength

Consider the diagram below fundamental note

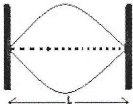
From: L = λ/2 Also: λ = 2L From: V = λƒ Then: V = 2Lƒ1

Diagram: second harmonic

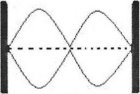
From: L = 2λ/2

Also: λ = 2L/2 From: V = λf2

Then: V = (2Lf2)/2 = Lf2

Diagram: third harmonic

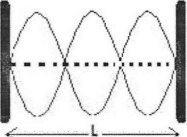
From: L = 3λ/2 Also: λ = 2L/3 From: V = λf3 Then: V = (2Lf3)/3

Generally

From: V = (2Lf3)/3

Three represent the third series of harmonic therefore the formula modified to

V = (2Lf_n)/n

Where:

n = nth harmonic

f = frequency

v = wave velocity

L = length of string

f_n = frequency of nth harmonic
f = frequency of 1 th harmonic

f2 = frequency of ^2nd harmonic

f3 = frequency of 3^rd harmonic

Sonometer

Sonometer is an instrument used to study properties of stationary wave.

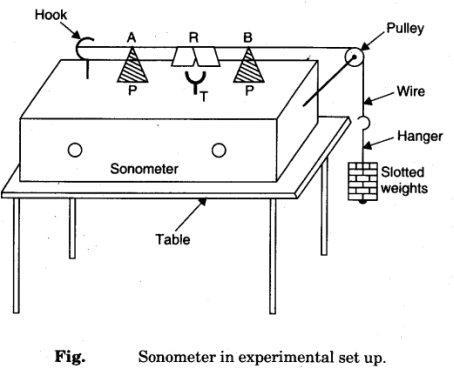
Factors Affect the String Frequency

There are three factors that affect the frequency of vibrating wire, include

• Length of wire, L
• Tension of the wire, T
• Mass per unit length, p

Length of Wire

The frequency is inversely proportional to the length of wire.

Ƒα1/L……………1

Tension of the Wire

The frequency is directly proportional to the square root of wire tension

ƒα√T……………….2

Mass per Unit Length

The frequency is directly proportional to the square root of mass per unit length

ƒα√1/µ………………..3

Combine three equations

Ƒα1/L√T/µ

- Remove proportionality constant

Ƒ=k1/L√T/µ

WERE k =1/2

Ten; Ƒ=1/21/L√T/µ

Ƒ=1/2x1/L√T/µ

Ƒ=1/2L√T/µ

From: V = (2Lfn)/n make f subject

Ƒ=vn/2L = 1n/2LXV

By compassion

Modify formula

Since: µ =m/l substitute in equation above

Ƒn=n1/2l√LT/m

Where:

n = n^th harmonic

fn = frequency of n^th harmonic

Example,

A string has a length of 75cm and a mass of 8.2g, the tension in the string is 18N. Calculate the 1st harmonic and 3rd harmonic.

Data given

Length of string, L = 75cm = 0.75m

Mass of string, M = 8.2g = 0.0082kg

Tension of string, T = 18N

1st harmonic, ƒ1 = ?

3^rd harmonic, ƒ3 = ?

Solution

From: f_n = Ƒn=n1/2l√LT/m

1st harmonic, fi = ?

Ƒn=1x1/20.75√0.75x18/0.0082 =27

fi = 27Hz

3^rd harmonic, ƒ3 = ?

Ƒn=3x1/20.75√0.75x18/0.0082 =81

ƒ3 = 81Hz

Example,

The vibration length of a stretched wire is altered at constant tension until the wire oscillates in unison with a turning fork of frequency 320 Hz. The length of a wire is again altered until it oscillates in unison with a fork of unknown frequency. If the two lengths are 90 cm and 65.5 cm, respectively, determine the unknown frequency.

Data given

1st Length of string, Li = 90cm = 0.9m

2ⁿd Length of string, L2 = 65.5cm = 0.655m 1st harmonic, ƒi = 320 Hz

2nd harmonic, ƒ2 = ?

Solution

From: f α1/L

Then: fL= K

Finally: ƒ1L1 = f2L2- make f2 subject ƒ2= (111_1)/LI

12= (320 x 0.9)/0.655 = 440 Hz

f 2 = 440 Hz

Example, NECTA 1995: QN 08

A Sonometer wire of length 40cm between two bridges produces a note of 512Hz when plucked at the midpoint. Calculate the length of the wire that would produce a note of 256Hz with the same tension

Data given

1st Length of string, Li = 40cm = 0.4m 1st harmonic, fi = 512Hz

2^nd harmonic, f2 = 256Hz

2^nd Length of string, L2 = ?

Solution

From: f α1/L

Then: fL= K

Finally: f i Li = f2L2- make L2 subject L2⁼ (fl Li)/f 2

f2 = (512 x 0.4)/256 = 0.8m L2= 0.8m

Forced Vibration and Resonance

Forced Vibration

Forced vibration is the vibration in a system as a result of impulse received from another system vibrating nearby.

RESONANCE

Resonance is the tendency of a system to oscillate at maximum amplitude at certain frequencies from another system. For Example, turning fork can produce resonance on a piece of wood.

Nb:

Frequency of vibration is equal to the frequency of turning fork (the one cause resonance)

Resonance in Closed Pipe

Consider the diagram below

Diagram:

Where:

c = end correction

L = λ/4

From: L = λ/4 - without end correction L + c = 3λ/4 - with end correction

Diagram: second harmonic/resonance

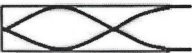
From: L = 3λ/4 - without end correction L + c = 3λ/4 - with end correction Diagram: third harmonic/resonance

From: L = 5λ/4 - without end correction L + c = 5λ/4 - with end correction

Generally

Without end correction Ln = ((2n - 1 )λ)/4

Without end correction Ln + c = ((2n - 1)λ)/4

Where:

n = n^th harmonic

I_n = frequency of n^th harmonic

Example,

A turning fork of frequency 512 Hz is sounded at the mouth of a tube closed at one end with a movable piston. It is found that resonance occurs when the column of air is 18cm long and again when the column is 51cm long. Find wave length and velocity of sound in air.

Data given

Frequency, f = 512Hz

First column length, Li = 18cm = 0.18m.

Second column length, L2 = 51cm = 0.51m.

Wave length of sound in air, A = ?

Velocity of sound in air, v = ?

Solution

From: Li = 1λ/4 - - - - 1

L2 = 3λ/4- - - - 2

Solve simultaneous equation

Equation 2 minus equation 1

L2 — Li = 3λ/4 -1λ/4

L2 — Li = 2λ/4

L2 — Li =

0.51 - 0.18 = λ/2

0.33 = λ/2

= 0.33 x 2 = 0.66m

=0.66m

From: v = λf

v = 0.66 x 512 = 338 v = 338m/

Therefore the wave length of sound is 0.66m and velocity of sound in air is 338m/s

Example,

In a closed pipe, the first resonance is at 23cm and second at 73cm. determines the wave length of the sound and the end correction of pipe.

Data given

First length, Li = 23cm = 0.23m

Second length, L2 = 73cm = 0.73m

Wave length of sound, λ = ?

End correction of pipe, c = ?

Solution

From: Li + c = 1λ/4 - - - - 1

L2 + c = 3λ/4- - - - 2

Solve simultaneous equation

Equation 2 minus equation 1

L2 + C - Li - C = 3λ/4 -1λ/4

L2- Li = 2λ/4

L2- L1= λ/2

0.73 - 0.23 = λ/2

0.50 = λ/2

λ = 0.5 x 2 = 1.00m

λ= lm

From: equation 1

L1+ c = 1 λ/4 - make c subject

c = (1λ/4)- Li

c = ((1 x 1)/4)- 0.23

c = 0.25 - 0.23

c = 0.02m

Therefore the end correction of pipe is 0.002m and wave length of sound 0.m

Example, NECTA 1997 QN: 09

(a) Identify three characteristics of sound which distinguish one note from another. Hence state the physical factors which correspondingly define the mention characteristics

(b)A resonance tube whose one end is closed and other open, resonance to a note of frequency 560Hz when the length of the air column is 15cm. determine the wave length of this sound in air. What is the shortest length of the air column which resonates in similar conditions to a note of frequency 1000Hz

Solution

(a) (i) frequency

(ii) Loudness (amplitude)

(iii) Quality of music note (Timbre)

(b) Data given

First Frequency, fi = 560Hz

First Column length, Li = 15cm = 0.15m First Wave length of sound in air, λl = ? Second Frequency, f2 = 1000Hz

Shortest length, 12 = ?

Solution

First: find Wave length of sound in air, λ = ?

From: L = 3λ/4

Al = 41/3 = (4 x 0.15)/3 = 0.12m

= 0.12m

Second: find Shortest length, 12 = ? Note: sound will travel in same speed

From: v = λ1f1 = 560 x 0.12 = 67.2m/s Then: A2 = V/f2 = 67.2/1000 = 0.0672m From: L2 = 3λ₂/4 = (3 x 0.0672)/4 = 0.0504

L2 = 0.0504m

Resonance in Opened Pipe

Consider the diagram below

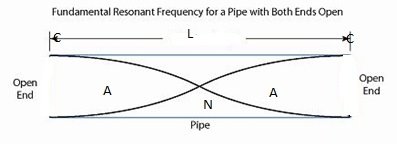
Where:

c = end correction

Since: opened twice end correction doubled

Then: L = λ/2

From: L = λ/2 - without end correction L + c = λ/2 - with end correction

Diagram: second harmonic/resonance

From: L = 2λ/2 - without end correction L + c = 2λ/2 - with end correction

Diagram: third harmonic/resonance

________________________

From: L = 3λ/2 - without end correction

L + c = 3λ/2 - with end correction

Generally

Without end correction Ln = nλ/2

Without end correction Ln + 2c = nλ/2

Where:

n = nth harmonic

I_n = frequency of nth harmonic

Example,

A turning fork of frequency 250Hz is used to produce resonance in an opened pipe. Given that the velocity of sound in air is 350m/s. find the length of tube which gives

a) First resonance

b) Third resonance

Data given

Sound frequency, f = 250Hz

Sound velocity, v = 350m/s

First resonance Length, Li = ?

Second resonance Length, L2 = ?

Solution

From: Ln = nλ/2

Find wave length first

From: v = λf -make λ subject

A = v/f = 350/250 = 1.4m

(a) First resonance Length, Li = ?

From: L1 = λ/2

L1 = λ/2 = 1.4/2 = 0.7m

L1 = 0.7m

(b)Second resonance Length, L2 = ? From: L2 = 2λ/2

L2 = 2λ/2 = (1.4 x 2)/2 = 2.8/2 = 1.4

L2 = 1.4m

Beats

Beats is the fall or rise in loudness of sound when two sources of sound of nearly equal frequencies produce sound together.

Formation of Beats

Beats formed when two/more sounds instruments (e.g. forks) of nearly equal pitch are played/sounded together. As a results a regular rise and fall in the loudness occurs as the waves generated by the instruments interfere constructively and destructively respectively.

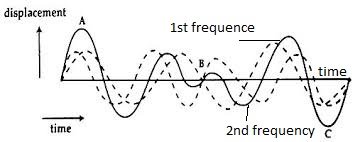
The Beat frequency/number is given by Bf=fi-f2orf2-fi

Example,

A 256Hz turning fork produces sound at the same time with a 249Hz turning fork. What is the beat frequency?

Data given

First frequency,fi = 256Hz

Second frequency,f2 = 249Hz

Beat frequency, Bf = ?

Solution

From: Bf = f2

Bf = fi- f2= 256 249 = 7Hz

Bf = 7Hz

Example, : NECTA 2010, QN: 10

(a) (I) Distinguish between longitudinal wave and transverse wave

(ii) Explain how beats are formed

(b)A light wave is refracted into an optically less median. What change will occur in.

(i) The frequency?

(ii) The speed?

(iii) The wavelength?

(c) (i) what is an echo

(ii) A sound is sent out from the ship and its reflection from the ocean floor returns one second later. Assuming that the velocity of sound in water is 1500m/s. how deep is the ocean?

Data given

Time taken by echo, t = ls

Wave velocity in air, v =

Distance moved by sound, 2d = ?

Solution

From: 2d = v x t

2d = 1500 x 1

2d = 1500m

d= 750m

Example, : NECTA 2011, QN: 06

(a) (i) What is a sonometer?

(ii) Briefly explain when resonance is said to occur.

(b)Two boys are stand 200m apart on one side of a high vertical cliff at the same perpendicular distance from it. When one fires a gun, the other hears the sound 0.6seconds after the flash and the second sound 0.25second after the first sound. Calculate the perpendicular distance of the boys from the cliff

(c) A diagram below illustrates part of the displacement-time graph of a wave travel with velocity of 2m/s.

First sound

Distance of sound to other boy, L = 200m

Time taken to other boy, ti = 0.65s Sound Speed, v = L/ti

v = 200/0.65 = 307.69m/s

v = 307.69m/s

Second sound

Echo time, t2 = 0.65 + 0.255 = 0.85s

Distance of echo, d = ?

From: 2d = v x t2

2d = 307.69 x 0.85 = 261.54

d = 130.77m

Now: perpendicular distance, D = ?

From: Pythagoras theorem

D² + 100² = d²

D² = d² - 100²= (130.77)²- 100²

D² = 17100.79 - 10000

D² = 7100.79 = (84.27)²

D = 84.27m

(c) Data given

Speed, v = 2m/s Amplitude, A = 0.2m

Period, T = 0.1s Frequency, f = ? Wave length, λ = ?

Solution

1. The amplitude is 0.2m
2. Frequency, f = ?
3. From: f = 1/T

f = 1/T = 1/0.1 = 10 f = 10Hz

2. Wave length, λ = ?

From: , λ = v/f

λ = v/f = 2/10 = 0.2

λ = 0.2m

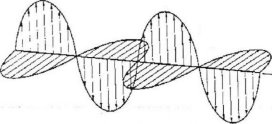
Electromagnetic Waves

Electromagnetic wave is the wave travel perpendicularly to both electric and magnetic field. Include

Diagram:

Electromagnetic wave include the follows

1. Radio wave
2. Microwaves
3. Infrared radiation

iv. Visible light

v. Ultraviolet rays

vi. X-rays

vii. Gamma rays

Nb:

• It produced when electrically charged particles oscillate or change energy
• The greater the energy change, the higher the frequency of the resulting wave
• In vacuum propagated in speed of light

Properties of Electromagnetic Waves

It is transverse waves which exhibit the following characteristics

 Do not require material medium for travel

 It undergoes reflection, refraction, interference and diffraction.

 Travel at speed of 3 x10⁸ m/s in vacuum.

 They carry no electric charge.

 Transfer energy in form of electric & magnetic field.

 They obey wave equation, v = λf

Electromagnetic Spectrum

Electromagnetic spectrum is a continuous band of all electromagnetic waves arranged in order of increasing or decrease frequencies or wavelength. It divided into seven regions or bands

Tables of Electromagnetic Spectrum

Wavelength (m)	Region	Frequency (H)
>10-1	Radio waves	>3 x 109
10-1- 10-4	Micro waves	3x109-3x1012
10-4-10-7	Infrared	3x1012- 4.3x1014
7x10-7-4x10 -7	Visible light	4.3x1014- 7.5x1014
4x10-7-10-9	Ultraviol et light	7.5x1014- 3x1017
10-9-10- 1	X-rays	3x1017- 3x1019
<10-11	Gamm a rays	>3x1019

Electromagnetic Spectrum Observation. There are two observations about electromagnetic spectrum include

• It continuous: means each band merges into next and there is no gap between their frequencies
• Some Wave length overlap: in some case there is overlap of wave length so we have to name according to source not the wave length, for Example, X-rays and Gamma rays

Radio Waves

It has the longest wavelength in the electromagnetic spectrum

Category of Radio Wave

It divided into the following

 Long waves (LW)

 Medium waves (MW)

 Short waves (SW), include Very high frequency (VHF) and ultra high frequency (VHF)

Sources of Radio Waves

It produced by;

• Alternating electric currents flowing through in special conductor called antennae
• Special circuits called oscillator.
• Object in space such as planets, comets, stars and galaxies

Detection of Radio Waves

Radio waves are detected using specially designed antennae such as those used in radios and televisions.

Uses of Radio Waves

• Broadcasting of information by radio and television channels is achieved using radio waves.
• Astronomers use large radio telescopes to collect and study radio waves from distant stars and galaxies.

Microwaves

Microwaves have a short wavelength of between 10^-4m to about 0.1 m

Sources of Microwaves

Microwaves are produced by oscillation of charges in special antennae mounted dishes. Micro waves are also produced in devices called magnetrons.

Detection of Microwaves

Micro wave can be detected by using special receiver which converts radio wave energy to sound called RADAR (Radio Detection and Ranging)

Uses of Microwaves

 Microwaves are used in cooking. In a microwave oven, microwave pass through the food and are absorbed by the food molecules.

 Radar system used microwave for detection of position, speed, and other characteristics of remote objects.

 Are used in long-distance
communication because they are not affected by clouds or other atmospheric condition.

Infrared Waves

Infrared radiation has frequency of between 10¹² and 10¹⁴ Hz. It has heating effect

Sources of Infrared Waves

It produced by vibration of atoms and molecules due to their thermal energy. All hot bodies emit infrared radiation

Detection of Infrared Waves

It detected by black bulb thermometer, photographic films, Thermistor and phototransistors.

Uses of Infrared Waves

 It is used to cook food in convectional ovens

 It is used in remote control, night vision device, fibre-optic telecommunication and security system

 Used in infrared lasers that produce infrared beams that can be used to read information on compact discs.

 Used in the chemical industry to determine molecular structure and composition of substances by studying their infrared emission or absorption.

 Used in the medical field to locate diseased tissues (these areas emit abnormal heat compared to the other areas) and injury by analysing the body tissue and body fluid.

 Used for military purposes where infrared imaging devices are used to locate enemy troops in the dark, detect hidden mines, arm caches, to guide anti-aircraft missiles, etc.

 Infrared radiation is used to de-ice the wings of aircraft

 In industries they are used for welding plastics, drying prints, curing (process of hardening) coatings etc.

 Used in locating missing people and people trapped under collapsed buildings (Infrared imaging devices are used)

 Used to locate overheating in electric system

Visible Light

Visible light is the range of electromagnetic wave frequencies to which human eyes are sensitive.

Sources Of Visible Light

It produced by electrons transitions within an atom (anything thats hot enough to glow). The sun emits 50% of visible light

Detection of Visible Light

It detected by eyes, photographic films and photocells

Uses of Visible Light

Visible light has very many uses

• Photography
• Vision
• Photosynthesis

Ultraviolet Light

It has short wavelength than visible light

Sources of Ultraviolet Light

• It produced by electrons transitions within an atom but more energetically
• Sun emit ultraviolet radiation which absorbed by ozone layer
• Electric arc used for welding emit ultraviolet radiation

Detection of Ultraviolet Light

It can detect by

• Photographic film (ultraviolet light does not allowed to pass through across ordinary glass until fitted with quartz materials)
• Fluorescent materials which absorb and re-emit ultraviolet light

Uses of Ultraviolet Light

 It stimulates of production of vitamin D in human skin

 It used in treatment of skin conditions such as psoriasis

 lt is used as germicidal agent. Sterilization of food and purification of air and water.

 lt used to detect forget document and fake currencies. E.g. bank.

 lt is used extensively in astronomical observation

NB:

Ultraviolet light can cause damage of skin, eyes, immune system (mutation) when prolonged exposure.

X-Rays

X-rays Is the electromagnetic wave with short wavelength and very high frequency produced b when fast-moving electrons hit a metal target. It also called ionization radiation because if encounter an atom cause loss of electrons

Sources of X-Rays

It produced when electron accelerated in very high velocity hit a metal target x-rays Tube.

Detection of X-Rays

It can detect by the following methods

 By using photographic plate

 By using x-ray film in a cassette

 By using rare earth element screens

Properties of X-Rays

• travel in straight line at the velocity of light
• they cannot be deflected by electric or magnetic field
• they can produce fluorescence.
• they affect photographic film.
• they penetrate matter but depend on density of matter.
• they ionize gases.
• can be diffracted by crystals

Uses of X-Rays

 x-ray photography for diagnosis of denser tissue like bones

 it use in treatment of cancer.

 used in industry to detect flaws in metal casting and welded joint such as in the aeroplane structure or building structure.

 they used in airports and seaport for non-invasive security search.

 they are used in the study of the arrangement of atoms in solid.

 used to produce images of very small object

Gamma Rays

Gamma ray is more energetically among electromagnetic wave. Also can cause ionization.

Sources of Gamma Rays

• It produced in space such as solar flares, supernovae, neutron star, black holes and active galaxies. All gamma ray from space absorbed by earths atmosphere.
• It produced by radioactive decay of atoms (natural radioactivity)
• lt produced by nuclear fission (in atomic bombs and nuclear reactors)

Detection of Gamma Rays

It can detect by the following methods

• Photographic films
• Geiger-Muller tube
• Cloud chamber

Uses of Gamma Rays

• X-ray photography for diagnosis of denser tissue like bones
• It use in treatment of cancer
• lt used in agriculture to obtain new plant varieties which are disease-resistance and give more yield

Example, NECTA 1995: QN 07

(a) Explain why radio waves are similar to light waves but not sound waves

(b)A radio station transmits a signal of wave 1500m. Calculate the frequency of this signal

Data given

Wave length, A = 1500m

Wave Velocity, v = 3 x10⁸ m/s

But: Frequency, f = ?

From: V = of

Then: f = V/A

f = 3 x10⁸ /1500 = 200000 Hz = 200 KHz f = 200 KHz

Example, NECTA 1998: QN 04

What is diffraction of wave?

Illustrate how plane water wave fronts are diffracted on passing through a narrow gap

(i) Is it possible for light to be diffracted on passing through an open window? (ii) Give an explanation on your answer above

Example, NECTA 1998: QN 08

What is the fundamental frequency of a vibrating string?

Sonometer consists of a taut steel wire fixed between two bridges 100cm apart. Defining the first harmonic, second harmonic, third harmonic and fouth harmonic. Explain ow overtones can be obtained.

WAVES

1. A string of length 1.2 m is stretched and the made to vibrate so that a stationary wave consting of two loops is produced.

a) Draw a sketch of the wave

b) Determine the length of the wavelength of the wave

2. A wire of length 20cm and mass 1.2g is under a tension of the 120N. determine the wave length of the wave.

a) The fundamental frequency of vibration.

b) The frequency of the third harmonic

3. The fundamental frequency of vibration of a string is F. what will be the fundamental frequency of the string be if length is of the of the sting is halved and the tension is increased four times?
4. A closed pipe (open at one end) has a fundamental frequency of 400Hz. Calculate:

a) The frequency of the first overtone

b) The fundamental frequency of an open pipe of the same length

5. A speaker emitting a note of frequency 250 Hz is placed over the upper end of a vertical tube filled with water. When the water is gradually run down the tube air column resonates initially when the water is gradually run down the tube air column resonates initially when the water level is 9.98 cm below the top of the tube. Determine :

a) The speed of sound in air

b) The end correction

SAMPLENECTA QUESTIONS.

• (a) Define

(i) Amplitude

(ii) Periodic time.

• (b) In a closed pipe, the first resonance is at 23cm and second at 73cm. Determine the wavelength of sound and the End correction.

• Answer; Wavelength , End correction,

• (a) What is meant by the following terms?

(i) Resonance (ii) Overtones

• (b) Briefly explain the following:

(i) The fundamental frequency may alter during the day

(ii) Notes of the same pitch played on violin and a flute sound different.

• (c) The frequency obtained from a plucked string is 400Hz when the tension is 2N. Calculate;

(i) The frequency when tension is 8N

Answer;

(ii) The tension needed to produce a note of

frequency 600Hz.

Answer;

• (a) (i) In longitudinal waves, the particles vibrate to and fro forming region of compressions and rarefactions. Explain the terms compressions and rarefactions. [02]

(ii) State the principle of superposition. [01]

• (b) (i) State two differences between Mechanical waves and Electromagnetic waves. [02] (ii) Calculate the wavelength of green light of frequency

• (c) A stretched string has a fundamental frequency of 600Hz. Determine the new frequency if the tension is doubled and its length is halved. [03]

• (a) (i) What happens when water waves travel from a deep part to a shallow part?

(ii)Define the term interference as used in waves.

• (b) State two conditions for constructive interference to occur.

• (c) A man stands on flat ground some distance from a tall vertical cliff and fires a gun. The report comes 1.9 seconds later. He then walks 200 meters further from the cliff and fires again. The report comes 3.1 seconds later. Calculate the speed of sound and find how far he was originally from the cliff.

• (a) Explain the basic differences between

(i) Mechanical waves and electromagnetic waves. (ii) Longitudinal waves and transverse waves.

• (b) Name two examples of waves that fall into each of the following categories;

(i) Transverse waves. (ii) Mechanical waves.

(iii) Electromagnetic waves

(iv) Longitudinal waves.

© The standing waves that form in some cavity include the fundamental, some overtones and some harmonics. Give the relationship between;

(i) Fundamental frequency and the harmonic frequency.

(ii) The fundamental frequency and the overtone frequency.