APPLICATION OF VECTOR

At the end of this Topic you should be able to:
a) Distinguish between scalar and vector quantities
b) Add vectors using graphical methods
c) State the triangular and parallelogram law of forces

d)Explain the concept of relative motion
e) Calculate relative motion of bodies
f) Apply the concept of relative motion in daily life

KEY TERMS AND CONCEPTS.

• Scalar quantity- this is quantity that that has only magnitude
• Vector quantity – is a quantity with both magnitude and direction
• Resultant vector- this is the vector obtained when two vectors are connected by a third line.
• Triangle law of addition- It states that; "If three forces are in equilibrium and that two of the forces are represented in magnitude and direction by two sides of a triangle, then the third side of the triangle represents the resultant of the two forces"
• Parallelogram law of addition states; "If two forces/vectors are represented by the two sides given and they include angle
  between them, then resultant of the two forces/vectors will be represented by the diagonal from their common point of a parallelogram formed by the two forces/vectors"
• Relative velocity- This is the velocity of a body in relation to another

Scalar quantity.

Is a physical quantity with both magnitude only.

Examples are time, speed,distance,temperature, energy,mass, area, volume, density, volume, electric current etc.

Vector Quantities

Vector quantity is the any physical quantity that has both magnitude and direction.

Example, force, displacement, velocity, momentum, acceleration, etc

Vector Arithmetic

Scalar quantity can be added, multiplied, divided or subtracted.

Example, if you have two liquid in different measuring cylinder let say fist one contain 10 cm³ and second contain 20cm³ if you asked to find total volume you must add to obtain total volume

Vector quantity can be represented on a diagram by a directed line segment, consider the diagram below.

a

The length of line segment represents the magnitude and the arrow represents the direction

NB:

• The direction can be represented by using compass direction
• Two vector are equal if the magnitude and direction the same.

When adding two or more vectors, by mathematical formula is used to sum up vectors. For example, pythogoras theorem, and trigonometric ratios.

• The triangle method and parallelogram method are used to adding two vectors.
• The vector we get after the adding of two or more vectors is called resultant vector
• Resultant vector can be added by mathematical or graphical/drawing
• Resultant vector is measured as an anticlockwise angle of rotation from due east

Adding By graphical Method

The following are steps followed when adding two or more vectors by graphical method

 Choose a suitable scale and write it down on a graph paper

 Pick starting and draw the first vector to scale direction stated (indicate the magnitude and direction)

 Starting from the head of the first vector, draw the second vector to scale in the started direction until all given vectors finished

 Draw the line to connect tail of the first drawn vector and the head of the last vector. This is called resultant vector

 Measure the length of the resultant vector and convert to actual unit

 Determine the direction of vector

Example,

Suppose a man walks starting from point A, a distance of 20m due north and then walks 15m due east. Find his new position from A

Solution

• Using a scale of 1 cm to represent 5 m
• Draw a vector AB 4cm due north.
• From B draw BD 3cm due east.
• Join A and D point

The resultant diagram is a triangle as shown below

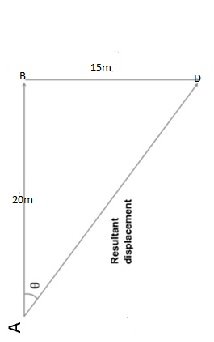
5. Measure the length of AD

AD = 5 cm

Change to actual unit

lcm = 5 m

5 cm = ?

Cross multiplication you get 25 m

6. Determine the direction of vector

Tanθ = = 0.75

θ= 36⁰51

Therefore position of D is represented by vector AD of magnitude 25 m at an angle of 36⁰51 east of north

The Triangle Method/Triangle Law

The triangle law is appropriate when adding two vector quantities. The law state that

"If three forces are in equilibrium and that two of the forces are represented in
magnitude and direction by two sides of a triangle, then the third side of the triangle represents the resultant of the two forces"

Example,

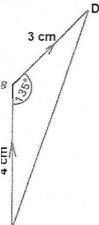
A brick is pulled by a force of 4N acting northward and another force of 3N acting north-east. Find the resultant of these two forces.

Solution

Data

Initial force, F₁=4N northward

Final force, F₂=3N north-east

Steps

i/ Using a scale of lcm to represent 1 N

ii/ Draw a vector AB 4cm due north.

iii/ From B draw BD 3cm at 45⁰

iv/Join A and D point

The resultant diagram is a triangle as shown below

v/ Measure the length of AD

AD = 6.5 cm

Change to actual unit

lcm = 1 N

6.5 cm = ?

Cross multiplication you get 6.5 N

Therefore the resultant of these two forces= 6.5 N

Example,

Two forces, one 8 N and the other 6 N, are acting on a body. Given that the two
forces are acting perpendicularly to eachother, find the magnitude of the third force which would just counter the two forces.

Solution

Data

Force, F₁=8N

Force, F₂=6N

Stapes

i/ Using a scale of 1 cm to represent 2 N

ii/ Draw a vector AB 4cm due north.

iii/ From B draw BC 3cm at 90⁰

iv/Join A and C point

The resultant diagram is a triangle as shown below

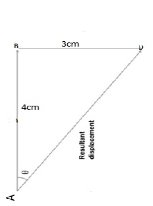
v/ Measure the length of AC

AD = 5 cm

Change to actual unit

lcm = 2 N

5 cm = ?

Cross multiplication you get 10 N

Therefore magnitude of third force is 10 N

Parallelogram Method

The parallelogram law of vector is applicable when adding two vector quantities. The law state that

"If two forces/vectors are represented by the two sides given and they include angle
between them, then resultant of the two forces/vectors will be represented by the diagonal from their common point of a parallelogram formed by the two forces/vectors"

Example1;

Two forces AB and AD of magnitude 40 N and 60 N respective are pulling a body on horizontal table. If the two forces makes an angle 30⁰ between them, find the resultant force on the, body.

Solution

Data

Force AB, F_AB=40N

Force AD, F_AD=60N

Angle between, θ=30⁰

i/ Using a scale of 1 cm to represent 10 N

ii/ Draw a vector AD 6 cm horizontal from point A

iii/ From point A draw AB 3 cm at 30⁰ from vector AD

iii/Complete the parallelogram ABCD

iv/ Join A and c point

The resultant diagram is a triangle as shown below

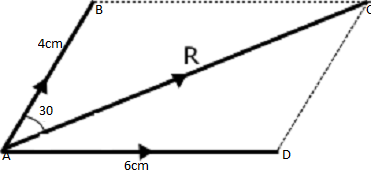
v/Measure the length of Ac

Ac = 9.7 cm

Change to actual unit

1 cm = 10 N

9.7 cm = ?

Cross multiplication you get 97 N

Therefore the resultant of these two forces 6.5 N

Example 2;

Two ropes of 3 m and 6 m long are tied to a ceiling and their free ends are pulled by a force of 100 N as shown in the figure below. Find the tensions in each rope if they make angle 30° between them.

Diagram:

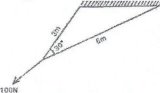
Data

Legth, l₁=3m

Length, l₂=6m

Force, F=100N

Angle between, θ=30⁰

Solution

Steps

i/ Using a scale of 1 cm to represent 1 m

iii/ Draw a vector AD 6 cm horizontal from point A

iii/ From point A draw AB 3 cm at 30⁰ from vector AD

iv/Complete the parallelogram ABCD

v/ Join A and c point

The resultant diagram is a triangle as
shown below

A 6 cm

vi/Measure the length of Ac

AC = 8.7 cm

AC is the equal to 100 N because action is equal to opposite reaction,

AC = 8.7cm =100 N

Now:

Tension at 3 cm calculated by:

8.7 cm = 100 N

3 cm = ?

Cross multiplication you get 34.5 N

Therefore the Tension at 3 cm is 34.50N

Then:

Tension at 6 cm calculated by:

8.7 cm = 100 N

6 cm = ?

Cross multiplication you get 69 N

Therefore the Tension at 6 cm is 69 N

Example,

Find the resultant force when two forces act as shown in the figure below.

6N

8N

Solution

Joining to line to get resultant force

8N D

i/ Using a scale of 1 cm to represent 1 N

ii/ Draw a vector AD 8 cm horizontal from point A

iii/ From point A draw AB 6 cm at 90⁰ from vector AD

iv/Complete the parallelogram ABCD V/ Measure the length of Ac

Ac = 10 cm

Change to actual unit

1cm = 1N

10cm = ?

Cross multiplication you get 10N

Therefore the resultant of these two forces 10N

Example,

Find the resultant force, F, when two forces,

9N and 15N, act on an object with an angle of 60⁰ between them.

Solution

i/Using a scale of 1cm to represent 3N

ii/Draw a vector AD 5cm horizontal from point A

iii/ From point A draw AB 3cm at 60⁰ from vector AD

iv/Complete the parallelogram ABCD

v/ Join A and c point

The resultant diagram is a triangle as
shown below

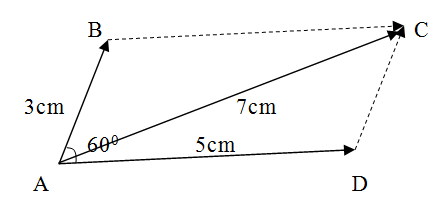
v/Measure the length of AC

AC = 7 cm

Change to actual unit

lcm = 3 N 7 cm = ?

Cross multiplication you get 21 N

Therefore the resultant force, F is 21 N

Relative Velocity

Relative velocity is the velocity of a body which observed by another moving or stationary body.

Or

Relative velocity is the velocity of a body with relative to the moving observer.

Nb:

• Velocity of one object let say V_A respect another object let say V_B is denoted by symbol V_AB.
• if all object moving to the same direction, it seems to observe low speed, therefore we minus two velocity of moving body, (^_V_B)

V_AB = V_A + (^_V_B)

V_AB = V_A – V_B

• if all object moving to the opposite direction, it seems to observe high speed, therefore we plus two velocity of moving body, (+V_B)

V_AB = V_A + (+V_B)

V_AB = V_A + V_B

Relative velocity also can be calculated by triangle method and by parallelogram methods.

Example,

A plane travelling at a velocity of 100 km/h to the South encounters a side wind blowing at 25 km/h to the West. What is its velocity relative to an observer on the ground?

Data

Velocity of plane, V_p= 100km/h south

Velocity of plane, V_w= 25km/h west

Solution:

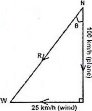
By using Pythagoras theorem,

R²= 25² + 100²

R² = 625 + 10000

R²= 10625

R=

R = 103.1 km/h

Direction of resultant

Cos θ =

Cos θ =

Cos θ = 0.9699

θ= 14⁰ - clockwise to the east with the southward direction.

Since: Resultant vector is measured as an anticlockwise angle of rotation from due east

θ = 270° - 140- anticlockwise to the east θ = 256°

Example,

Car A is moving with a velocity of 20 m/s while car B is moving with a velocity of 30 m/s.

Calculate the velocity of car B relative to car A if:

{a} they are moving in the same direction

{b} They are moving in the opposite directions.

Data given

Velocity of Car A, V_A = 20 m/s

Velocity of Car B, V_B = 30 m/s

Relative velocity, V_BA = ?

Solution:

{a} they are moving in the same direction

From: V_BA = V_B -V_A

V_BA =30 - 20

V_BA = 10 m/s

{b} They are moving in the opposite directions.

From: V_BA = V_B + V_A

V_BA = 30 + 20

V_BA = 50 m/s

Resolution of the Vector

As we study at trigonometrically ratio when we have values of hypotenuse and angle formed with horizontal we can calculate vertical component and horizontal component.

Consider the diagram below where the toy car pulls at a certain angle but it seems to move horizontally due to horizontal force/vector, not only that but vertical force/vector are formed

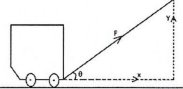
From the diagram:

Horizontal force/vector = x

Vertical force/vector = y

Extract the triangle from the above diagram

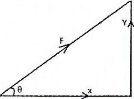
Horizontal force/vector is given by the formula

From:

cos θ = multiply by F both sides you get

x = Fcos θ

Vertical force/vector is given by the formula

From:

Sin θ = multiply for F both sides you get

y= Fsin 8

Example,

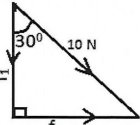
A nail is being pulled using a string from a wall. The string forms an angle of 30° with the normal. If the force being used is 10 N, part of the force will tend to bend the nail while the other part will try to pull it out.

Figure:

{a} Tend to bend the nails?

{b} Tend to pull the nails out?

Data

Force applied, F=10N

Angle made, θ=30⁰

Solution:

Change the information above into vector form

F2

{a} Force tends to bend the nails, F₁ = ?

F₁ = 10 x cos 30⁰

= 10 x 0.866

F₁ = 8.66 N

{b} Force tends to pull the nails out, F₂= ?

F₂ = 10 x sin 30⁰

F₂= 10x0.5

F₂ = 5.0 N

Example,

A body is being acted on by two forces: F₁ = 18N acting at an angle of 25° and F₂ = 30 N acting at 140° from due East. Find the resultant of the two forces, F, by separating the forces into x- and y-components.

Solution:

Draw the diagram first

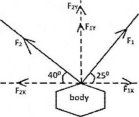
First find F_1x and F_2x

Where: F₁= 18N F₂ = 30 N From: X = F. Cos 0

F_1x = F₁ Cos 25

F_1x = 18 x Cos 25

F_1x = 18 x 0.9063

F_1x = 16.31N - toward east

F_2x = 22.98 N - toward west θ=76.06° - to the west or θ=103.94°- to the east

Assume the wanted direction is east so the an direction of force to west will be negative.

Find their net force, F_x = ?

F_x = F_1x + F_2X

F_x = 16.31 + (-22.98)

F_x = 16.31 - 22.98

F_x = - 6.67N - toward west

Second find F_ly and F_2y

Where:

F₁= 1=18 N F₂ = 30 N

From: y= F. Sinθ

F_ly .= F₁. Sin 25

F_ly = 18 x Sin 25

F_ly = 18 x 0.4226

F_ly = 7.6N - toward north

Then:

F_2y = F₁. Sin 40

F_2y = 30 x Sin 40

F_2y = 30 x 0.6428

F_2y = 19.28 N - toward north

Assume the wanted direction is north.

Find their net force, F_y = ?

F_y = F_ly +F_2y

F_y = 7.6 + 19.28

F_y=26.88N toward north

Modify the vector diagram

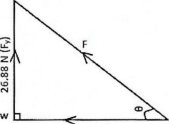
6.67 N (F_x)

Lastly find the resultant of the two forces, F =2

By using Pythagoras theorem,

R²= 26.88² + (-6.67²)

R = 27.70 N

Get the direction tanθ = F_y/F_x

tanθ=26.88/6.67

tan θ = 4.03

θ= 76.06⁰- to te west or θ= 103.94 to east

Therefore the resultant force is 27.70N at an angle of 103.94 to west.

SUMMARY

1. Quantities can be represented as a vector or scalars. Vectors have both magnitude and direction while scalars have magnitude only.
2. A vector quantity is represented quantity is represented graphically using a vector diagram. In a vector diagram, an arrow drawn to scale in a specific direction is to represent the vector.
3. A resultant vector that is net effect of two or more vectors.
4. The triangle law of vector addition states that if two vectors addition states that if two vectors are vectors are represented by two sides of a triangle in sequence, that if two sides of a triangle in sequence, then the third closing side of the triangle drawn from the tail of the first vector to the head of the two vector, represents the resultant of the two vectors in both magnitude and direction.
5. The parallelogram law of vector addition states that: if two vectors are represented by two adjacent sides of a parallelogram, then the diagonal of the parallelogram through the common point represents the sum of the two vectors in both magnitude and direction.
6. A two dimensional vector can be separated into two perpendicular vectors which are its components.
7. Relative velocity of a body with respect to another moving body.
8. We use the Pythagoras theorem , c² ═ a² ┼ b², to find the result vector of two perpendicular vectors of two perpendicular vectors.
9. A vector F has a component F cos o in a direction at angle o to itself and a component F Sin o in the perpendicular direct direction.

SAMPLE NECTA QUESTIONS

(a) State the parallelogram law of forces.

(b)(i) Distinguish between absolute velocity and relative velocity.

(ii) Wind is blowing 30° west of north at 20 km/hour. A bird is flying in the wind and its velocity relative to the ground is 90 km/hour at 75° west of north. Calculate the velocity and direction of the bird.

(c) (i) Define the coefficient of dynamic friction.

(ii) A body of mass 40 kg is placed in a straight track sloping at an angle of 45° to the horizontal. If the body is held from slipping by friction, calculate the normal reaction and the force of friction.

(a) State the parallelogram law of forces.

(b) (i) Distinguish between, Absolute velocity and relative velocity.

(ii) Wind is blowing west of north at 20km/hour. A bird is flying in the wind and its velocity relative to the ground is 90km/h at west of north. Calculate the velocity and direction of the bird.

(c) (i) Define, coefficient of dynamic friction.

(ii) A body of mass 40kg is placed in a straight track sloping at an angle to the horizontal . If the body is held from slipping by friction, calculate the normal reaction and the force of friction.