CHAPTER 01 : RELATIONS

By End Of This Topic You should be able to:

• To find relations between two sets and find relations between members in a set.
• To define domain and range and calculate domain and range
• To explain the inverse of a relation and show the inverse of a relation pictorially
• To find the inverse of a relation and draw a graph of the inverse of a relation
• To draw a graph of a relation represented by a linear inequality.

Relations

A relation "R" is the rule that connects or links the elements of one set with the elements of the other set.

Some examples of relations are listed below.

1. "Is a brother of "
2. "Is a sister of "
3. "Is a husband of "
4. "Is equal to "
5. "Is greater than "
6. "Is less than "

Normally relations between two sets are indicated by an arrow coming from one element of the first set going to the element of the other set.

Relations Between Two Sets

Find relations between two sets

The relation can be denoted as:

R = {(a, b): a is an element of the first set, b is an element of the second set}

Consider the following table

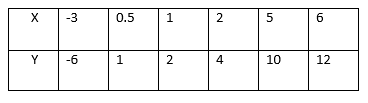
This is the relation which can be written as a set of ordered pairs {(-3, -6), (0.5, 1), (1, 2), (2, 4), (5, 10), (6, 12)}. The table shows that the relation satisfies the equation y=2x. The relation R defining the set of all ordered pairs (x, y) such that y = 2x can be written symbolically as:

R = {(x, y): y = 2X}.

Relations Between Members in a Set

Find relations between members in a set

Which of the following ordered pairs belong to the relation {(x, y): y>x}?

(1, 2), (2, 1), (-3, 4), (-3, -5), (2, 2), (-8, 0), (-8, -3).

Solution.

(1, 2), (-3, 4), (-8, 0), (8,-3).

Relations Pictorially

Demonstrate relations pictorially

For example the relation " is greater than " involving numbers 1,2,3,4,5 and 6 where 1,3 and 5 belong to set A and 2,4 and 6 belong to set B can be indicate as follows:-

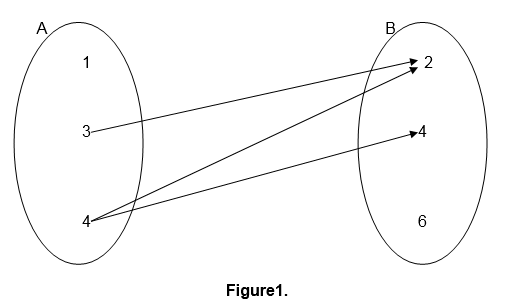
This kind of relation representation is referred to as pictorial representation.

Relations can also be defined in terms of ordered pairs (a,b) for which a is related to b and a is an element of set A while b is an element of set B.

For example the relation " is a factor of " for numbers 2,3,5,6,7 and 10 where 2,3,5 and 6 belong to set A and 6,7 and 10 belong to set B can be illustrated as follows:-

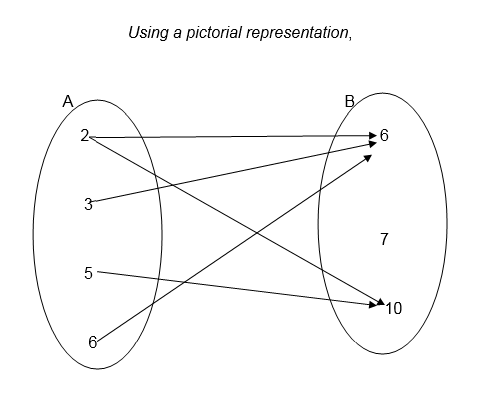
Example 1

1. Draw an arrow diagram to illustrate the relation which connects each element of set A with its square.

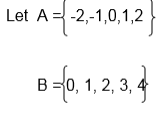
Solution

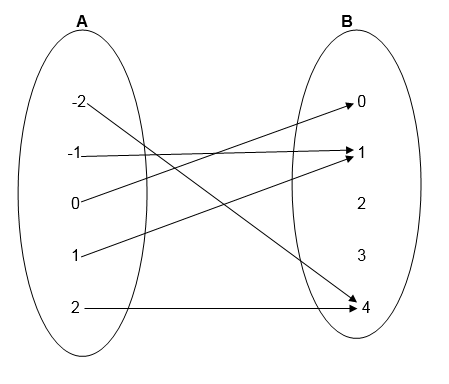
Example 2

Using the information given in example 1, write down the relation in set notation of ordered pairs. List the elements of ordered pairs.

Example 3

Consider the relation below:

Solution;

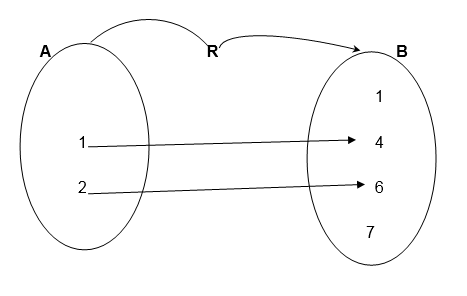
Example 4

Let X= {2, 3, 4 } and Y= {3 ,4, 5}

Draw an arrow diagram to illustrate the relation " is less than"

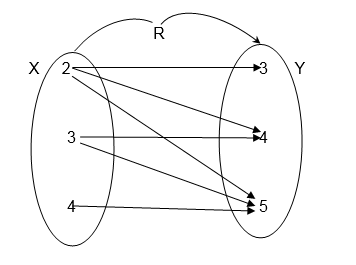
Exercise 1

Let P= {Tanzania, China, Burundi, Nigeria}

Draw a pictorial diagram between P and itself to show the relation

"Has a larger population than"

2. Let A = 9,10,14,12 and B = 2,5,7,9 Draw an arrow diagram between A and B to illustrate the relation " is a multiple of"

3.Let A = mass, Length, time and

B = {Centimeters, Seconds, Hours, Kilograms, Tones}

Use the set notation of ordered pairs to illustrate the relation "Can be measured in"

4. A group people contain the following; Paul Koko, Alice Juma, Paul Hassan and Musa Koko. Let F be the set of all first names, and S the set of all second names.

Draw an arrow diagram to show the connection between F and S

5. Let R={ (x, y): y=x+2}

Where x∈A and A ={ -1,0,1,2}

and y∈B, List all members of set B

Exercise 2

1. Let the relation be defined

3. Consider the following pictorial diagram representing a relation R.

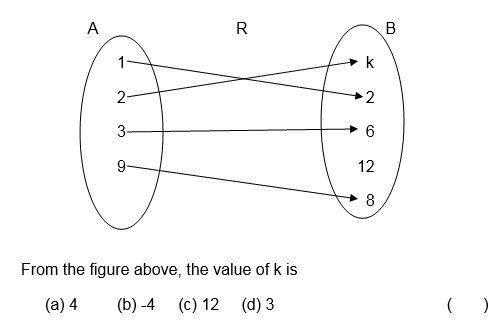
4. Let the relation R be defined as

5. A relation R on sets a and B where A = 1,2,3,4,5 and B = 7,8,9,10,11,12 is defined as " is a factor of "

A Graph of a Relation Represented by a Linear Inequality

Draw a graph of a relation represented by a linear inequality

Given a relation between two sets of numbers, a graph of the relation is obtained by plotting all the ordered pairs of numbers which occur in the relation

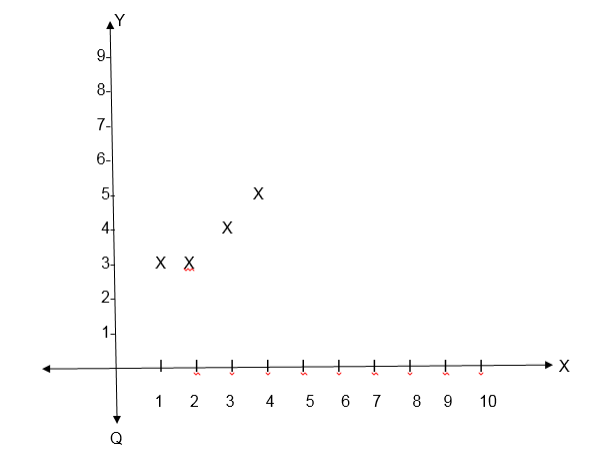
Consider the following relation

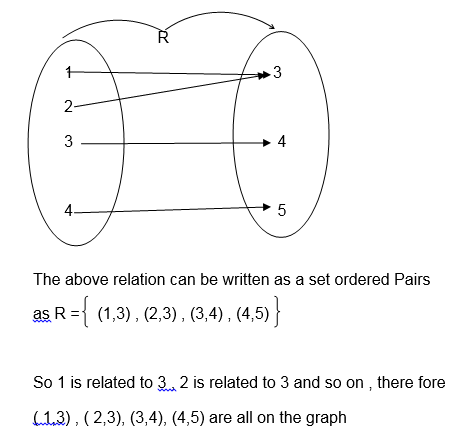
The graph of R is shown the following diagram( x-y plane).

Example 5

Solved:

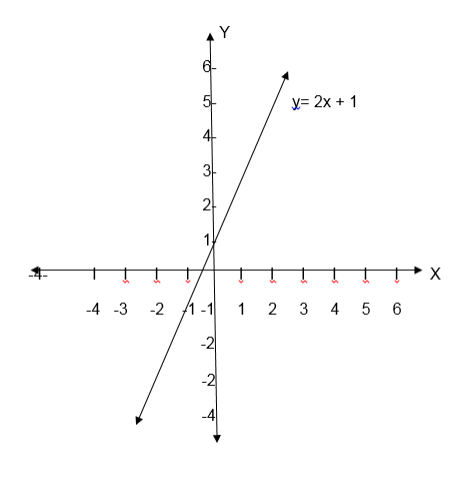
Note that some relations have graphs representing special figures like straight lines or curves.

Example 6

Draw the graph for the relation R= {(x, y): y = 2x +1} Where both x and y are real numbers.

Solution

The equation y = 2x +1 represents a straight line, this line passes throng uncountable points. To draw its graph we must have at least two points through which the line passes.

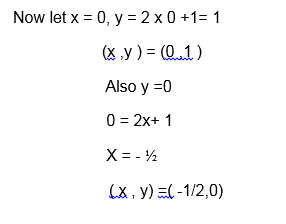
Graph;

Example 7

Let A = {-2,-1,0, 1, 2 } and B ={0,1,2,3,4}

Let the relation R be y= x^2, where x ∈A and y∈B. Draw the graph of R

Solution

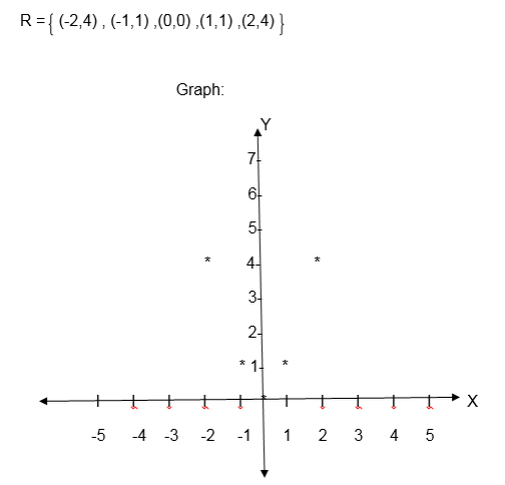
NB: When the relation is given by an equation such as y = f (x), the domain is the set containing x- values satisfying the equation and the range is the set of y-values satisfying the given equation.

Exercise 3

Test Yourself:

Quiz.

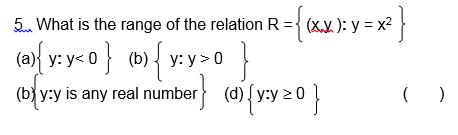
Domain and Range of a Relation

The Domain of Relation

State the domain of relation

Domain: The domain of a function is the set of all possible input values (often the "x" variable), which produce a valid output from a particular function. It is the set of all real numbers for which a function is mathematically defined.

The Range of a Relation

State the range of a relation

Range: The range is the set of all possible output values (usually the variable y, or sometimes expressed as f(x)), which result from using a particular function.

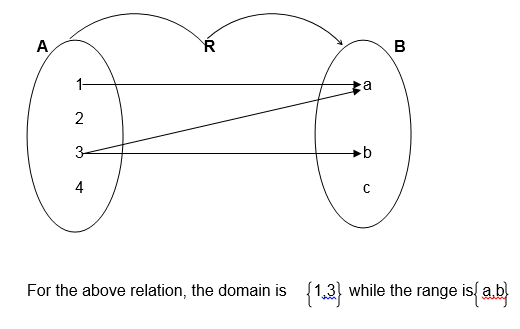
If R is the relation on two sets A and B such that set A is an independent set while B is the dependent set, then set A is the Domain while B is the Co-domain or Range.

Note that each member of set A must be mapped to at least one element of set B and each member of set B must be an image of at least one element in set A.

Consider the following relation

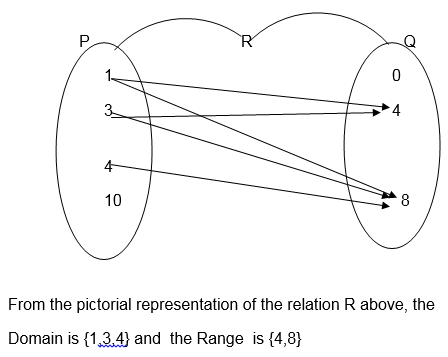
Example 8

Let P = 1,3,4,10 and Q = 0,4,8

Find the domain and range of the relation R:” is less than”

Example 9

Consider the relation below:

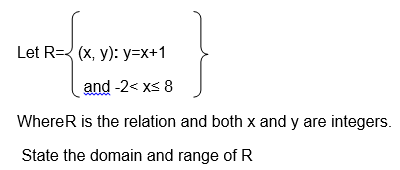
Exercise 4

1. Let A = { 3,5,7,9 } and B = {1,4,6,8 } , find the domain and range of the relation “is greater than on sets A and B

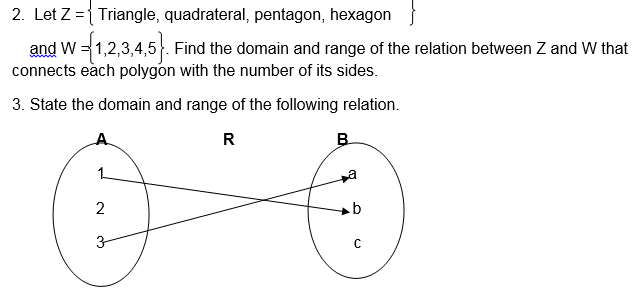
4. Let X ={3, 4, 5, 6} and

Y ={2, 4, 6, 8}

Draw the pictorial diagram to illustrate the relation “is less than or equal to‘ and state its domain and range

Inequalities:

The equations involving the signs < , ≤, > or ³ are called inequalities

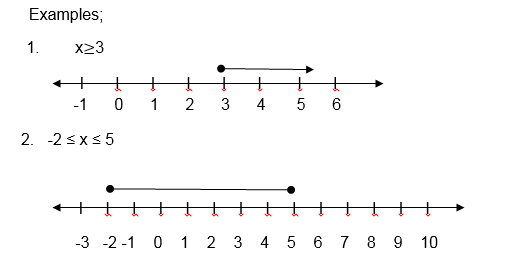
Eg. x<3 x is less than 3

x>3 x is greater than 3

x≤ 2 x is less or equal to 2

x³ 2 x is greater or equal to 2

x > y x is greater or than y etc

Inequalities can be shown on a number line as in the following

Inequalities involving two variables:

If the inequality involves two variables it is treated as an equation and its graph is drawn in such a way that a dotted line is used for > and < signs while normal lines are used for those involving ≤ and ≥.

The line drawn separates the x-y plane into two parts/regions

The region satisfying the given inequality is shaded and before shading it must be tested by choosing one point lying in any of the two regions,

Example 10

1. Draw the graph of the relation R = {(x, y): x>y}

Solution:

x>y is the line x =y but a dotted line is used.

Graph

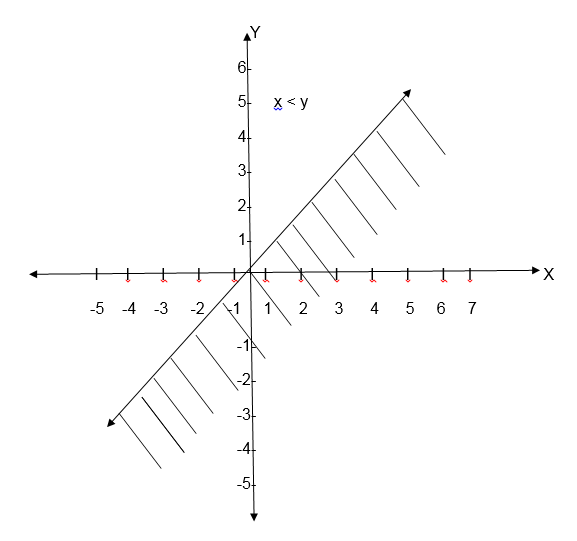
If you draw a graph of the relation R = {(x,y ) : x < y} , the same line is draw but shading is done on the upper part of the line.

Exercise 5

1. Draw the graph of the relation R = {(x,y ): x + y > 0}

2 .Draw the graph of the relation R = {( x ,y ) : x – y ³ -2}

3. Write down the inequality for the relation given by the following graph

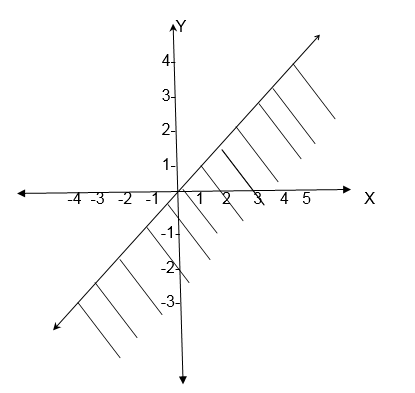
4. Draw a graph of the inequality for the relation x >-2 and shade the required region.

Domain and Range from the graph

Definition: Domain is the set of all x values that satisfy the given equation or inequality.

Similarly Range is the set of all y value satisfying the given equation or inequality

Example 11

1. Consider the following graph and state its domain and range.

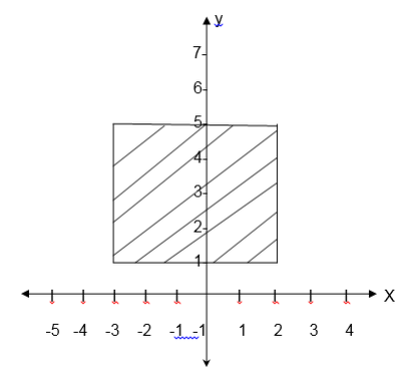
Solution

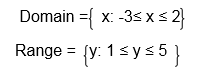
Example 12

State the domain and range of the relation whose graph is given below.

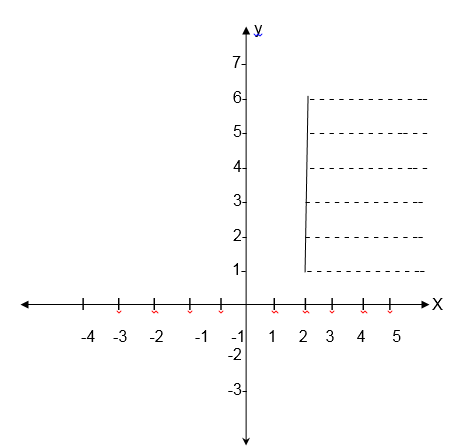
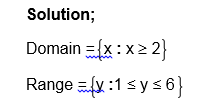
Inverse of a Relation

The Inverse of a Relation Pictorially

Explain the Inverse of a relation pictorially

If there is a relation between two sets A and B interchanging A and B gives the inverse of the relation.

If R is the relation, then its inverse is denoted by R^-1

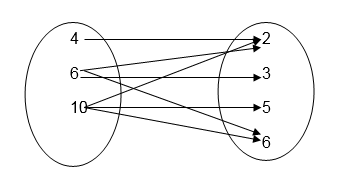
• If the relation is shown by an arrow diagram then reversing the direction of the arrow gives its inverse
• If the relation is given by ordered pair ( x, y) , then inter changing the variables gives inverse of the relation, that is (y,x) is the inverse of the relation. So domain of R = Range of R -1 and range of R = domain of R^-1

Example 13

1.

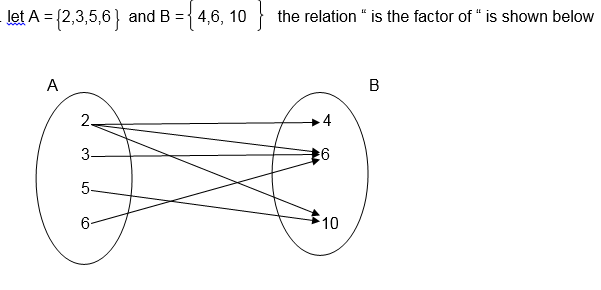
The inverse of this relation is “ is a multiple of “

Inverse of a Relation

Find inverse of a relation

Example 14

Find the inverse of the relation R ={ ( x, y): x+ 3≥ y}

Solution

R^-1 is obtained by inter changing the variables x and y.

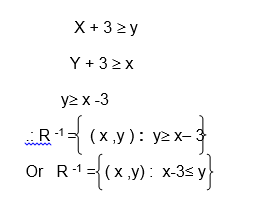
Example 15

Find the inverse of the relation

R ={ ( x , y ): y = 2x }

Solution

R ={( x , y ): y = 2x }

After interchanging the variable x and y, the equation

y = 2x becomes, x = 2y

or y = ½ x

so R^-1 = ( x, y ) : y = ½ x

Exercise 6

1 . Let A = 3,4,5 and B ‘= 1,4,7 find the inverse of the reaction “ is less than “ which maps an element from set A on to the element in set B

2 . Find the inverse of the relation R = {( x ,y ) : y > x – 1}

3 . Find the inverse of the following relation represented in pictorial diagram

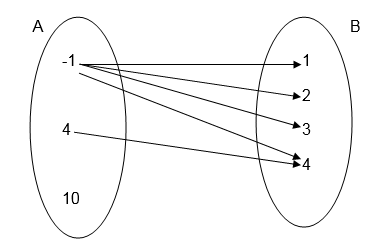
4 . State the domain and range for the relation given in question 3 above

5. State the domain and range of the inverse of the relation given in question 1 above.

A Graph of the Inverse of a Relation

Draw a graph of the inverse of a relation

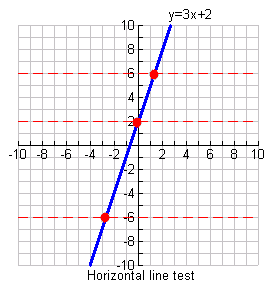
Use the horizontal line test to determine if a function has an inverse function.

If ANY horizontal line intersects your original function in ONLY ONE location, your function has an inverse which is also a function.

The function y = 3x+ 2, shown below, HAS an inverse function because it passes the horizontal line test.

Revision Questions

1. Draw the graph of the inverse of R = {(x,y) : y ≥ 0 and y ≤ x}. Find its domain and range.

Soln.

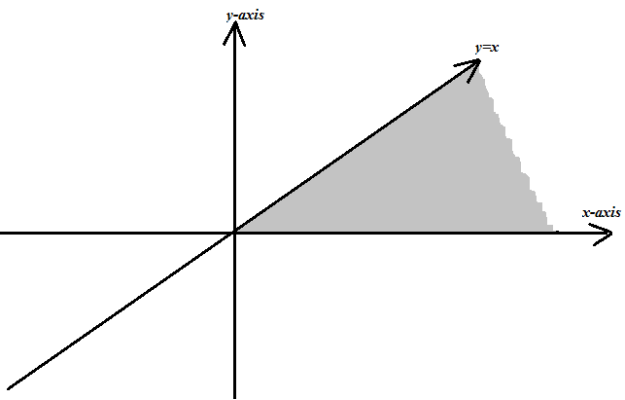
Domain={x: x ≥ 0 }

Range= {y : y ≥ 0 }

2. Given the relation;

(i)Sketch the graph of R.

(ii)State its domain and range.

(iii)Find inverse of relation R

Soln.

Given the relation;

(i)Consider the following graph of R

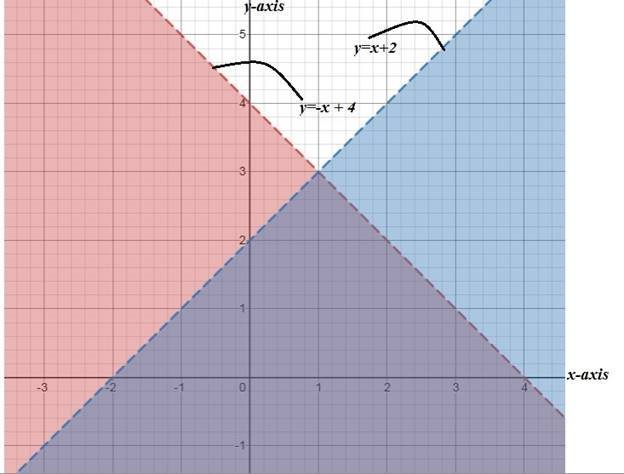
(ii)Domain = {R(x,y): All real numbers }

Range={R(x,y) : All real numbers : y< 3 }

(iii)Inverse of R

To find inverse, interchange variables of x and y

Therefore,