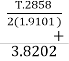CHAPTER 01 : EXPONENTS AND RADICALS
By End Of This Topic, You should be able to:
- List and Verify The laws of exponents.
- Apply laws of exponents in computations
- Simplify radicals and Perform basic operations on radicals
- Rationalize the denominator
- Read square roots and cube roots of numbers from mathematical tables
- Make one letter the subject of the formula and transpose a formula with square roots and powers
EXPONENTS
Exponents tell how many times to use a number itself in multiplication. There are different laws that guides in calculations involving exponents. In this chapter we are going to see how these laws are used.
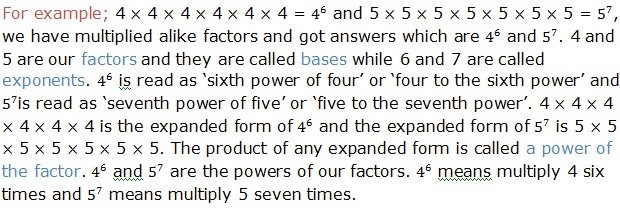
Indication of power, base and exponent is done as follows:
![]()
Solution:

To write the expanded form of the following powers:
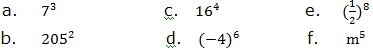
Solution
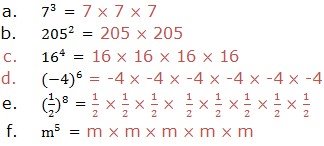
To write each of the following in power form:
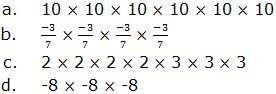
Soln.
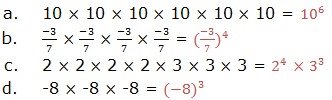
The Laws of Exponents
List the laws of exponents
First law:Multiplication of positive integral exponent
![]()
Second law: Division of positive integral exponent
![]()
Third law: Zero exponents
![]()
Fourth law: Negative integral exponents
![]()
Verification of the Laws of Exponents
Verify the laws of exponents
First law: Multiplication of positive integral exponent
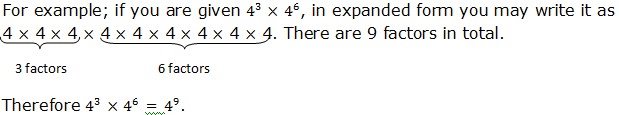
Generally, when we multiply powers having the same base, we add their exponents. If x is any base and m and n are the exponents, therefore:
![]()
Example 1
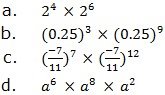
Solution
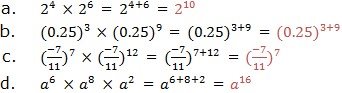
If you are to write the expression using the single exponent, for example,(63)4.The expression can be written in expanded form as:
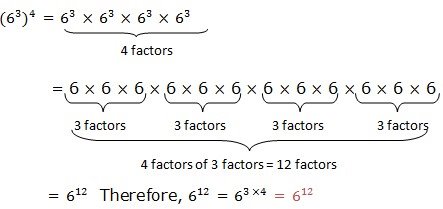
Generally if a and b are real numbers and n is any integer,
![]()
Example 2
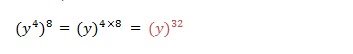
Example 3
![]()
Example 4
![]()
Generally, (xm)n = X(mxn)
Example 5
Rewrite the following expressions under a single exponent for those with identical exponents:
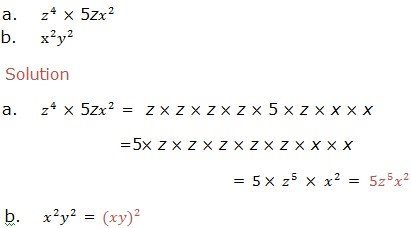
Second law: Division of positive integral exponent
Example 6
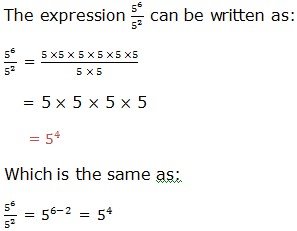
Example 7
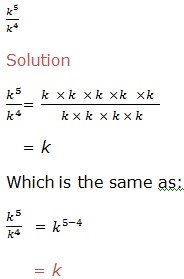
Therefore, to divide powers of the same base we subtract their exponents (subtract the exponent of the divisor from the exponent of the dividend). That is,
![]()
where x is a real number and x ≠ 0, m and n are integers. m is the exponent of the dividend and n is the exponent of the divisor.
Example 8

solution
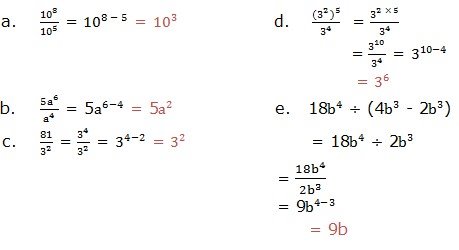
Third law: Zero exponents
Example 9
![]()
This is the same as:
![]()
If a ≠ 0, then
![]()
Which is the same as:
![]()
Therefore if x is any real number not equal to zero, then X0 = 1,Note that 00is undefined (not defined).
Fourth law: Negative integral exponents

Also;

Example 10

Exercise 1
1. Indicate base and exponent in each of the following expressions:

2. Write each of the following expressions in expanded form:

3. Write in power form each of the following numbers by choosing the smallest base:
| a. | 169 |
| b. | 81 |
| c. | 10,000 |
| d. | 625 |
a. 169 b. 81c. 10 000 d. 625
4. Write each of the following expressions using a single exponent:

5. Simplify the following expressions:
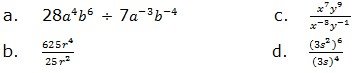
6. Solve the following equations:
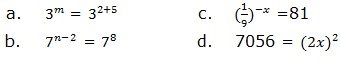
7. Express 64 as a power with:
| 1. | Base 4 |
| 2. | Base 8 |
| 3. | Base 2 |
Base 4 Base 8 Base 2
8. Simplify the following expressions and give your answers in either zero or negative integral exponents.
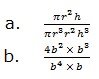
9. Give the product in each of the following:

10. Write the reciprocal of the following numbers:

Laws of Exponents in Computations
Apply laws of exponents in computations
Example 11

Solution
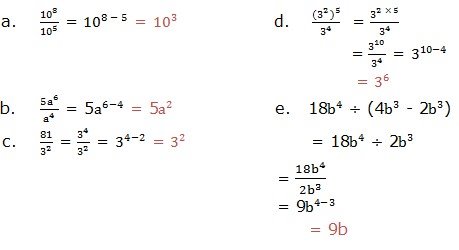
Radicals
Simplify radicals
Radicals are opposite of exponents. For example when we raise 2 by 2 we get 4 but taking square root of 4 we get 2. The same way we can raise the number using any number is the same way we can have the root of that number. For example, square root, Cube root, fourth root, fifth roots and so on. We can simplify radicals if the number has factor with root, but if the number has factors with no root then it is in its simplest form. In this chapter we are going to learn how to find the roots of the numbers and how to simplify radicals.
When a number is expressed as a product of equal factors, each of the factors is called the root of that number. For example,25 = 5× 5;so, 5 is a square root of 25: 64 = 8× 8; 8 is a square root of
64: 216 = 6 ×6 ×6, 6 is a cube root of 216: 81 = 3 × 3 ×3 ×3,3 is a fourth root of 81: 1024 = 4 ×4 ×4 ×4 ×4, 4 is a fifth root of 1024.
Therefore, the nth root of a number is one of the n equal factors of that number. The symbol for nth root isn√ where√is called a radical and n is the index (indicates the root you have to find). If the index is 2, the symbol represents square root of a number and it is simply written as√without the index 2.n√pis expressed in power form as,
![]()
nth root of a number by prime factorization
Example 1, simplify the following radicals

Solution

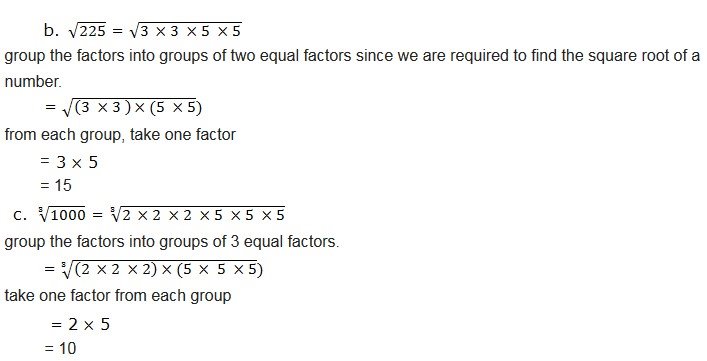
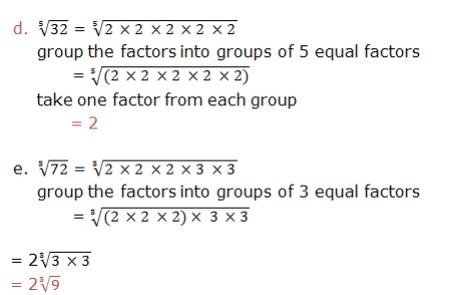
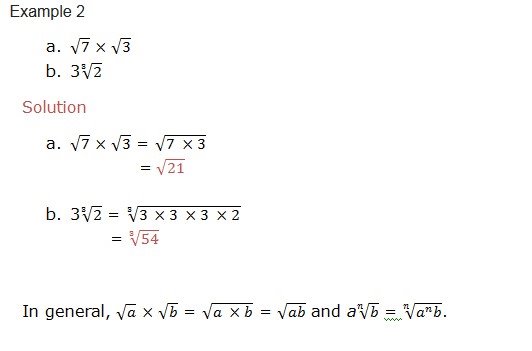
Basic Operations on Radicals
Perform basic operations on radicals
Different operations like addition, multiplication and division can be done on alike radicals as is done with algebraic terms.
Simplify the following:
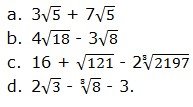
Solution
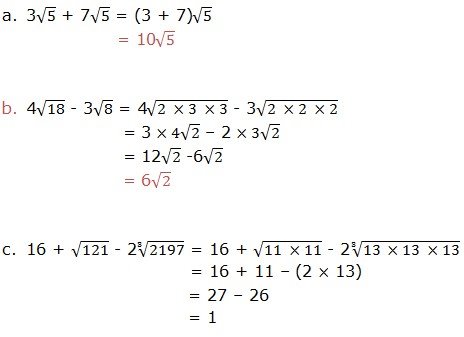
Simplify each of the following expressions:
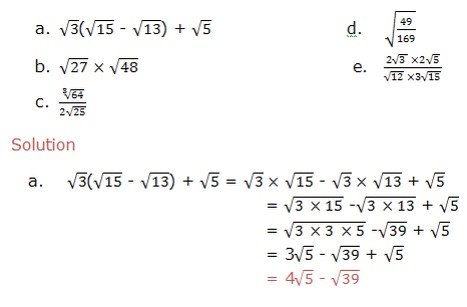

group the factors into groups of two equal factors and from each group take one of the factors.
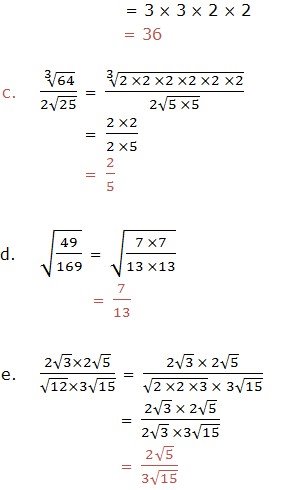
The Denominator
Rationalize the denominator
If you are given a fraction expression with radical value in the denominator and then you express the expression given in such a way that there are no radical values in the denominator, the process is called rationalization of the denominator.
Example 12
Rationalize the denominator of the following expressions:

Example 13
Rationalize the denominator for each of the following expressions:

Solution
To rationalize these fractions, we have to multiply by the fraction that is equals to 1. The factor should be considered by referring the difference of two squares.




Exercise 2
1. Simplify each of the following by making the number inside the radical sign as small as possible:


Square Roots and Cube Roots of Numbers from Mathematical Tables
Read square roots and cube roots of numbers from mathematical tables
If you are to find a square root of a number by using Mathematical table, first estimate the square root by grouping method. We group a given number into groups of two numbers from left. For example; to find a square root of 196 from the table, first we have to group the digits in twos from left i.e. 1 96. Then estimate the square root of the number in a group on the extreme left.
In our example it is 1. The square root of 1 is 1. Because we have two groups, this means that the answer has two digits before the decimal point. Our number is 196, read 1.9 in the table on the extreme left. From our number, we are remaining with 6, now look at the column labeled 6. Read the number where the row of 1.9 meet the column labeled 6. It meets at 1.400. Therefore the square root of 196 = 14.00 since we said that the answer must have 2 digits before decimal points. Note: If you are given a number with digits more than 4 digits. First, round off the number to four significant figures and then group the digits in twos from left. For example; the number 75678 has five digits. When we round it off into 4 digits we get 75680 and then grouping into two digits we get 7 56 80. This shows that our answer has 3 digits. We start by estimating the square root of the number to the extreme left, which is 7, the square root of 7 is between 2 and 3. Using the table, along the row 7.5, look at the column labeled 6. Read the answer where the row 7.5 meets the column 6. Then go to where it is written mean difference and look at the column labeled 8, read the answer where it meets the row 7.5. Take the first answer you got where the row 7.5 met the column 6 and add with the second answer you got where the row 7.5 met the column 8 (mean difference column). The answer you get is the square root of 75680.
Which is 275.1
Transposition of Formula
Re-arranging Letters so that One Letter is the Subject of the Formula
Re-arrange letters so that one letter is the subject of the formula
A formula is a rule which is used to calculate one quantity when other quantities are given.
Examples of formulas are:

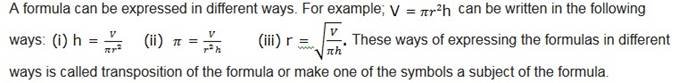
Example 14
From the following formulas, make the indicated symbol a subject of the formula:
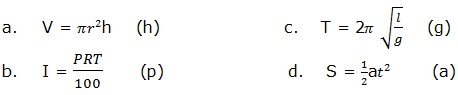
Solution

Transposing a Formulae with Square Roots and Square
Transpose a formulae with square roots and square
Make the indicated symbol a subject of the formula:
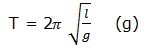
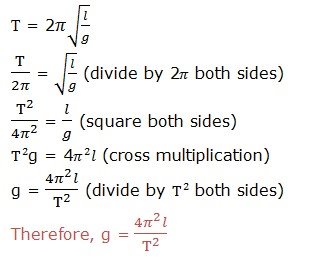
Exercise 3
1. Change the following formulas by making the given letter as the subject of the formula.
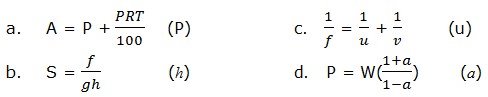
2. Use mathematical tables to find square root of each of the following:

REVISION QUESTIONS
1. Simplify
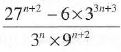
Ans.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. By rationalizing the denominator, simplify the following expression.
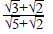
Ans.
![]()
![]()
![]()
![]()
3. Find the value of x for which 2x ? 16 = 81x
Ans.
2x.16=![]()
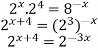
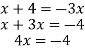
X=-1
4. Rationalize ![]()
Ans
Rationalize
![]()
Rationalizing the denominator we get
![]()
![]()
![]()
5. By using mathematical tables, evaluate 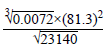 to three significant figures.
to three significant figures.
Ans.
Let x =![]()
Apply log sides
Log x=![]()
=log ![]()
=![]()
By using Four figures Mathematical tables
| Number | Log |
|
|
|
| Numerator | 3.1060 |
|
|
2.1822 |
|
|
|
| 8.39 x 10° | 0.9238 |
6. Simplify ![]() by rationalizing the denominator.
by rationalizing the denominator.
Ans
![]()
![]()
![]()
![]()
7. Solve for x if ![]()
Ans.
![]()
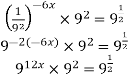
![]()
![]()
![]()
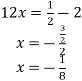
8. (i) Express (?3 + 5)2 in the form a + b?3, where a and b are integers.
(ii) Express
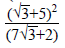
in the form p + q?3, where p and q are rational numbers.
Ans
(i)![]()
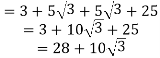
(ii) From ![]() part (i) above
part (i) above ![]()
Rationalizing the denominator,
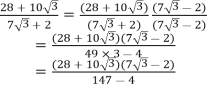
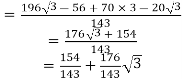
9. Solve the value of x if
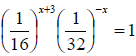
Ans.
![]() 1marks
1marks
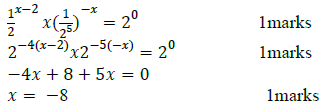
10. Find the value of x and y if
![]() = 2025
= 2025
Ans.
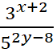 = 2025
= 2025
But 2025=3x3x3x3x5x5
![]() =
=![]()
![]()
So ![]() =
= ![]()
![]() =
= ![]()
Then x=2 and y=3
11. Find the value m + n, given that 7m × 5n = 875 .
Soln.
Given, 7m x 5n = 875 but 875 = 7 x 125 7m x 5n = 7 x 125
125= 5 x 5 x 5 =53
7m x 5n =71 x 53
Now compare exponents with the same base
Hence, m=1 and n=3 m + n= 1 + 3 =4 Therefore, (m+ n) =4
12 Which numbers are equal to their squares?
Soln.
Numbers are equal to their squares are 0 and 1.
13. Simplify the expression ![]()
Soln.
![]()
![]()
14. Rationalize the denominator of the expression
![]()
Ans.
Given
![]()
To rationalize the denominator, multiply by ![]() both in numerator and denominator
both in numerator and denominator
![]()
![]()
![]()
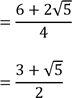
15. Express in decimal notation ![]() percent of
percent of ![]()
Ans.
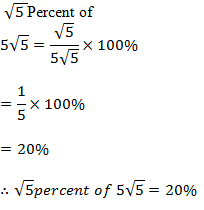
16. Express R as the subject of ![]()
Ans.
Given ![]()
V (r +R) =12R
Vr+YR=12R
Vr+YR=12R
Vr=12R – VR
17. If ![]() determine the value of
determine the value of ![]()
Ans
8. Given a2=12 a4=? a4=(a2)2
But a2 =12
Thus a4 = (12)2
a4=144
18. Simplify (-4g5)3
Soln.
(-4g5)3 = (-4)3 g8
(-4g5)3 = -64g8
19. Rationalize the denominator to the simplest form:
![]()
Soln.
To rationalize the denominator, multiply by ![]() both in numerator and denominator
both in numerator and denominator
![]()
![]()
![]()
20. Express the equation ![]() = 1 in terms of P given that P = 3y.
= 1 in terms of P given that P = 3y.
Soln.
To write 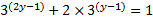
in term of P given that ![]()
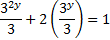
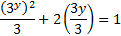
But ![]()
![]()
Multiply by 3 both sides
3x![]()
![]()
![]()
21. Find the value of x in the equation ![]()
Soln.
Given
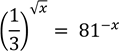
![]()
![]()
Since bases are the same, compare exponent
![]()
![]()
Square both sides
X = 16x2
x-16x2 =0
x(1 - 16x)=0
x= 0 or 1-16x=0
x=0 or x=1/16
22. Solve for x in the equation 4-2x × 82 = 4 × 16x .
Soln.
4-2x x 82 =4 x 16x
2-4x x 26 =22 x 24x
2-4x+6 = 22+4x
Since bases are the same, now compare the exponents
-4x+6=2+4x
4x+4x=6 - 2
8x =4, divide both sides by 8
Therefore, x=0.5
23. Solve for x in the equation 9(x-3) × 81(1-x) = 27-x .
Soln.
Given Eqn. 9(x-3) × 81(1-x) = 27-x .
32(x-3) × 3 4(1-x) = 3-3x .
3(2x-6 +4 - 4x) = 3-3x
3(-2x - 2) = 3-3x
Since base are the same, now compare the exponents
-2x-2=-3x
3x-2x=2
x=2
Therefore, x=2.
24. Simplify the expressions:
(i) ![]()
![]()
Soln.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
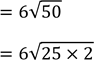
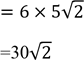
25. Find the values of x and y if
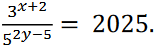
Soln.
![]()
2025=81 x 25= 34 x 52
![]()
From Equation above, compare exponents of the same base
-(2y-5)=2
-2y+5=2
-2y=-3
y=3/2
x+2=4
x=4-2=2
![]()
26. Solve equation ![]()
Soln.
![]()
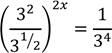
![]()
![]()
![]()
Since base are the same, now compare the exponents
3x= -4
x =-4/ 3= -4/3
27. If ![]() , find the values of a, b and c.
, find the values of a, b and c.
Soln.
To get the value of a, b and c we have to rationalize the denominator
![]()
![]()
![]()
![]()
![]()
From comparison above, a= -3, b=2 and c=3
28. Rationalize the denominator of the expression
![]()
Soln.
To rationalize the denominator, we've to multiply the given expression by ![]() in both numerator and denominator
in both numerator and denominator
![]()
![]()
![]()
Therefore
, ![]()
![]()
29. If ![]()
Find values of x and y
Soln.
Given
![]()
![]()
![]()
From the above, compare exponents with the same base
![]()
x+3=-5 x=-5 -3 =-8 Therefore, x =-8
![]()
2 -y = -1
-y = -1 - 2 =-3
-y = -3, y=3
Therefore, y =3
30. Solve for n
![]()
Soln.
Given
![]()
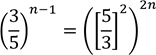
![]()
![]()
Since base are the same, now compare exponents
4n= 1 - n
5n =1
n = 1/5
31. Use laws of exponents to simplify
![]()
Ans.
![]()
![]()
![]()
![]()
32. Rationalize the denominator of
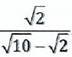
Soln
Given
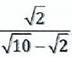
To rationalize the denominator, multiply by 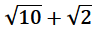 in both numerator and denominator
in both numerator and denominator
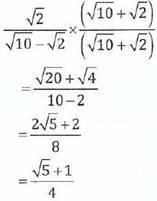
33. Find the value of x in the equation 9x34x =27(x-1)
Soln.
Given 9x34x =27(x-1)
32 x 34x = 33(x-1)
From laws of Exponent; ax x ay=a(x+y)
3(2+4x) =33(x-1)
Since bases are the same, now compare the exponents
(2+4x) =3(x-1)
2+4x =3x - 3
4x - 3x=-3 -2
x= -5
34. Without using mathematical tables, evaluate: .
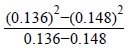
Soln.
Given:
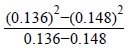
Recall Concept Of Difference of Two Square That: a 2 - b2 =(a +b)x (a - b)
![]()
= (0.136 + 0.148)
![]()
35. Find the value of ![]() given that 3a x 5b = 675
given that 3a x 5b = 675
Soln.
Given 3a x 5b = 675 but 625 = 25 x 27
625 =52 x33
Now,
3a x 5b =33 x 52
Now compare
3a = 33 , therefore a=3
5b = 52, therefore b= 2
Hence
![]()
36. Solve for n in the equation ![]() =1/2
=1/2
Soln.
Solve for n
![]()
By comparing exponents since base are the same
4(3-n) +(1+n)= -1
12- 4n +1+n =-1
13- 3n =-1
13+1 = 3n
14 = 3n
![]()
37. ![]()
Soln.
To find x, take 9 to the R.H.S
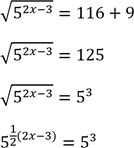
since base are the same, now compare the exponents
![]()
(2x-3)=6
2x=6+3
2x=9
Therefore: ![]()
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
WHATSAPP US NOW FOR ANY QUERY
App Ya Learning Hub Tanzania