CHAPTER 1: NUMBERS

The student should be able to:

• identify the place value in each digit in base ten numeration.
• read numbers in base ten numeration AND write numbers in base ten numeration up to one billion
• distinguish between natural and whole numbers AND identify even, odd and prime numbers
• add , subtract, multiply and divide whole numbers.
• find factors of a number, multiples of a number , and use factors and multiples of number to find G.C.F and L.C.M of numbers
• identify integers, add, subtract, multiply and divide integers and perform mixed operations on integers

What is numbers?

Numbers are symbols or words which represent quantity of something for example in form 1B there are forty four students.

i.e. 44 students

The numbers are represented by symbols called numerals.
Each symbol in a numeral is called a digit.
E.g. In 256 there are three digits 2, 5, and 6.
There are ten digits which are 0, 1, 2, 3, 5, 6, 7, 8, and 9

Each digit in a numeral has a value called place value.
Example in 316, 6 is called ones and can be written as 6 1 , 1 is called tens and is written as 1 10 and 3 is called hundreds written as 3 100.
Therefore 316 can be written as 3 100 +1 x 10 + 6 1 this form is called expanded form.

The system where numbers are in groups of ten is called base ten numerations or decimal system numeration.The place value of every digit in decimal system numeration is ten times the place value of the next to the right.

Table of place values:-

Exercise 1.1

1. Write each of the following numbers in expanded form:-

(a) 94 =

(b) 7019 =

(c) 50 =

(d) 303 =

(e) 5003 =

(f) 500 =

(g) 999 =

(h) 5 =

(i) 5000 =

2. Find the place value of the following:-

(a) 513 (1)

The place value of 1 is

(b) 357999 (5)

The place value of 5 is

(c) 50149 (5)

The place value of 5 is

(d) 8665 (8)

The place value of 8 is

(e) 227 (7)

The place value of 7 is

(f) 900412 (4)

The place value of 4 is

3) Write the numerals for each of the following:-

(a) 9 100 + 0 10 + 1 1

(b) 5 10000 + 5 1000 + 5 100 + 5 10 + 5 1

(c) 6 100000 + 8 10000 + 0 1000 + 1 100 + 7 10 + 0 1

(d) 5 100 + 0 10 + 1 1

1:2 NATURAL AND WHOLE NUMBERS

Natural numbers

Natural numbers are the ones that begin with 1,2, 3 to infinity.

They are counting number, they are denoted by N

Number line of natural numbers.

Whole numbers

Are the ones that begin by 0, 1, 2, 3, to infinity? They are denoted by W, in a number line.

Even, odd and prime numbers:-

Even: are natural numbers which are divisible by 2 without remainder.

Example: - 2, 4, 6, 8, 10, 12.

Odd:-

Odd numbers are natural numbers which are not divisible by 2, when they are divided by 2 they give remainder, so the answer is not a natural numbers.

E.g: 1, 3, 5, 7, 9, 11…………………………………………

Prime numbers:-

Prime numbers are natural numbers which are divisible by one and by themselves. They are the ones with only two factors.

E.g. 2, 3, 5, 7, 11, 13 …………………..

Numbers up to one billion:

Ten	10
Hundred	100
Thousand	1,000
Ten thousand	10,000
Hundred thousand	100,000
One million	1,000,000
Ten million	10,000,000
Hundred million	100,000,000
One billion	1,000,000,000

EXERCISE 1:2

1. For the given numbers below, write down which are:-

(a)Even (b)Prime (c)Odd
9,12,15,17,25,36,37,38,39,40,41,42,43,44,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71.

2. Write down the prime numbers between 70 and 90.

3. Write down a number which is even and prime

4. Among the numbers 3, 5, 7, 9, 11, 13.What is not a prime number?

5. Show even, odd, and prime numbers less than 10 on separate number

6. (a) Given any point as a number on a number line for N or W.

Can you always name another one to the right of it?

7. Given any two points as numbers one after another on a number line for N or W. Can you find the whole numbers between them?

8. Do the points representing N and W on a number line completely fill the number line?

9. How does N differ from W.

More examples

1. Write the following numerals in words:-

(a) 72 - Seventy two

(b) 10368 - Ten thousand three hundred and sixty eight.

(c) 1152 - One thousand one hundred and fifty two.

(d) 144 - One hundred and forty four.

(e) 573921 - Five hundred and seventy three thousand nine hundred and twenty one

(f) 952675 - Nine hundred and fifty two thousand six hundred and seventy five

(g) 105, 451, 225 - One hundred and five million, four hundred and fifty one Thousand, two hundred and twenty five

2. Express the statement in numerals:-

Nine billion eight hundred million and two hundred = 9,800,000,200.

3. Write down the largest four digit number = 9,999.

4. Write down the largest four digit number when the digits are not repeating =9876.

5. Write down the smallest three – digit number without using a zero = 111

6. Change the order of the digits in 47986 to make:

(a) The largest possible number = 98764

(b) The smallest possible number = 46789

7. Write down the number with 6 in the hundred place, 9 in the tens place, 0 in the thousands place, 4 in the units place and 3 in the ten thousands place. 30,694

8. Write down next three counting numbers after 6999.

7000, 7001, 7002

9. Write the numbers in words:-

(a) 6054 - Six thousand and fifty four

(b) 3,250,000 - Three million two hundred and fifty thousand.

(c) 106,000 - One hundred and six thousand

(d) 100,600 - One hundred thousand and six hundred.

(e) 100,006 - One hundred thousand and six.

(f) 205,020 - Two hundred and five thousand and twenty.

(g) 2,415,982,728 - Two billion, four hundred and fifteen million, nine hundred and eighty two thousand, seven hundred and twenty eight.

10. Write in numerals:-

(a) Six hundred seventy five -675

(b) Four hundred and five - 405

(c) Three thousand and sixteen - 316

(d) Eight thousand and sixteen - 8016

(e) One hundred thirty seven thousand two hundred and fourteen – 137214

(f) One million five hundred thousand - 1,500,000

(g) Two million twenty three - 2,000,023

(h) Nineteen thousand and forty five - 19,045

(i) One billion fourteen million two hundred and fifteen thousand - 1,014,215,000

Operations with whole numbers:-

There are four operations which are addition, subtraction , multiplication and division.

Addition (plus) (+):-

Horizontal addition

E.g. 254 + 369 =623

14796 + 230 + 14 =15030

Vertical addition:-

The answer obtained after adding is called sum.

Subtraction ( - ) (minus):-

Horizontal subtraction

E.g. 2349610 - 1396789 =952821

129 - 98 =31

The answer obtained after subtracting numbers is called Difference.

Vertical subtraction:-

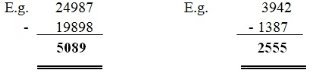
Multiplication /Times (x)

a b = c

a = Multiplicant

b = Multiplier

c = Product

There are two types of Multiplication

Horizontal multiplication

E.g 2486 7 = 17402

E.g 126 8 = 1008

Vertical – multiplication:-

The number that multiplies is called Multiplier
The number to be multiplied is called multiplicand
The answer obtained after multiplication is called product.

DIVISION (÷)
a÷b=c
a = dividend

b = divisor

c = quotient

Short division

Long or vertical division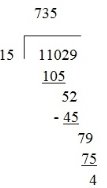



Q = 735 remainder 4

The number that divides is called divisor

The number to be divided is called dividend.

The answer obtained after division is called Quotient.

The left over upon division is called Remainder.

e.g. 29 ÷ 6 =

Word problems on whole numbers

1. E.g In a school garden there are four rows of cabbage with 12 in each row, six rows of tomatoes with eight in each row.

How many plants of each kind are there?

Solution:-

1 row = 12 cabbage

4 rows = x

x = 12 cabbages x 4 rows

x = 48 cabbages

1 row = 8 tomatoes

6 row = x

X = 8 tomatoes x 6 rows

X = 48 tomatoes

There are 48 cabbages plants

48 tomatoes plants

2. Two thousand four hundred shillings are deposited by a teacher each month, How much is this after two years?

Solution:-

2400shs = I month

1 year = 12 months

2 yrs = 24 months

2400shs x 24 months

∴ = 576000/=

More examples

2. 28782 - 2784 + 294.

Solution:-

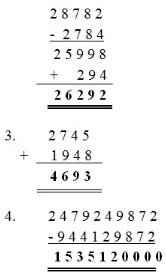
Will the sums of the following be even or odd:-

5. Two numbers which are Odd.
The answer must be even.

6. Two numbers which are even.

Even numbers

7. An odd and even number

Odd numbers

8. Any two odd numbers.

Even numbers

9. Use horizontal way to find products in questions:-

1. 128 x 5 = 640
2. 195 9 = 1755
3. 17289 2 = 34578

10. Use long multiplication method to evaluate:-

249752 8921

Solution:-

11. Find the product and quotient of the following

(a) 247 x 100

Soln:-

Revision exercise

1. In a school garden there are 4 rows of carrots with 10 in each row .

How many plants are there?

2. Six students were given 96,000 shillings to share equally. How many shillings did each student get?

3. The cost of one kilogram of sugar is 700 shillings and Juma buys 8 kgs of sugar.

How much did cost him?

4. Richard sold 240 copies of the daily news paper for 300 shillings each, 198 pieces of the Uhuru news paper for 200 shillings and 6 sports magazine for 500 shillings each. How much did he collect in all?

5. There are 17 streams in a school, each stream has 35 pupils. How many pupils are there in the school.

6. A page of a book has 36 lines. If each line contains 14 words, how many words are these if the book has 250 pages?

7. Jim’s school is 13 km from his home. If he goes to school daily how many kilometers does he travel in 196 days.

8. Each day a school shop collects sh. 75000 from the customers. If the collection was made for eight days and sh. 275000 of the collected money was used to make a fence for the school. How much money was left?

9. A school collects 140 eggs from its poultry farm each day. Each egg costs 80shillings. How much money per day does the school earn in selling the eggs?

10. A school of 900 students has decided to make uniforms for each student. If a shirt and a pair of trousers need 2 m and 1.5 m respective, How much of each material of cloth will the school need so as to give uniforms to all students.

SOLUTIONS

Qn 1.

Qn 2.

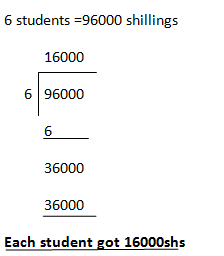
Qn 3.


Qn 4.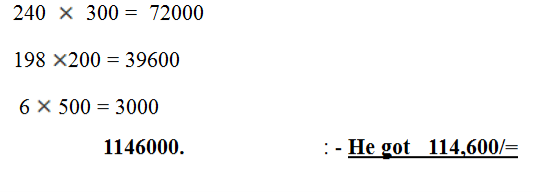

Qn 5.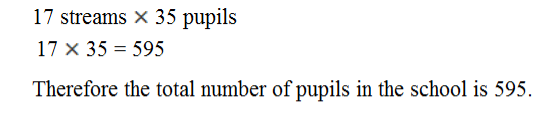

Qn 6.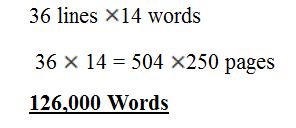

Qn 7.

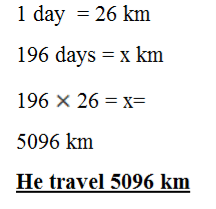
Qn 8.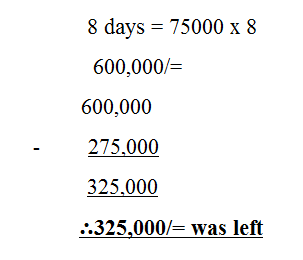

Qn 9.
Qn 10.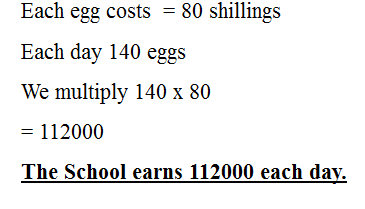


ORDER OF OPERATIONS
The order of priority is often given by the word BODMAS to mean

B rackets
O rders
D ivision
M ultiplication
A ddition
S ubtraction
so first perform any operation in brackets, Then any use of orders division or multiplication followed by Addition or subtraction
Example : evaluate the following

(a) 12 + 4 x2 = 12 + (4x2)
= 12 + 8
12 + 4 x 2 = 20

(b) 20 ÷ 2 + 3 = (20 ÷ 2) + 3
= 10 + 3
20÷2 + 3 = 13
(c) 4 x 3 + 7 x 2 = (4 x3) + (7 x2)
= 12 + 14
= 26

1:4 FACTORS AND MULTIPLES OF NUMBERS

When a number divides exactly into another number, it is called a factor of a second number.

The second number is called a multiple of the first numbers.

e.g 16 ÷ 8 = 2 So 2 is the factor of 16 and 16 is the multiple of 2. Other factors of 16 are 8, 4, 1 and 16.

In general one (1) is a factor of every number and each number is a factor of itself.

- Factors of a number are numbers less than the given number.

- Factors are finite, and divisors of the given number.

- Multiple are number greater than the given number.

-They are infinite and dividend of a particular number.

E.g Factors of 36 = 1, 2, 3, 4, 5, 6, 9, 12, 18, and 36
Multiple of 3=3,6,9,12,15,18,21,242,730.............

PRIME FACTORIZATION

Is the process of writing numbers using their prime factors we use the short division in writing / factorization.

E.g Write the following as the product of their prime factors.

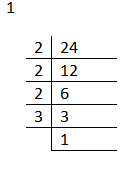∴24=2×2×2×3

∴48=2×2×2×2×3

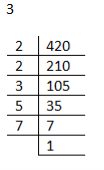∴420=2×2×3×5×7

∴360=2×2×2×3×3×5

THE LOWEST COMMON MULTIPLES (LCM)

LCM is the short form of lowest or least common multiple .

E.g 2 = 2, 4 6 8 , 10, 12, 14, 16, 18, 20, 22, 24-……………

3 = 3, 6, 9, 12 15, 18, 21, 24 27, ……………….

Common multiples are = (6, 12, 18, and 24)

LCM = 6

E.g Find the lowest common multiples of 9, 18, 24

Soln

9 = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126………….

18 = 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, 198…………………………

27 = 27, 54, 81, 108, 135, 162, 189………………………………….

Common multiples are={54,108....}
The least common multiples=54

PROPERTIES OF WHOLE NUMBERS

There are five properties of whole numbers.

1. Closure property (law)

When two or more whole numbers are operated by adding or multiplying the answer is also a whole numbers.

That is if a and b are whole numbers. Then a + b = c. C is also a whole number. a x b = d d is also a whole number.

E.g 4 + 6 = 10

3 5 = 15

2. Commutative property:-

If a and b are whole numbers.

Then (i) a + b = b + a

(ii) a b = b a

E.g 3 + 4 = 7

4 + 3 = 7

Implies: 3 + 4 = 4 + 3

a+b=b+a

9 6 = 54

6 9 = 54

a b = b a

3. Association property:-

If a + b & c are whole number.

Then (i) (a + b) + c = a + (b + c)

(ii) (a b) c = a ( b x c)

E.g (2+3)+4=5+4
=9
2+(3+4)=2+7
=9

Implies: (2+3) + 4 = 2 + (3 + 4)
(a + b) + c = a + (b+c)

E.g. (4 2) 5 = 8 5
= 40
4 (25) = 4 10
=40

Implies (4 2) 5 = 4 (2 5)
(a x b) x c = a x (b x c)

4. Distributive property:-

If a, b, and c are whole numbers, then
a x (b+c) = (a b) + (a c)

E.g 4 (6 + 9) = 4 15 = 60
4(6+9)=(4×6)+(4×9)
=24+36
=60

Implies: 4 (6 9) = (4 6) + (4 9)
a x (b+c) = (a b) + (a c)

5. Identity property:-

If A is a whole number,

Then (i) a + 0 = 0 + a = a

0 is called an identity of addition

(ii) a 1 = 1 a = a

1 is called and identity of multiplication.

Exercise 1:5
1. Match the property in left column and right column then name the property

Left hand column Right hand column

(a) 2 + (3 +5) (h) (2+3) + 5

(b) 1+ (2 +3 ) (i) (2 + 2) + 1

(c) 2+ (2 +1 ) (j) (8 +4 ) + 4

(d) 4+ (3 +5 ) (k) (1 + 2 ) + 3

(e) 1 + (1 +3) (l) (3 + 5) + 4

(f) 8 + (4 +4) (m) (1 + 1) + 3

(g) (1 + 3) + 1 (n) 1 + (1 + 3)

solution

a and h have Associative property

b and k have Commutative property

c and I have Associative property

e and m have Commutative property

f and j have Associative property

g and n have Commutative property.

2. By using properties of whole numbers give reasons why each of the following two expressions are equal.

(a) 5 + (6 + 7) = (7 + 6) + 5

- The answer to the two expressions will be the same because they numbers have commuted.

(b) (8 + 3) + 4 = 8 + ( 4 + 3)

- When you solve this you will get the same answer because of the exchange of the numbers.

(c) 5 + (2 + 1 ) = 1 + ( 3 + 2)

- In this expression, we have seen that they are two different expressions so you cannot get the same answer from the two.

(d) (5 + 3) + 2 = 3 + ( 2 + 5)

- In this two expression you can get the same answer because only the position of numbers and brackets as the one that has changed.

3. Telling / writing equal expressions;-

(a) 2 (5 3) = (2 5) 3 - Associative property

(b) 4 (3 5) = (4 3) 4 - Associative property

(c) 2 (4 7) = 7 (2 4) - Associative property

(d) 3 (2 2) = 3 (2 2) 3 - Commutative property

(e) (3 2) 6 = 16 (2 2) - Commutative property

(f) (3 2) 3 = (2 3) 3 - Commutative property

4. Why is it permitted to write 3 x 2 x 5 x 9 without any brackets?

Because even if they are written without brackets they don’t destroy the meaning of the question / statement.

5. Express each of the following in the form of (a x b ) + (a x c)

(a) 2 (3 + 5)
= (2 3) + 2 5)

(b) 4 (3 + 10)
= (4 3) + 4 10)

(c) 2 x(3 + 7)
= (2 3) + 2 7)

(d) 4 (3 + 1)
= (4 3) + 4 1)

6. Express each of the following in the form a x (b + c)
(a) (2 5 ) + 2 3)
= 2 (5 + 3)

(b) (5 3) + 5 7)
= 5 (3 + 7)

(c) (2 1) + (2 3)
= 2 (3 + 7)

(d) (7 3) + (7 1)
= 7 ((3 + 1)

7. Calculate the following:-

(a) 14 5 + 16 – 4 = 82

(b) 36 72 ÷ 4 = 648

(c) (144 + 20) x 48 + 4 ÷ 2 = 7872

(d) 24 (10 + 54) + 8 = 192.

1:5 INTEGERS

The integers are whole numbers from negative infinity to positive infinity. They are denoted by Z.

The order of the size of the number 1, 2, 3, 4……. Can be represented as points on a number line

Starting from 0 to the right and other numbers from 0 to the left

Number line for Z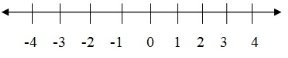

If we want to know which number is larger than the other we have to consider which one is to the right or left

Consider the following

e.g. write down all the integers between -5 and 4

Solution

Example: present on a number line

-3 Z 5

-2 -1 0 1 2 3 4

-3 Z 5

-3 -2 -1 0 1 2 3 4

Operation with integers

Integers can be operated using number lines except for division

Addition

Addition of integers

RULE1:To add a negative integer you move to the left on the number line.
Example
-2+-5=-7
Start at -2 move 5 steps to the left or Star at 0 move 2 steps to the left then-5 steps to the left

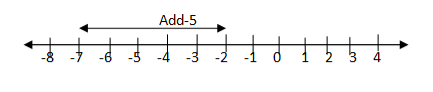
OR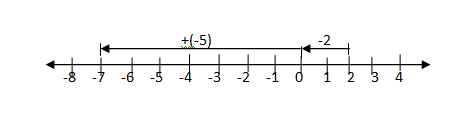


RULE2:To add a positive integer you move to right on number line.
Example
-4+(+6)=+12
Start at -4 move 6 steps to the right

OR
Start at 0 move 4 steps to the left then 6t steps to the right

+3+(+4)=7
Start at +3 move 4 steps to the right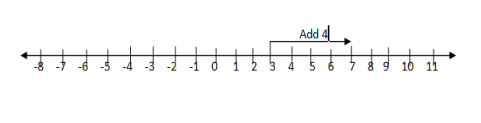

-4+-6=-10
Start at -4 move 6 steps to the left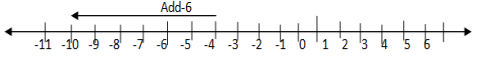

Subtraction of integers
Subtraction of positive integers gives the same result as addition of integers
RULE 1
To substract a positive integer you move to the left on the number line.
Example -4-(+3)=-7
start at -4 move 3 steps to the right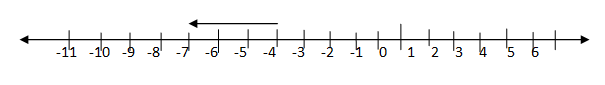

RULE2
To subtract a negative integer you move to the right on the number line
Example
-7-(-3)=-4
Start at -7 move 3 steps to the right

Multiplication
The rules for multiplying are as follows

+×+=+
+×-=-
-×+=-
-×-=+

Division
The rules for division are as follows

+ ÷ += +
+ ÷ - = -
- ÷ + = -
- ÷ - = +
NOTE: The result are similar to the rules of multiplication.
Example:
-36÷6=-6
24÷6=+4
24÷-6=-4
-24÷6=-4
-24÷-6=4

REVISION QUESTIONS

1 Find the product of the G.C.F and L.C.M of 6, 9 and 15.

Soln.

G.C.F and L.C.M of 6, 9 and 15

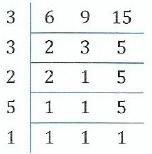
G.C.F = 3 x 1 =3

L.C.M = 3 x 3 x 2 x 5 =90

Therefore, product Of LCM and GCF =90 x 3 =270

---

2. .Write the number 2373695 in words

Soln.

Given number 2,373,695

In words

Two million, three hundred seventy three thousand, six hundred and ninety five

---

3 Find the Least Common Multiple of 24, 36 and 48.

Soln.

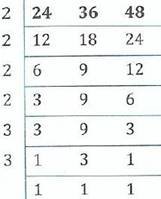
LCM= 2 x 2 x 2 x 2 x 3 x 3

Therefore, LCM= 144

---

4. If N is a number such that when multiplied by 0.75 gives 1, find the value of N

Soln.

N x 0.75 = 1

0.75N = 1

Multiply By 100 both sides

75N = 100

Divide by 75 both sides

Therefore,

---

5. The numbers 2, 3, 5 and Y have an average equal to 4. What is the number represented by the letter Y?

Soln.

Given average of 2, 3, 5 and Y is 4

Cross-multiplication

10+Y=16 Y=16 -10

Y=6

---

6 If the production of 6 integers is negative, find the maximum number of integers in that product which are negative.

Ans

Maximum number of negative integers is 5

---

7. Find the average of all multiples of ten from 10 to 190

Ans

Multiples of 10 to 190 are 10, 20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190.

Sum of those multiples

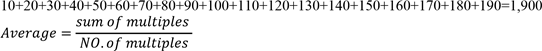
Average=100

---

8. Add the first three common multiples of 3 and 5.

Soln.

First common multiples of 3 and 5 is 15

Second common multiples of 3 and 5 is 30

Third common multiples of 3 and 5 is 45

Their summation = 15 + 30 + 45 =90

---

9. Find the lowest common multiple of the numbers 15, 35 and 40.

Ans

To find L.C.M

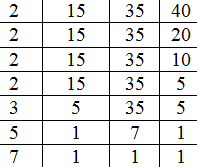
L C.M= 2x2x2x3x5x7

= 8x15x7

= 56x15

Therefore L.C.M =840

---

10. Determine the number of significant figures in each of the numbers: 400,780 and 0.00606, then approximate each number into one significant figure.

Soln.

400,780 - Has 5 significant figure

0.00606 - Has 3 significant figure

400,780=400,000 (Approx. to 1 s.g.f)

0.00606 = 0.006 (Approx. to 1 s.g.f)

---

11. Write in numerals: nine hundred ninety nine million nine hundred ninety nine thousand nine hundred and one.

Ans

Soln.

999,999,901

---

12. By using the listing method, write the lowest common multiple of 3, 10 and 15.

Soln.

3= 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, . . . . . .

10= 10, 20, 30, 40, 50, . . . . . .

15= 15, 30, 45, . . . . .

Therefore, the lowest common multiple of 3, 10 and 15 is 30

---

13. Write 498,030 in words.

Soln.

Four hundred ninety eight thousand and thirty.

---

14. Four wooden rods with lengths of 70 cm, 119 cm, 84 cm and 105 cm are cut into pieces of the same length. Find the greatest possible length for these pieces if no wood is left over.

Soln.

To get the greatest possible length, we've to calculate the Greatest Common Factors of the three length

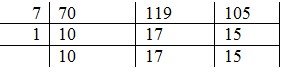
G.C.F=7 x 1=7

Therefore, the greatest possible length is 7cm.

---

15. From the set of numbers {1, 3, 4, 5, 6, 8, 10, 15, 17, 21, 27}; write down:

(i) the prime numbers, (ii) the multiples of 3, (iii) the factors of 60.

Soln.

Given set of numbers {1, 3, 4, 5, 6, 8, 10, 15, 17, 21, 27}

(i) Prime numbers are {3, 5, 17}

(ii) Multiples of 3 are {3, 6, 15, 21, 27}

(iii) Factors of 60 are {1, 2, 3, 4, 5, 6, 10, 15}

---

16. Find the GCF of 210, 357 and 252.

Soln

G.C.F of 210, 357 and 252

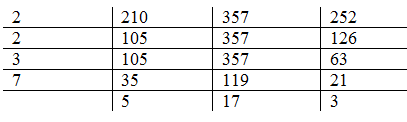
Therefore, G.C.F=3 x 7 =21

---

17. ( Three airplanes arrived at Kilimanjaro International Airport (KIA) at the intervals of 30 minutes, 40 minutes and 55 minutes. If all three airplanes arrived at KIA at 2:00 p.m. on Saturday, when and at what time would they arrive together again?

Soln.

For 3 planes to arrive together, we've to find the time interval that will take for 3-planes to arrive together by finding the LCM of 30min, 40mins and 55mins

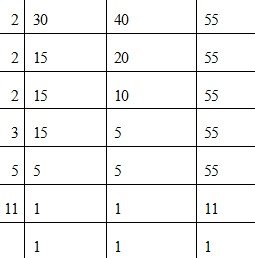
LCM = 2 x 2 x 2 x 3 x 5 x 11

LCM=1320

So it will take 1,320mins for planes to arrive together

1,320min = 22hrs

So, Saturday 2:00Pm + 22hrs =Sunday 12: 00Am Therefore, 3 planes will arrive together on Sunday 12: 00Am

---

18. Write each of the numbers 18, 24 and 36 as a product of prime factors and hence find their greatest common factor.

Soln.

18 = 2 x 3 x 3

24 = 2 x 2 x 2 x 3

36 = 2 x 2 x 3 x 3

G.C.F =2 x 3 =6

---

19. Express 0.00152 correct to:

(i) two (2) significant figures

(ii)three (3) decimal places

Soln.

Given 0.00152, correct to:

(i)two (2) significant figures = 0.0015

(ii)three (3) decimal places = 0.002

---

20. Express the numbers 1470 and 7056 each as a product of its prime factors.

Hence evaluate and simplify

if m = 1470 and n = 7056.

Soln.

Given 1470 and 7056

1470 = 2 x 3 x 5 x 7 x 7

7056= 2 x 2 x 2 x 2 x 3 x3 x 7 x7

Hence

Therefore,

---

21. A block is cut into equal units of l0g, 20g and 35g. Use prime factorization method to find the smallest possible mass of the block form which the pieces can be cut.

Soln.

By using prime factorization

10 = 2 x 5

20 = 2 x 2 x 5

35 = 5 x 7

Therefore Lowest possible mass is 2 x 2 x 5 x 7= 140g

---

22. Find the LCM and GCF of 13, 52 and 104.

Soln.

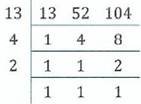
GCF=13 x 1=13

LCM= 13 x 4 x 2 = 104

---

23. Calculate the value of , x + y + 2z ? 12 when x = 5 , y = 8 and z = 9 .

Soln.

Given x=5, y=8 and z=9

Required value of : x + y +2z -12

Now, substitute the given values into the expression above x + y +2z -12 = 5 + 8 + 2(9) - 12

=13 +18 - 12

=19

Therefore, x + y +2z -12 =19

---

24. Find the product of the G.C.F and L.C.M of 4, 8 and 12.

Soln.

G.C.F =2 x 2 =4

L.C.M =2 x 2 x 2 x3 =24

Product of GCF and LCM =4 x 24 =96

---

25. Calculate the sum of the prime numbers between 70 and 90.

Soln.

List of prime numbers between 70 and 90 are 71, 73, 79, 83 and 89

Their sum = 71 +73+79+83 +89 =395

---

26. Find the Greatest Common Factor (GCF) of 18, 24 and 60. 1(a) GCF of 18, 24 and 60

soln.

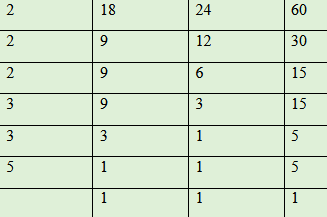
GCF = 2×3 =6

---

27. Mangoes are to be exactly divided into groups of 20, 30 or 36 .What is the minimum number of mangoes required?

Soln

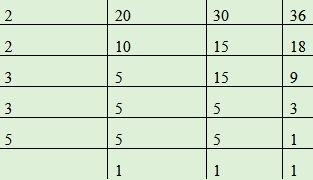
To get the minimum number of mangos, you have to find th LOWEST COMMON MULTIPLE of 20, 30 and 36

LCM=2 x 2 x 3 x 3 x 5

LCM=180.

Therefore, the minimum number of mangoes required is=180