PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM FOUR
MID-TERM-AUG/SEPT – 2024
TIME: 3HOURS
INSTRUCTION
- This paper consists of two sections A and B with total of fourteen (14) questions
- Answer all questions
- Programmable calculators, phones and any other unauthorized materials are not allowed in examination room
- Write your examination on every page of your answer sheet provided
- All diagrams must be drawn in pencils
- All writings must be in black/blue ink
SECTION A. 60 MARKS
1. (a) Three brothers visit the grandfather at intervals of 5days, 7 days and 12 days. If they start together at 15th July. Then find the date that they will visit the grandmother together next time. (Each moths are 30 days)
(b) The total mass of cotton harvested in Ali’s district was 17452.225 kg. Round off this number to the nearest (i) Hundreds (ii) Thousandth.
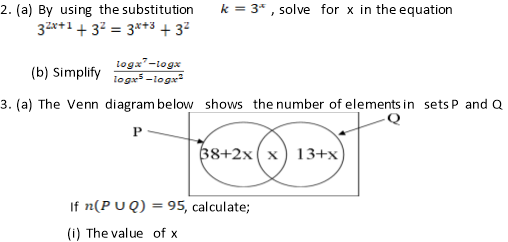
(ii) ![]()
(b) A letter is chosen from the word “RANDOM”. What is the probability that it is;
(i) n? (ii) A vowel
- (a) Find the equation of the line which is parallel to the line x +4y -1 = 0 and which passes through the point (4, -3)
-
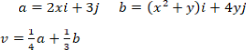 If and
If and 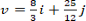 Find x and y given that
Find x and y given that
-
- In the following figure, a regular hexagon is inscribed in a circle.
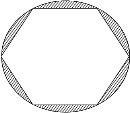
If the perimeter of the hexagon is 42cm. find
(i) the radius of the circle
(ii) the radius of the circle
(iii) the area of the circle and the regular polygon
- (a) In the preparation of Pepsi cola, a bottling filling machine can fill 1,500 bottles in 45
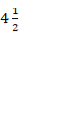 minutes. How many bottles will it fill in hours?
minutes. How many bottles will it fill in hours?
- The energy (E) stored in an elastic band varies as the square of the extension (x). When
the elastic band is extended by 4cm; the energy is 240Joules. What is the energy stored when the extension is 6cm? What is the extension when the stored energy is 60 Joules?
- (a) A car which its buying price was sh.12, 500,000 was sold at a loss of 40 percent. Find the loss made and selling price
- Given the following transactions
Sales for 2009. ......................................................................... 51,000/=
Stock at start. ............................................................................. 9,000/=
Purchases. ................................................................................. 34,650/=
Stock at close .............................................................................. 6,000/=
Returns on sales (inwards). .......................................................... 1,000/=
Return outwards (return on purchase). ............................................. 150/=
From the above transactions, deduce
(i) Cost of sales
(ii) Average stock
(iii) Rate of stock turn
(iv) Net sales (turnover)
- (a) How many integers are there between 14 and 1,000 which are divisible by 17?
(b) The 4th and 7th terms of a G.P are 144 and 18 respectively. Find
- The common ratio
- The first term
- The sum of the first six terms
- (a) A ladder reaches the top of wall 18m high where the other end on the ground is 8m from The wall. Find the length of the ladder,
(b)Verify that
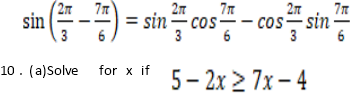
(b). The length of the sides of a right angled triangle is (2x+1) cm, (2x1) cm and xcm. Find x if 2x+1 is the hypotenuse
SECTION B (40 marks)
- (a) The following table shows the distribution of marks scored by 42 candidates in Mathematics exam at Kihesa Secondary School of Mock 2023.
| Marks (%) | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 |
| frequency | 7 | x | 11 | y | 4 | 2 |
Calculate
- The values of x and yif the Mode and the modal class is 53.75 and 50-55 respectively.
- The mean (use an assumed mean of the class mark within the modal class)
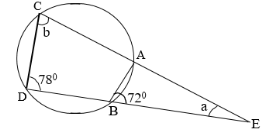
(b) Find the value of angles a and b in the figure below
![]()
![]()
![]()
- (a) The following rectangular prism represents a room 6m by 5m by 4m.
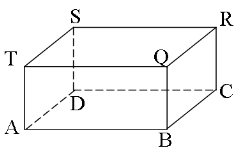
(i) Calculate the diagonal AR
(ii)Find the angle AR makes with the floor (iii) Find the total surface area
- Find the distance (in km) between towns P (12.450S, 30.50E) and Q (12.40S, 39.90E) along a line of latitude, correctly to 4 decimal places.
- (a) Find the value of k such that the matrix is singular 4
![]()
- The vertices of triangle ABC are A (1,2) B (3,1) and C (-2,1). If the triangle is reflected in the x –axis. Find the coordinates of the vertices of its image.
- Solve the following simultaneous equations by matrix method
![]()
-9x+8y – 1 = 0
- (a) A technical school is planning to buy two types of machines. A lather machine needs 3m2 of floor and a drill machine requires 2m2. The total space available is 30m2. The cost of one lather machine is 25,000 shillings, a drill machine costs 30,000 shillings and the school can spend not more than 300,000. Find the greatest number of machines the school can buy. (b) Given that
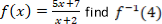
FORM FOUR MATHEMATICS EXAM SERIES 199
FORM FOUR MATHEMATICS EXAM SERIES 199
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
MID TERM EXAMINATION AUG- 2023
SECONDARY EXAMINATION SERIES
MATHEMATICS FORM FOUR
TIME: 3 HOURS AUG-2023
Instructions
- This paper consists of section A and B with fourteen (14) questions.
- Answer all questions.
- Each question in section A caries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- Mathematical tables and non – programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room
- Write your Examination number on every page of your answer booklet(s).
SECTION A (60 MARKS)
- (a) Simplify the sum of 85% of 9861 and
 of 12458. Write your answer correct to two significant figures.
of 12458. Write your answer correct to two significant figures.
(b) (i) Mr. Tumai Distributed Tshs 960,000/= awards to students who passed well in their examinations and their respective teachers as follow: 23% to all students who passed Arts Subjects. 15% to students who passed Mathematics and 27% to students who passed science subjects. The remained amount was distributed to teachers. Find the amount that were awarded to teachers.
(ii) Three bells commence tolling together and toll at intervals of 8, 10 and 12 seconds respectively. How many times do they toll together in 50 minutes?
- (a) If
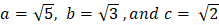 . Simplify
. Simplify 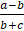
(b) Describe the applications of Logarithm in real life situations
- In a certain class MSUVA displayed counting numbers less than 30. From the displayed numbers, OKWI mentioned all numbers divisible by 2 and FEITOTO mentioned all numbers that were the multiples of 3.
- (i) Outline all numbers that were mentioned by OKWI and FEITOTO in common.
(ii) How many numbers were mentioned by either OKWI or FEITOTO?
- If a number was selected at random from the numbers displayed by MSUVA, what is the probability that a selected number was a multiple of 3?
- (a) Given that
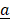 = 4i + 3j and
= 4i + 3j and 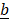 = 6i – 3j, find the value of “h” and “k” if h
= 6i – 3j, find the value of “h” and “k” if h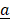 + k
+ k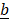 = 10i + j
= 10i + j
(b) A perpendicular line from the point P(2,-4) to the line meets the line at point Z(-1,3). Find:
i. Distance ![]()
ii. If the point Z(-1,3) is a mid-point of the line ![]() , find the coordinates of point
, find the coordinates of point ![]()
- (a) In the following figure;
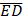 //
//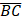 and
and 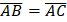 ; If
; If 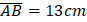 and
and 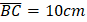 , find the Area of BCDE
, find the Area of BCDE
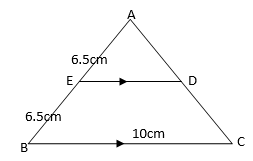
(b) By considering the Alternating opposite angles theorem, draw the diagram hence identify the corresponding angles.
- (a) The time “t” taken to buy fuel at LAKE OIL PETROL STATION in Morogoro varies directly as the number of vehicle “V” in the queue and inversely as the number of pumps “P” available in the station. In petrol station with 10 pumps it takes 20 minutes to fuel 40 vehicles.
- Write vehicle “V” in terms of pumps “P” and time “t”
- Find the time it will take to fuel 60 vehicles in a station with 4 pumps.
(b) Mayele bought 3 bottles of juice of capacity 350 ml and Dialo bought 1 bottle of juice of capacity 1 litre.
i. Who had more juice to drink?
ii. How much more?
- (a) What do the following terms mean as used in Accounts?
- Cash book
- Assets
- Credit transactions
(b) A company bought two cars for Tshs 25,000,000/= each. If one car was sold at a profit of 18% and another was sold at a loss of 6%. In the whole transactions there were no loss. What was the profit made by a company?
- (a) A BODA BODA driver rates after each kilometre. The fare is Tshs. 1000/= for the first kilometre and raise by Tshs. 500/= for each additional kilometre. If BALEKE want to travel 10 kilometres by BODA BODA. What will he be charged by BODA BODA driver?
(b) The number 19683 is in which term in the following Geometric sequence; 3, 9, 27 …?
- (a) If the square of the hypotenuse of an isosceles right-angled triangle is 128 cm2 find
the length of each other sides
(b) From the top of a tower of height 60m the angles of depression of the top and the bottom of a building are observed to be 300 and 600 respectively. Find the height of the building.
- (a) If the length of each side of a square is increased by 6, the area become increased to 16 times the area of the small square. Find the length of one side of the original square.
(b) A large rectangular garden in a park is 120m wide and 150m long. A contractor is called in to add a brick walkway to surround this garden by the same width. If the area of the walkway is 2800m2, how wide is the walkway?
SECTION B (40 MARKS)
- (a) In certain research the data were summarized as shown in a table below:
| Class Mark | 10 | 15 | 20 | 25 | 30 | 35 |
| Frequency | 3 | 2 | 10 | 5 | 4 | 1 |
By using the data above reconstruct a frequency distribution table including class interval and frequency.
(b) Prove that equal chords of a circle subtend equal angles at a centre.
- (a) Two towns P and Q on the Latitude 480 are 370 Nautical miles apart. Find the
difference in their longitude.
(b) A pyramid with vertex V and edges VA, VB, VC, VD each 15cm long has a rectangular base ABCD where AB = CD = 10cm and AD = BC = 8cm.
i. Sketch the pyramid using the above information.
ii. Calculate the height “VO” of the pyramid where “O” is the centre of the rectangle.
- Calculate the angle between the base and edge
- (a). (i). Find the possible values of x if the matrix
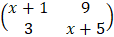 has no inverse.
has no inverse.
(ii). By using matrix method, solve the equations ![]()
(b). A transformation is given ![]()
![]() and
and ![]() , find the image of the equation 2x – 3y = 6 under the transformation matrix which performs the above transformations.
, find the image of the equation 2x – 3y = 6 under the transformation matrix which performs the above transformations.
- (a) A function f is defined as;
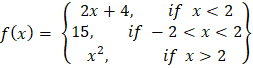
Find (i) f(1.95) (ii) f(15) (iii) Domain of f (iv) identify the type of a function f
(b) A school is preparing a trip for 400 students. The company who is proving the
transportation has 10 buses of 50 seats each and 8 buses of 40 seats, but only 9 drivers available. The rental cost for a large bus is 800,000/= and 600,000/= for the small bus. How many buses of each type should be used for the trip for the least possible cost?
Page 1 of 6
FORM FOUR MATHEMATICS EXAM SERIES 172
FORM FOUR MATHEMATICS EXAM SERIES 172
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCY BASED SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS
FORM FOUR- SEPT 2022
INSTRUCTION
- This papers consist of sections A and B with a total of fourteen (14) questions
- Answer all questions
- Each question A carries six (06) marks while each question in section B carries ten (10) marks
- All necessary working and answers for each question must be shown clearly
- Mathematical table and non-programmable calculators may be used
- All communication devices and any unauthorized materials are NOT allowed in the examination room
- Write your examination number on every page of your answer booklet(s)
SECTION A: (60 MARKS)
Answer all questions in this section
- (a)Round each of the numbers x=2.354, y=4.843 and z=1.789 to one decimal place and then use the results obtained to find the value of A to two significant figures given that
![]()
![]() If k=0.5
If k=0.5![]() and P=0.8
and P=0.8![]() , find the value of
, find the value of ![]()
- (a)Use the substitution = 2y to solve the equation 22+1 – 2y+2 + =2y
(b)Find the solution set of the system
![]()
- (a)In a class of 40 students, each must take at least one of the subject either mathematics or Additional mathematics. If 25 students take mathematics and 20 Additional mathematics,
Determine
- The number of those who take both subjects
- The number of those who take mathematics but not Additional mathematics
(b)(i) What do the mutually exclusive events mean as used in probability?
(ii))Find the probability of obtaining a 3 or 5 in one roll of a die
- (a)Given two lines 5x + 6y=5 and kx – 3y=10, find the value of k if the lines are;
- Perpendicular
- Parallel
(b)Given vectors ![]() calculate,
calculate,
(i) ![]() (ii) |w|w
(ii) |w|w
- (a)Two triangles are similar. The ratio of their corresponding sides is 4:5. If the area of the first triangle is 20cm2, find the area of the second triangle.
(b)The interior angle of regular polygon is 120° greater than the exterior angle. Find the number of sides of the polygon and hence identify the name of the polygon.
- (a)Mr. Haruna bought a car from Japan worth 5,900,000 Japanese Yen. When he arrived in Tanzania he was charged custom duty of 25% on the car. If the exchange rate were as follows
1 us dollar = 118 Japanese Yen
1 us dollar = 76 Tanzanian shillings
Calculate the total cost of buying a car including the charged custom duty of 25% in Tanzania shillings.
(b) The number of eggs which a goose lays in a week varies as the cube root of the average number of hours of sleep she has. When she has 8 hours sleep, she lays 4 eggs. How long does she sleep when she lays 5 eggs?
- (a)Moses sold his computer for sh. 2,430,000 and result lost 20% of the price he paid for it.
- How much did he pay for the computer/
- What was the loss he incurred
(b)(i)The ratio of boy to girls at Mtakuja secondary school is 3:7. If the school has 500 students, find the number of boys at the school.
(ii)Define the term trial balance as used in Accounts and write one uses of it.
- The third, the fourth and eight terms of arithmetic progression (A.P), forms the first three consecutive terms of a geometric progression (G.P). If the sum of the first ten terms of the A.P is 85. Calculate
- The first terms of both the A.P and the G.P
- The common ratio
- The sum of the first 5 terms of the GP
- (a) Given that
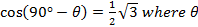 is an acute angle, without using tables, find the value of
is an acute angle, without using tables, find the value of 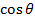
(b)A building has an angle of elevation of 35° from point P, and angle of the elevation of 45°from a point Q. if the distance between points P and Q is 30cm, what is the height of the building (Write your final answer to the nearest whole number)
- (a)Solve for if
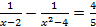
(b)Find two consecutive numbers such that the sum of their squares is equal to 145.
SECTION B: (40 Marks)
Answer all questions in this section
- (a)The examination score of 33 students are given on the following cumulative frequency table.
| Class interval | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Cumulative frequency | 2 | 4 | 9 | 17 | 29 | 33 |
- Find the mean score
- Find the median and median class
- Find the mode and the modal class
(b)Show that the radius of a circle with an arc of a length ![]() m and central angle
m and central angle ![]() is 6m
is 6m
- (a)(i) Calculate the volume of a right cylinder whose base radius is 18cm, and the height is 14cm (Use
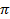 = 3.142) (ii)Calculate the total surface area of a right circular cone below, whose base radius is 5cm and whose height from the vertex to the centre is 12cm. (Use
= 3.142) (ii)Calculate the total surface area of a right circular cone below, whose base radius is 5cm and whose height from the vertex to the centre is 12cm. (Use 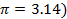
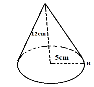
(b)Calculate the distance from Ruvuma (15°S, 45°E) to Mtwara (15°S, 49E) in km. use ![]() and the diameter of the earth as 12800km and the answer should be correct to two decimal places.
and the diameter of the earth as 12800km and the answer should be correct to two decimal places.
- (a)Determine the Matrix A from the equation
![]()
(b)A liner transformation maps the point (x,y) onto (x' y') where x'=4x + 3y and y'=x – 2y. Find
- The matrix T
- Inverse of the matrix T
- The image of a point (5,3) under T
- (a)If f(x) = x2 – 4x+3
Find (i) f-1 (x)
(ii) the domain and range of f(x)
(b)A shopkeeper buys two types of sugar, White sugar and brown Sugar. The white sugar is sold at shs 40,000/= per bag and the brown sugar is sold at shs 60,000/= per bag. He has shs 1,500,000/= available and decides to buy at least 30 bags altogether. He has also decides that at least one third of 30 bags should be brown sugar. He buy x bags of white sugar and y bags of brown sugar.
- Write down three (3) inequalities which will summarize the above information.
- Represent these inequalities graphically
- The shopkeeper makes a profit of shs 10,000/= from a bag of white sugar and shs 20,000/= from a bag of brown sugar. Assuming he can cell his entire stock, how many bags of brown sugar. Assuming he can cell his entire stock, stock, how many bags of each type should he buy to maximize his profit? Find that profit.
FORM FOUR MATHEMATICS EXAM SERIES 120
FORM FOUR MATHEMATICS EXAM SERIES 120
THE UNITED REPUBLIC OF TANZANIA
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM FOUR MID TERM EXAMINATION-2021
041 BASIC MATHEMATICS
Time: 3 Hours AUG, 2021
Instructions
- This paper consists of section A and B with a total of fourteen (14) questions
- Answer all questions in sections A and B, each question in section A carries six (6) marks while each question in section B carries ten (10) marks
- NECTA Mathematical tables may be used
- Cellular phones, calculators and any unauthorized materials are not allowed in the examination room
- Write your examination number on every page of your answer sheet (s)
SECTION A (60 MARKS)
Answer all questions in this section
- (a) Simplify
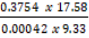 without using mathematical table express your answer in four significant figures.
without using mathematical table express your answer in four significant figures.
(b) Jenk and Jemry are riding on a circular path. Jenk completes a round in 24 minutes where as Jemry completes a round in 36 minutes. If they started at the same place and time and go in the same direction, after how many minutes will they meet again at the starting point?
- (a) Use mathematical table to evaluate
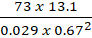
(b) Find the value of x and y if ![]() = 2025
= 2025
- (a) Let U be a universal set and A and B be the subsets of U where
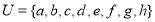 ,
, 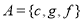 and
and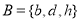 .
.
- Find the number of subsets of set A’
- Find
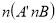
- If an element is picked at random from the universal set (u), find the probability that it is an element of set B
(b) Find the probability that a king appears in drawing single card from an Ordinary deck of 52 cards
- (a) The coordinate of P, Q and R are (2, m), (-3, 1) and (6, n) respectively. If the length of PQ is
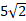 units and midpoint of QR is
units and midpoint of QR is 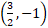 find the possible value of m and n
find the possible value of m and n
(b)The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
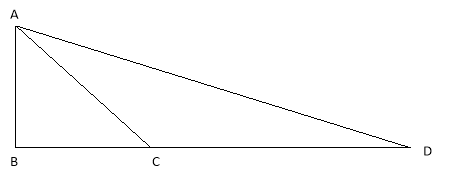 (a) if
(a) if 
 and angle ABD =
and angle ABD = 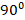 Calculate the length
Calculate the length 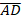
(b) (i) Given ![]() =
= ![]() =
= ![]() = 3 where
= 3 where ![]() ,
,![]() and
and ![]() are the sides of the triangle ABT and
are the sides of the triangle ABT and ![]() ,
,![]() and
and ![]() are the sides of the triangle KLC. What does this Information imply?
are the sides of the triangle KLC. What does this Information imply?
(ii) A regular Hexagon is inscribed in a circle if the perimeter of the hexagon Is 42cm, find the radius of the circle and its Area
- (a) If y varies inversely as
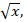 and x is multiplied by n. What is the ratio of the first y to the second y?
and x is multiplied by n. What is the ratio of the first y to the second y?
(b) The headmaster has enough food to last for his 600 students for 20 days from tomorrow. If 120 students leave the school today for UMISSETA game, how long will the food last?
- (a) By selling an article at shs 22,500/= a shopkeeper makes loss of 10%. At what price must the shopkeeper sell the article in order to get a profit of 10%?
(b) The following trial balance was extracted from the books of Nzilandodo on 31st December 2005.
TX MARKET LTD
TRIAL BALANCE AS AT 31.12.2005
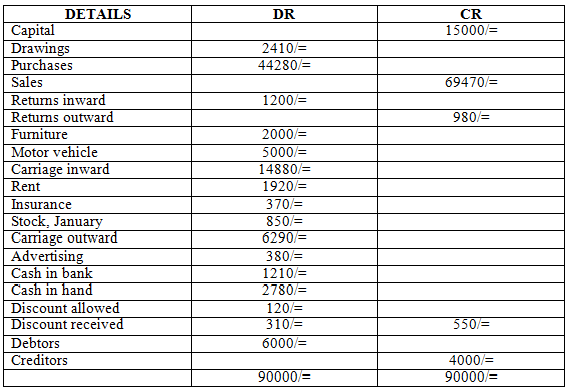
Note: Stock at close 31st December 7360. Required, prepare balance sheet as that date.
- (a) The sum of the first six terms of an A.P is 72 and the second term is seven times the fifth term.
- Find the first term and the common difference
- Find the sum of the first ten terms
(b) Find the sum of the first four terms of a geometric progression which has a first term of 1 and a common ratio of ![]()
- (a) If tan A =
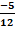 , where A is an obtuse angle,
, where A is an obtuse angle,
Find (i). Cos A + Sin A (ii). – Cos2 A – Sin2 A
(b) A and B are two points on the ground level and both lie west of flagstaff. The angle of elevation of the top of the flagstaff from A is 560 and from B is 430. If B is 28m from the foot of the flagstaff. How far apart are the points A and B?
- (a) Solve the quadratic equation x2 – 8x +7 = 0
(b) A field is 10m longer than its wide. The area is 7,200m2. What is the width?
SECTION B (40 marks)
Answer all questions in this section
- ( a) Consider the following frequency distribution tale below;
| Marks | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 | 100-109 | 110-119 |
| Freq | 1 | 2 | 5 | 11 | 21 | 20 | 17 | 10 | 6 | 4 | 2 | 1 |
Draw the histogram and use it to estimate the mode in one decimal place.
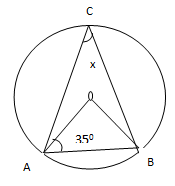
b) Find the value of angle X in the figure below.
- (a) A rectangular box with top WXYZ and base ABCD has AB=9cm, BC=12cm and WA = 3cm

Calculate (i) The length AC (ii) The angle between WC and AC
(b) Two places P and Q both on the parallel of latitude ![]() N differ in longitudes
N differ in longitudes
by ![]() find the distance between them along their parallel of latitude.
find the distance between them along their parallel of latitude.
- (a) If matrix A is singular, what will be the value of y given that
![]()
(b) Solve the following simultaneous equation by matrix method
2x + y = 7
4x+3y = 17
(c) Find the image of (3, 5) after rotation of 270o about the origin in anticlockwise direction.
- (a) If f(x) is the function such that
f(x)=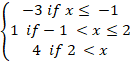
- Sketch the graph of f(x)
- State the domain and range of f(x)
(b) A transport company is hired to transport 420 people it has two types, P and Q of vehicle to be used. Type P carries 35 passengers and type Q carries 14 passengers. There are at least 10 vehicles of type Q and not more than 9 vehicles of type P. Write down inequalities to represent this information.
1 of 5
FORM FOUR MATHEMATICS EXAM SERIES 64
FORM FOUR MATHEMATICS EXAM SERIES 64
THE PRESIDENT'S OFFICE
MINISTRY OF REGIONAL GOVERNMENT AND LOCAL GOVERNMENT
PRE-NATIONAL EXAMINATION SERIES-1
MATHEMATICS FORM-4
2020
TIME: 3:00 HRS
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in sections A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) Mangoes are to be exactly divided into groups of 20, 30 or 36 .What is the minimum number of mangoes required?
(b) Mary was given 60,000 shillings by her mother. She spent 35 percent of the money to buy shoes and 10 percent of the remaining money to buy books. How much money remained?
2. (a). Evaluate log10 40,500 given that log10 2 = 0.3010 , log10 3 = 0.4771 and log10 5 = 0.6990.
(b). Find the values of x and y if
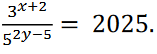
3(a) Factorize the following expressions:
(i) 16y2 +xy -15x2
(ii) 4 - (3x - 1)2
(b) At Moiva’s graduation ceremony 45 people drank Pepsi-Cola, 80 drank Coca-Cola and 35 drank both Pepsi-Cola and Coca-Cola. By using a Venn diagram, found out how many people were at the ceremony if each person drank Pepsi-Cola or Coca-Cola.
4. (a) Given vectors a = 6i + 12j, b = 17i + 18j :
(i) Find the vector c = 2a – b and its magnitude correctly to 3 significant figures. (ii) Represent vector c in part (a)(i) on the x - y plane.
(b) Find the equation of the line passing passing through the midpoint of the points A(− 3 2, ) and B(1,− )4 and which is perpendicular to line AB .
5. (a) In triangle ABC , X , Y and Z are the midpoints of sides AB , AC and BC respectively. If
ZX = ZY and ZXBˆ = ZY Cˆ = 90°;
(i) Represent this information diagrammatically, (ii) Show that ABZˆ = ACZˆ .
(b) The areas of two similar polygons are 27 and 48 square metres. If the length of one side of the smaller polygon is 4.5 cm, find the length of the corresponding side of the larger polygon.
6. (a) The variable v varies directly as the square of x and inversely as y. Find v when x = 5 and y = 2 ? given that when v = 18 and x = 3 the value of y = 4 .
(b) The temperature (Ti) inside a house is directly proportional to the temperature (To) outside the house and is inversely proportional to the thickness (t) of the house wall. If Ti = 32°C when To = 24°C and t = 9cm , find the value of t when Ti = 36°C and To = 18°C
7.(a)Given that 49, x and 81 are consecutive terms of a geometric progression. Find:
(i) The value of x.
(ii)The geometric mean.
(b) A wall is in the shape of a trapezium. The first level of wall is made-up of 50 bricks where as the top level has 14 bricks. If the levels differ from each other by 4 bricks, determine the number of
(i) levels of the bricks.
(ii) bricks used to make the wall.
8. (a) Three relatives shared Tshs 140,000 so that the first one got twice as much as the second, and the second got twice as much as the third. How much money did the first relative get?
(b) Kitwana paid Tshs 900,000 for a desktop computer and sold it the following year for Tshs 720,000. Find:
- The loss made,
- The percentage loss.
10. (a) Solve the equation 4x2 ? 32x + 12 = 0 by using the quadratic formula.
(b) Anna is 6 years younger than her brother Jerry. If the product of their ages is 135, find how old is Anna and Jerry.
9. (a) A river with parallel banks is 20 m wide. If P and Q are two points on either side of the river, as shown in the figure below, find the distance PQ.

(b) In the triangle LMN , LM = 5m, LN = 6m and angle MLN = 66°. Find MN .
SECTION B (40 Marks)
Answer four (4) questions from this section.
11. A shopkeeper sells refrigerators and washing machines. Each refrigerator takes up 1.8 m 2 of space and costs 500,000 2 of space and costs 300,000 shillings; whereas each washing machine takes up 1.5 mshillings. The owner of the shop has 6,000,000 shillings to spend and has 27 m 2 of space.
(a) Write down all the inequalities which represent the given information.
(b) If he makes a profit of 30,000 shillings on each refrigerator and 40,000 shillings on each washing machine, find how many refrigerators and washing machines he should sell for maximum profit.
12. (a) Given:
Opening stock 01-01-2012 34,430/=
Closing stock 31-12-2012 26,720/=
Net purchases during 2012 212,290/=
Expenses for the year 45,880/=
Gross Profit is 50% of cost of goods sold
Find: (i) Cost of goods sold (ii) The gross profit
(b) On 1 st June, 2013 Mrs. Lemisha started business with capital of 100,000/= and mad ehte following transactions
June 2 bought furniture 40,000/=
7 bought goods 70,000/=
11 sold goods 65,000/=
16 paid Sundry expenses 30,000/=
19 cash sales 80,000/=
24 paid wages 50,000/=
26 withdraw cash 30,000/=
(i) Prepare the cash account
(ii) Prepare the balance sheet as at 30/06/2013
(iii) Explain the importance of the balance sheet you have prepared in part (b)(ii) above.
13.(a) Given matrices
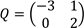
And
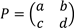
Such that
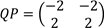
Find elements of matrix P
(b) Determine the matix A from the equation
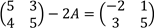
14.(a) A ship sails from Pemba (4.5°S, 39.5°E) to Dar es salaam (7.5°S, 39.5°E). If it leaves Pemba at 11:30 am and arrived in Dar es salaam at 13:30 pm, use 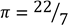 and RE=6370km to find speed of ship in km/h
and RE=6370km to find speed of ship in km/h
(b) Sketch a square pyramid whose base is PQRS, vertex is at W and centre is at N, then answer the questions that follow:
(i) State the projection of 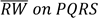
(ii) Name the angles between 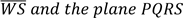
(c) The volume of a square pyramid is 28.2 cm3. If the sides of its base are 4 cm long, find the height of the pyramid correct to one decimal place.
FORM FOUR MATHEMATICS EXAM SERIES 28
FORM FOUR MATHEMATICS EXAM SERIES 28
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256