PRESIDENT’S OFFICE
REGIONAL, ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM THREE MID TERM EXAMINATION
041 BASIC MATHEMATICS
TIME:3 HOURS AUG, 2023
INSTRUCTION
1. This paper consist of two sections A and B
2. Answer all questions
3. Calculators and mathematical tables may be used
4. All diagram must be drawn by using pencil![]()
5. All writing must be in a blue or black ink
SECTION A (60 MARKS)
1. (a) If a=![]() write in the form of a/b where b≠0
write in the form of a/b where b≠0
(b)Three bells are set to ring at intervals of 12 minutes,15 minutes and 24 minutes. If they started together at 2:00 pm, then find at what time will the bells ring together for second time
2. (a)Find the value of X if (![]() )x+3(
)x+3(![]() )-x=1
)-x=1
(b)Solve for X if log39-1=X2-2x-5
3. (a)If ![]() = p+q√r, simplify by rationalizing the denominator and hence find the value of p, q and r
= p+q√r, simplify by rationalizing the denominator and hence find the value of p, q and r
(b)In a class of 100 students, 38 study mathematics,20 study biology and 45 study neither of two subjects by using venn diagram, find the number of students who
(i)Study both subjects
(ii)Study exactly one subject
4. (a) A straight line has a gradient of ![]() and it passes through the point (-1,2). Find
and it passes through the point (-1,2). Find
(i)Its equation
(ii)The Y-intercept
(b)Make V the subject from ![]()
![]() =
= ![]()
5. (a) a radio is bought for sh.24,000 a sold for sh. 36,000. Find the
- The profit made
- The percentage profits
(b) The operation a![]() b = (a+b)2- ab
b = (a+b)2- ab
Find the value
- 3
 2
2 - 9
 -
-
6. (a) The variable V varies directly as the square of X and inversely as Y. Find V when X =5 and Y=2, When V =18, X=3 and Y =4.
(b) Water from a tap gets into a tank at a rate of 20 litres per minutes. How long will it take to fill a tank that is 10,000 litres. Give your answer in hours and minutes.
7. (a) Find the first term and common difference of an arithmetic progression whose 5th term is 21 and 8th term is 30.
(b) The products of three terms of a geometric progression (GP) is 8000. If the first term is 4. Find the second term and the third term.
8. (a) How many grams are there 0.00912 tones?
(b) A ladder 15cm long leans against of vertical wall so that angles make with the horizontal ground is two times that makes vertical wall. Calculate how far up the wall does the ladder reaches?
9. (a) Basil has to share eighty books with his daughters Rose and Nancy. He decided that for every two books Nancy gets, Rose gets three books and he gets five books. Find the number of books each gets.
(b) Solve by elimination method 2x – y = 1
x + y = 1
10. (a) Solve the quadratic equation x2-8x+7=0 by completing the square
(b) A field is 10m longer than its wide. The area is 7200m2. What is the width?
SECTION B (40 MARKS)
11. The table below represents score of 100 students in geography test
| Marks ( | 40 - 49 | 50 - 59 | 60 - 69 | 70 - 79 | 80 - 89 | 90 – 99 |
| Frequency | 7 | 13 | 36 | 30 | X | 4 |
- Determine the value of X
(b) By using assumed A=74.5, determine mean
(c) Find mode
(d) Find median
12. (a) Kwembe went to the market with 3000Tsh to buy oranges and mangoes. He bought 20 oranges and 5 mangoes. If Grace went to the same market with 2000Tsh and bought 10 oranges and 5 mangoes. What is the price of one mango and one orange?
(b) Mchilo invested a certain amount of money in a saving Bank whose interest rate was 10![]() compound annually. After two years he got 5000 shillings.
compound annually. After two years he got 5000 shillings.
(i) How much did he invest at the start?
(ii) How much did he receive as interest at the end of two years?
13. (a) Given a function f(x)=x2-2x-3. Find
(i) Line of symmetry
(ii) The turning point
(iii) Express f(x) in the form of a(x+b)2+c where a,b and c are real numbers
(b) If f(x) is the function such that
F(x)=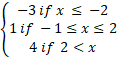
(i) Sketch the graph of f(x)
(ii) State the domain and range of f(x)
(iii) Find the value of f(100)
14. MRS CHENI started a business on 16thMarch 2023 with capital in cash 2,066,000
March 17 Bought goods for cash 1,000,00/-
19 Bought shelves for cash 110,000/-
20 Sold goods for cash 900,000/-
21 Purchased goods for cash 800,000/-
22 Sold goods for cash 1,400,000/-
26 Paid rent 300,000/-
(i) Record the above transaction in cash account
(ii) Extract a trial balance
1
FORM THREE MATHEMATICS EXAM SERIES 147
FORM THREE MATHEMATICS EXAM SERIES 147
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT AUTHORITY
BASIC MATHEMATICS EXAMINATIONS- AUG 2021
FORM THREE
TIME: 3:00HRS
INSTRUCTIONS
- This paper consists of Sections A and II
- Answer ALL questions in both sections
- Mathematical table and graph paper may be used unless otherwise stated.
- Write your Examination Number on every page of your answer sheet(s) provided.
SECTION A (60MARKS)
- (a) A school trip of 32 people went to a tour which costs a transport fee of 580/= each person. What was the approximate total transport cost?
b) Rajabu is making some small metal rods.He has three peaces of metals of length 432cm, 648cm,540cm.What is the largest length of a rod he can make if the rods have the same length and no metal is wasted.
- (a) Without using mathematical table simplify √63+√72
√32+√28
(b)Find the value of x in log( - 1) + 2 = log(3 + 2) + log 25
- a)(i) List all the subsets of the following set A = {3, 6, 8}
( ii) Work out the number of subsets in a set containing 6 elements.
b) In a class of 45 students, 19 study commerce but not physics, 16 study physics but not commerce and 3 studies neither commerce nor physics, find the number of students who study (i) Physics or commerce (ii) Both subjects
- (a) The line joining (2,-3) and (k,5) has a gradient -2, find k
b) ?PQR is such that PQPR and PQ:QR is equal to 3:4.If the perimeter of the triangle is 60cm. Calculate the value of QR.
- (a) Calculate to 1 decimal place the area of an equilateral triangle of side 10cm.
(b) In the figure below find MK and MP
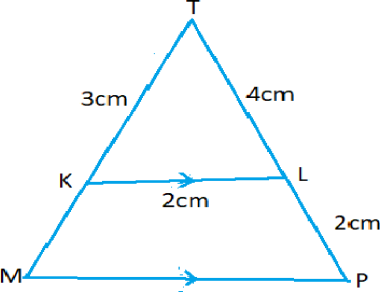
- (a) A man is paid 6000/= for 8 hours work (i) What is his rate of pay? (ii) At this rate how long must he work to receive 30,000/=
b) In working for 10 hours a day, 12 men can do a certain piece of work in 6 days. For how many hours a day must 20 men work in order to do the same amount of work in 14 days?
- a) By selling an article at Tsh 225,000 shopkeeper makes a loss of 10%.At what price must the shopkeeper sell the article in order to get a profit of 10%?
b) Find the total amount of money received if Tsh 800,000 is deposited in a bank at the rate of 9% compounded semi anually in one year.
| ~ =, | L is a mid point of KM .Prove that L ≡ L |
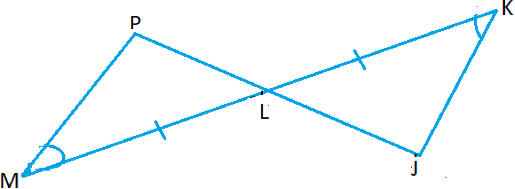
(b) Given the angles A? C = 2x+30° and C? D = (x+15)°. If two angles are complementary find the value of x and the size of each angle
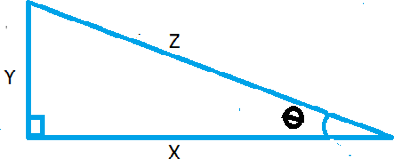
- (a) Given the right angled triangle below with sides marked x , y , z ,
Prove that cos2 + sin2=1
b) A pole 7.45m high casts a Shadow 4.05m long on horizontal ground. Find the angle of elevation of the sun.
10. (a) Expand the expression (ax + c) (bx – d)
(b) A boy bought some packets of biscuits for 120/=.If the biscuits had been 3/= a packet cheaper he would have received 2 more packets for his money. How many packets did he buy?
SECTION B (40MARKS)
11. In a mathematics Examination the following marks were obtained:
27 57 57 40 70 48 59 60 42 44 47 44 44 59 35 48 43 52 36 48 Group the marks in class interval of 20-29, 30 -39 , . . . Then
- Construct the frequency distribution table
- Calculate the mean marks by using assumed mean method (Take A =44.5)
- Calculate the mode
- Draw the cumulative frequency curve then estimate the median
12. (a)Four positive numbers are consecutive elements of geometric progression (G.P).The product of the first and the third number is 36 while the product of the second and fourth number is 324. Find the sum of nine terms of the G.P
(b) The second , fourth and eighth terms of an Arithmetic Progression form a Geometric progression and the sum of the third and fifth terms of AP is 20. Find the first four terms of the geometric progression.
13. (a) A function is defined as f(x ) = √4 - 2 find (i) Domain and Range of f(x) (b) Sketch the graph of function f(x)= { + 3 ? < 1
2 ? > 1
Hence (i) state its domain and range (ii) Find f(6) , f(-2) (iii) State whether the graph is one to one function ?
14. The relation is defined as R={(, ): ≥ —4, 3 - 4 ≤ 12 5 + 4 ≤ 20}
- Draw the graph of R
- State the domain and range of R
FORM THREE MATHEMATICS EXAM SERIES 64
FORM THREE MATHEMATICS EXAM SERIES 64
THE PRESIDENT'S OFFICE
MINISTRY OF REGIONAL GOVERNMENT AND LOCAL GOVERNMENT
AUGUST-SEPTEMBER EXAMINATION SERIES
MATHS FORM-3
2020
TIME: 2:30 HRS
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in sections A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a) If 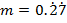 and
and 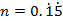 find the fraction of
find the fraction of ![]() in its simplest form
in its simplest form
(b).Find the GCF of 210, 357 and 252.
2.(a)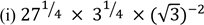
(ii) log3 10 + log3 8.1
(b) If nlog5125 = log264 , find the value of n.
3. (a) By substituting a = 1x and b = 1y in the system of equations:
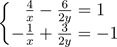 , find the solution set (x,y).
, find the solution set (x,y).
(b) Let U be a universal set and A and B be the subsets of U where:
U = {1,2,3,4,5,6,7,8,9,10}, A = {odd numbers} and B = {prime numbers} (i) Represent this information in a venn diagram.
(ii) Find A ? B′ and (A ? B) ′
4. (a) Given vectors (i) the vector a = 3i + 2 j , b = 8i + 3j and c = 2i + 4 j find:
(i) d=3a -b +1/2c
(ii) a unit vector in the direction of d.
(b) Find the equation of the line passing at point (6, 2) and it is perpendicular to the line that crosses the x-axis at 3 and the y-axis at 4.
5. (a) Two triangles are similar. A side of one triangle is 10 cm long while the length of the corresponding side of the other triangle is 18 cm. If the given sides are the bases of the triangles and the area of the smaller triangle is 40 cm2 , find the area and the height of the larger triangle.
(b) In the figure below CB = BD = DA and angle ACD = x .
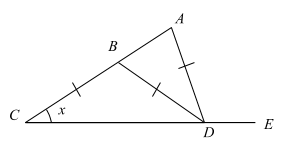
(i) Show that angle ADE = 3x ,
(ii) Calculate the measure of angle CDA if x = 39°.
6. (a) A shopkeeper makes a 20% profit by selling a radio for sh. 480,000.
(i) Find the ratio of the buying price to the selling price.
(ii) If the radio would be sold at 360,000, what would be the percentage loss?
(b) A farmer sold a quarter of his maize harvest and gave one third of the remaining to his relatives. If the farmer remained with 25 bags of maize find how many bags of maize did the farmer harvest.
7. (a) Mariam, Selina and Moses contributed 800,000, 1,200,000 and 850,000 shillings respectively while starting their business.
(i) Find the ratio of their contributions in simplest form.
(ii) If the business made a profit of 1,900,000 shillings; find how much each got if the profit was shared in the same ratio as their contributions.
(b) A dealer bought 10 books for 200,000. He sold 25 of them at 30,000 shillings each and the remaining at 25,000 shillings each. What was his percentage profit?
8. (a) The number of tablets given to a patient was found to be directly proportional to the weight of the patient. If a patient with 36 kg was given 9 tablets, find how many tablets would be given to a patient whose weight is 48 kg.
(b) Four people can eat 2 bags of rice each weighing 10 kg in 12 days. How many people can eat 6 bags of rice of the same weight in 18 days?
9. (a) If the sum of n terms of a geometric progression with first term 1 and common ratio ![]() is
is ![]() , find the number of terms.
, find the number of terms.
(b) How many integers are there between 14 and 1,000 which are divisible by 17?
10.(a) Use factorization method to solve the quadratic equation x2 ? 9x + 14 = 0.
(b) Find the values of x that satisfies the equation
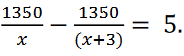
SECTION B( 40 Marks)
Answer All Questions
11.(a) A ship sails from Pemba (4.5°S, 39.5°E) to Dar es salaam (7.5°S, 39.5°E). If it leaves Pemba at 11:30 am and arrived in Dar es salaam at 13:30 pm, use  and RE=6370km to find speed of ship in km/h
and RE=6370km to find speed of ship in km/h
11.(b) Calculate the values of 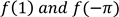 if f is defined as
if f is defined as
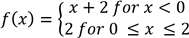
12.Mwanne commenced business on 1st April, 2015 with capital in cash 200,000/=
April 2 bought goods for cash 100,000/=
3 bought goods for cash 300,000/=
4 purchased shelves for cash 230,000/=
5 sold goods for cash 400,000/=
9 paid wages for cash 50,000/=
12 purchased goods for cash 70,000/=
13 sold goods for cash 600,000/=
16 paid rent for cash 100,000/=
20 bought goods for cash 60,000/=
25 sold goods for cash 300,000/=
27 paid salary for cash 70,000/=
Prepare the following:
(a) Cash account, (b) Trial balance.
13. The heights of 50 plants recorded by a certain researcher are given below:
56 82 70 69 72 37 28 96 52 88 41 42 50 40 51 56 48 79 29 30 66 90
99 49 77 66 61 64 97 84 72 43 73 76
76 22 46 49 48 53 98 45 87 88 27 48
54 79 80 73
(a) Copy and complete this tally table for the data given above.
| Height (cm) | Tally | Frequency |
| 21-30 | ||
| 31-40 | ||
| 41-50 | ||
| 51-60 | ||
| 61-70 | ||
| 71-80 | ||
| 81-90 | ||
| 91-100 |
Use this table to:
(b) Draw a histogram for the height of the plants.
(c) Find the mean height of the plants (do not use the assumed mean method).
(d) Find the median of the heights of the plants.
14. (a) In the figure below, BD is a tangent to the circle having the centre O .
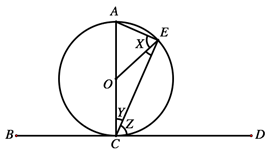
Given that angle OEC = 28°, find the values of angles marked X , Y and Z .
(b) Find the equation of the line passing at point (6, 2) and it is perpendicular to the line that crosses the x-axis at 3 and the y-axis at 4.
FORM THREE MATHEMATICS EXAM SERIES 29
FORM THREE MATHEMATICS EXAM SERIES 29
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256