OFFICE OF THE PRESIDENT, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT,
SECONDARY -EXAMINATION SERIES
MATHEMATICS MARCH EXAMINATION- FORM THREE
Instructions
- This paper will consist of sections A and B with a total of 14 questions
- Answer all questions in both sections A and B
- Section A will carry 60 marks and section B will carry 40 marks
- Mathematical tables/ Calculator may be used
- Write your Examination number on the top right corner of your answer booklet provided. Use R = 6400 and π= 3.14
SECTION A (60 Marks)
Answer all questions in this section
1. a) Mangoes are to be exactly divided into groups of 20, 30 or 36. What is the smallest number of mangoes required?
b) Anna was given 60,000 shillings by her mother she spent 35 percent of the money to buy shoes and 10 percent of the remaining money to buy books. How much money remained?
2. a) If log y + 21og (3x+ l) = l . Express y in terms of x
b) Given a recurring decimal 0.9666666... write it as a fraction.
3. (a) Solve the value of x if
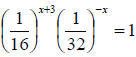
(b) If log 2 = 0.3010, without using mathematical tables, find the value of log 5
4. a) Use the number line to find the value of -3×-4
b) A village received 452009 bags of fertilizer to be distributed to 4500 Farmers. Estimate the number of bags each farmer got?
5. (a) A lecture hall has 20 rows of a seats with 100 seats in the back row, each row have 2 fewer number of seats than the row immediately behind it .How many seats are their in the lecture hall?
(b) Mabrouk invested a certain amount of money in a saving account whose interest rate was 8% compounded annually .After three year ,he got 500,000/=
(i) How much did the invest at the start.
(ii) How much did he received as interest at the end of 3 years?
6. (a) Without using tables, find the value of ![]() and simplify your answer.
and simplify your answer.
(b)The sides of a right angled Triangle are (2x + 1)Cm, (12x)Cm and (12x + 1)Cm. Find the value of x in cm if the hypotenuse is (12x + 1)cm
FORM THREE MATHEMATICS EXAM SERIES 197
FORM THREE MATHEMATICS EXAM SERIES 197
PRESIDENT’S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES,
MID TERM ONE – MARCH-2024
MATHEMATICS FORM THREE
Time: 3Hours
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions in sections A and B
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA Mathematical tables and non-programmable calculator may be used.
6. All communication devices and any unauthorized materials are not allowed in the examination room.
7. Write your examination number on every page of your answer sheet(s).
SECTION A. (40 MARKS)
Answer all questions in this section.
- (a) solve the value of x if
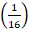 x+3
x+3 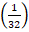 -1 =1
-1 =1
(b) If log 2 =0.0310, without mathematical time table find value of Log 5
- If a = 0.25 and b= 0.5. find the fraction
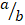 in its simplest form
in its simplest form
(b) Round off (1) 0.002098 to two significant figures
- 7.67 to the nearest whole number
- 2.77 to one decimal place
- (a) how many grams are there in 0.00912 tones
(b) the compression of 1 spring is directly proportional to the thrust T. Exerted on it . if the thrust of 4N produces a compression of 0.8, find
- The compression when the thrust is 5N
- The thrust when the compression is 0.5 cm
- The product of three terms of geometric progression (GP) is 8000. If the first term is 4 , find the second term and third term.
(b)Mahona invested a certain amount of money in serving bank whose interest was 10% compounded annually. After 32 years he got 5000 shillings.
- How much did he invest at the start
- How much did he receive as interest at the end of two years
- (a) Given that log 34 = 1.262 and log 35 =1.1465. find log 30.8
(b) the dimension of first rectangular are length 23cm and width 16 cm. a second rectangle has length 12cm and width 9cm with reasons state wether the two rectangles are similar.
- (a) solve for x in 1≤3x-2<8
(b) By using completing square method, solve equation.
![]() =4
=4
- (a) find the value of Y given that 125y+1+53y=630
(b) find the value of x given that 2log x= log 4+log (2x-3)
- (a) Given three points A (3,3) B (-3,1) C (-1,-1) and D (1,-7)
- Show that the line through A,B, And CD are perpendicular to each other
- Find equation of the line through point (-4,5) which is parrralel to BC
- (a) The fifth and the eleventh term of an arithmetic progression are 8 and -34 respectively. Find the sum of the first ten terms
(b) Prove that the interior angle of a cyclic quadrilateral is equal to the opposite interior angle
- (a) Mayele bought 3 bottles of juice of capacity 350ml and Dialo bought 1 bottle of juice of capacity 1 Litre
- Who had more juice to drink
- Bu how much more?
(b) Simplify the sum of 85% of 9861 and 3/5 of 12458. Write your answer to two significant figures.
SECTION B. 40 MARKS
- (a) in a certain research the data were summarized as shown on the table below
| Class mark | 10 | 15 | 20 | 25 | 30 | 35 |
| frequency | 3 | 2 | 10 | 5 | 4 | 1 |
By using the data above reconstruct a frequency distribution table including class interval and frequency
(b) Prove that equal chords of a circle subtends equal angles at the centre
- (a) solve for the quadratic equation x2-8x+7=0
(b) Solve for x and y if ![]()
- (a) (i) without using table . Draw the graph of
F(x)=x2+2y-4
(ii) State domain and range of f(x)
(b) A field is 10M longer than its width. The area is 7200m2 . Find its width
- (a) The product of a three terms of geometric progression G.P is 8000. If the first term is 4. Find the second term and third term
(b) Amina invested a certain amount of money in a serving bank whose interest rate was 10% compounded annually. After two years she got 5000.
- How much did she invest at the start
- How much did she receive as interest at the end of two years?
FORM THREE MATHEMATICS EXAM SERIES 166
FORM THREE MATHEMATICS EXAM SERIES 166
PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM THREE
MID-TERM EXAMS MARCH – 2023
041
Time: 3Hours
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in sections A and B
- Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answer for each question must be shown clearly
- NECTA mathematical tables and non-programmable calculator may be used
- All communication devices and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s)
SECTION A: (60 Marks)
Answer all questions from this section
1. (a)The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7am at what time do they change simultaneously again?
(b) If x = 0.567567567 and Y = 0.83 by Converting these decimal to fractions, find the exact value of
2. (a) If Find the value of t
(b)Write ‘L’ in terms of M1 N and T from the formula
(c)Determine the value of x if
3. (a)If the 5th term of A.P is 23 and 12th term is 37 find the first term and common difference
(b)How many years would one double one’s investment if Tsh 2500 is invested at 8% compounded semi-annually
4. (a)Find value of x and y if
(b)Let U be universal set and A and B be the subsets of U where
U = {a, b, c, d, e, f, g, h} A={c, g, f} and B= {b, d, h}
(i) Find the number of sub sets of set A'
(ii) Find n (A'n B')
(iii) If an element is picked at random from universal set (U), find the probability that it is an element of set B
5. (a)The coordinate of P, Q and R are (2, m), (-3, 1) and (6, n) respectively. If the length of PQ is units and midpoint of QR is
find possible value of m and n
(b)The gradient of line L, is – 2, another line L2 is perpendicular to L1 and passes through (-3, -2) what is the equation of L2
6.
(a)If = 17cm,
=8cm,
= 12cm, and angle ABD = 90°. Calculate the length
(b)(i) Given where
and
are the sides of Triangle ABT and
are sides of triangle KLC. What does this information imply?
(ii)A regular Hexagon is inscribed in a circle, if the perimeter of the hexagon is 42cm, find the radius of circle and its area.
7. (a)Rationalize the denominator of
(b)Without using mathematical tables find value of 3 log5 + 5log2 – 2log2
8. (a)Solve for x in the inequality 3x – 4 ≥ x + 16
(b)Solve the following pairs of simultaneous equation by elimination method
9. (a)The sum of first six terms of an AP is 72 and the second term is seven times the fifth term
(i) Find the first term and the common difference
(ii) Find the sum of first ten terms
(b)Find the sum of the first four terms of a geometric progression which has a first term of 1 and common ration of
10. (a)The gradient of line L1 is -2, another line L2 is perpendicular to L1 and Passes through point (-3, -2) what is the equation of L2?
(b)The area of the triangle ABC is 140cm2, AB=20, AC=14cm find the angle BAC
SECTION B (40 Marks)
Answer all questions
11. (a)The number of workers absent in 52 working days is given in a cumulative frequency table below
| No. of Absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 – 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find.
(i) Percentage of Workers who are at least for 20 days
(ii) Median
(b)Find the angle x in figure below
12. (a)The function f is defined as follows
- Sketch graph of f(x)
- Determine Domain of f(x)
- Determine the range of the function
(b)In a triangle ABC the ratio of angle is A: B: C = 2:3:7 the length of shortest side = 5cm. Find the length of longest side.
13. (a)Find the first term and common difference of an AP whose 5th term is 21 and 8th term is 30
(b)Find the 10th term of a sequence whose first three consecutive terms are 5, 15 and 45. Leave your answer in exponents
14. (a)Mr.Ogango from Kenya visited Tanzania. He had 5,000 Kshs and wanted to change the money into LIS dollar. If 1 Us dollar was equivalent to 2500 Tanzania shillings (Tshs) AND Ksh 1 was equivalent to Tshs 20 how much Us dollars did he get.
(b)A gardene has found that the time cut grass on a square field varies directly on the square of its length (L) and inversely as the number of men (m) doing that job. If 5 men cut grass on field of size 50m in 3 hours, how many more men are required to cut grass on a field of side 100m in 5 hours. Assume
FORM THREE MATHEMATICS EXAM SERIES 125
FORM THREE MATHEMATICS EXAM SERIES 125
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
MID TERM EXAMIATIONS
024 MATHS- THREE
Duration: 2:30 Hours
INSTRUCTIONS.
- This paper consists of two sections A and B.
- Answer all questions in section A and only Four Questions in Section B
- All writing must be in blue or black ink except drawing which must be in pencil.
- Calculators, cellular phones and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number at the top right corner of every page.
- Show clearly all working for each question
SECTION A( 60 %)
- a) 468 – 468 ÷39 + 39 correct to two significant figures
b) Calculate without using mathematical tables
![]()
2. Make x subject of the formula
P=![]()
3. By using the substitution t=3x, solve the equation 32(1+x) – 3x=3(x+3)-3
4. The size of exterior angle of a regular polygon is 450. Find :
i) The number of sides
ii) The sum of all interior angles
5. Find the values of x that satisfy the following equation log(x+5) + log(x + 2)=log4
6. A translation T carries the point (1,2) to (-2,8). Find where it map :
a) Pont A(-2,2)
b) The origin
7. The lines with equations 2x=3 – y and 2y + 3x=4 meet at point Q. Find the coordinate of point Q.
8. Find two consecutive odd numbers whose product is 195.
9. In a class of 31 students, 17 participate in English debate, 12 participate in English and Sports. If every student is required to participate at lest one of the two events. Find the number of students who participate in i) Sport ii) English only.
10. A dealer bought 10 books for 400,000/=. He sold 2/5 of them at 40,000/= shillings each and the remaining at 60,000/= shillings each. What was the percentage profit?
SECTION B(40%)
11. The examination scores in Basic Mathematics of 40 students are given in the following cumulative frequency table.
| Class Interval | 10 - 19 | 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | 60 - 69 |
| Cumulative Frequency | 3 | 6 | 12 | 22 | 35 | 40 |
a) Find the mean using Assumed mean A=44.5
b) Calculate median
c) Draw histogram and use it to estimate Mode
12. a) Consider the figure below where PQ//BC.
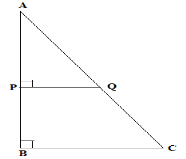
i)Prove that triangle ABC is similar with triangle APQ
ii) If the length of BC=15, PQ=9cm and PB= 6cm. Find the length of AP.
b)Prove that, the sum of two angles of a triangle is equal to exterior angle of the third angle.
13. a) Find the expressions which describe the relation of the graph below
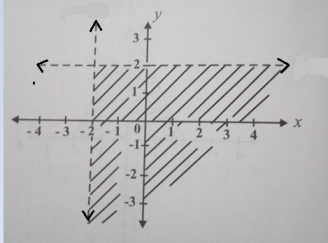
b) Determine Domain and range of this relation.
c) Find inverse of this relation.
14 a) Given f(x) = -x2 + 4x – 5. Find
i) Axis of symmetry
ii) Maximum or minimum value
iii) Turning point
b) Draw the graph of f(x) and use it to solve the equation -x2 + 4x -15 =0
15.The function f is defined as follows:
F(x) = 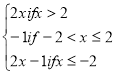
![]()
i) Sketch the graph of f(x)
ii) Determine domain and range
iii) Find
(a) f(1) b) f(-4) c) f(π)
16. Given: Opening Stock 01/01/2012 34,430/=
Closing Stock 31/12/2012 26,720/=
Net purchases during 2012 212,290/=
Expenses for the year 45,880/=
Gross profit is 45% of cost of sold goods.
Find a) Average Stock b) Cost of Sold Goods c) The gross profit d) Net Profit
FORM THREE MATHEMATICS EXAM SERIES 7
FORM THREE MATHEMATICS EXAM SERIES 7
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256