FORM THREE MATHEMATICS EXAM SERIES 235
FORM THREE MATHEMATICS EXAM SERIES 235
PRESIDENT’S OFFICE REGIONAL, ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM THREE ANNUAL EXAMINATION
041 BASIC MATHEMATICS
TIME:3 HOURS NOV, 2023
INSTRUCTION
- This paper consist of two sections A and B
- Answer all questions
- Calculators and mathematical tables may be used
- All diagram must be drawn by using pencil
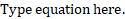
- All writing must be in a blue or black ink
SECTION A (60 MARKS)
- (a)Write 490.032578 correct to
- 5 significant figure
- Thousandths
- 4 decimal places
(b)The anterior angle of a regular polygon is four times as its exterior angle. Find
- Size of each exertion angle
- Number of sides
- State name of polygon
- (a)Solve the following exponential equation
![]()
(b)Given log 52 = 0.4307 and log 53 = 0.6826
- (a)A painter placed 20m ladder against the wall of a house so that the base of the ladder is 4m away from the wall. How high does the ladder touch the wall from the ground?
(b)If ![]() Where A is an active angle find
Where A is an active angle find
- Sin A
- Cos A
- (a)If
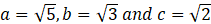 simplify
simplify 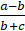
(b)Describe application of Logarithm in daily life
- (a) In following figure.
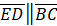 and
and 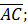 if
if 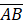 =13cm and
=13cm and 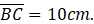 Find area of BCDE
Find area of BCDE
(b) What do the following terms mean as used in accounting
- Cash Book
- Assets
- Credit Transaction
- (a)A company bought two vans for Tshs 25,000,000/=each. If one car was sold at a profit of 18% and another was sold at a loss of 6%. In the whole transaction, there was no loss. What was profit made by the company?
(b) If the square of the hypotenuse of an isosdes right angle Triangle is 128cm2. Find the length of each side.
- (a)From the top of a tower of height 60m the angles of depression of the top and bottom of a building are observed to be 30° and 60° respectively. Find the height of the building.
(b)Three bells commerce tolling together and toil at an interval of 8, 10 and 12 seconds respectively. How many times do they together is 50minutes?
- (a) If the length of each side of a square is mix eased to 16times the area of Small Square. Find the length of one side of Original square
(b)A large rectangular garden in a park is 120m wide and 150m long. A contractor is called in to add a brick walkway to surround the garden by the same width. If the area of the walkway 2800m2 how wide is the walkway?
- (a)
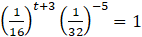 . Find the value of t
. Find the value of t
(b)Write “L” in terms of M, N and T from the formula
![]()
(c)Determine the value of x if ![]()
- (a) Let
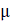 be a universal set and A and B be sub-set of
be a universal set and A and B be sub-set of 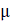 , if μ = {a, b, c, d, e, f, g, h}
, if μ = {a, b, c, d, e, f, g, h}
A = {c, g, f} and B = {b, d, h} find
- The number of sub sets of set A
- n(A'∩B)
(b)The traffic lights at three different road crossing changing after every 48 seconds, 72seconds, and 108 seconds respectively. If they change simultaneously at 7am at what time will they change simultaneously again?
SECTION B (40 Marks)
Answer all questions
- (a)The marks in Basic Mathematics terminal examination obtained by 40 students in one of secondary schools in same district were as follows.
60, 54, 48, 43, 37, 61, 43, 66, 65, 52, 37, 81, 70, 48, 63, 74, 67, 52, 48, 37, 48, 42, 43, 52, 52, 22, 27, 37, 44, 38, 29, 19, 28, 36, 42, 47, 36, 52, 50, 28.
- Prepare a frequency distribution table with class interval 10 – 19, 20 – 29, etc
- Find class that contain medium
- Find the mean
- Calculate the median
(b)Find the value of angle x in figure below, where O in the center of the circle.
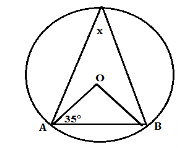
- (a) Two towns P and Q on latitude 48° are 370 nautical Milles a part. Find the difference in their longitude.
(b)A regular hexagon is inscribed in a circle. If the perimeter of hexagon is 42cm. Find the radius of the circle and its area.
- (a)If
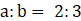 and
and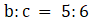 . Find
. Find 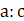 and
and 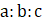
(b)From the following information given by Mbeya Co. Ltd for the year ended 31st Dec 2022.
Stock (01.01.2022) ................... Three quarter of closing
Stock (31.12.2022) .............. ![]() of Net purchases
of Net purchases
Net purchases during 2022 ................ 432.000
Gross Margin ........................... 15%
Expense .................................... 20% of Net profit
Calculate:
- Cost of good sold
- Gross profit
- Net-profit
- (a)(i) With using table of values draw the graph of
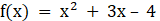
(ii) State the domain and range of f(x)
(b) Solve for x and y if
![]()
FORM THREE MATHEMATICS EXAM SERIES 151
FORM THREE MATHEMATICS EXAM SERIES 151
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
MATHS ANNUAL EXAMINATIONS
FORM THREE-2022
INSTRUCTIONS
- This paper consists of section A and B with a total of fourteen (14) questions.
- Answer all questions in both sections
- Each question in section A carries six (6) marks while each question in section B carries ten (10) marks
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables or non-programmable scientific calculator and graph papers may be used unless otherwise stated
- You are advised to spend no more than two (20 hours on section A
- All communication devices and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number on every page of your booklet(s)
SECTION A (60 MARKS)
Answer all questions in this section.
- (a) At exactly 7:00a.m, two buses leave the bus terminal. Thereafter, every 40 and 70 minutes, a bus leaves the terminal. Find the time busses will leave the terminal together.
(b)(i) Estimate the value of ![]()
(ii)Simplify the ratio of a tob, given that ![]() and b=
and b=![]() to its lowest form.
to its lowest form.
- (a) Solve for x in the equation
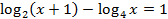
(b) If 3x – y=4, What is the value of ![]()
- A bag contains 6 red balls and 8 blue balls. A random selection of balls from the bag is performed. If one ball is selected from the bag and then replaced before selecting the second ball:
- Draw a tree diagram showing all the possible outcomes and their corresponding probabilities
- Find the probability of selecting
- Balls of different colours
- Balls of the same colour
- (a)Three consecutive vertices of parallelogram are at A(-1, 2), B(5, 1), C(6, 5), and
D(x, y), Find the coordinate of vertex D.
(b) Two towns P and Q are 30km apart, Q being due East of P. Town R is situated at a bearing of 150° from P and 240° from Q. calculate the distance RQ
- (a)P and Q are markers on the banks of a canal which has parallel sides. R and S are telegraph poles which are directly opposite each other. PQ=30m and QR=100m. When Mr. Ates walked 20m from P directly away from the bank, he reached a point T such that T, Q and S lined up. How wide is the canal?
(b)In a triangle ABC, angle ABC=50° and point X lies on ![]() such that
such that ![]() with the aid of a diagram, calculate
with the aid of a diagram, calculate ![]()
- (a)An English family on holiday in France exchanged 450 for euros when the exchange rate was 1.41 euros to the pound. They spent 500 euros and then exchanged the rest back into pounds, by which time the exchange rate had become 1.46 euros to the pound. How much did the holiday cost? (Give your answer in pounds.
- The following balance sheet relates to Mr. Max Malipo, a trader, as at 31st December 2020
MR. MAX MALIPO
| PARTICULARS | AMOUNT | PARTICULARS | AMAUNT | ||
| CAPITAL Add: Net Profit
Less: Drawings
LIABILITIES Creditors Salaries Accrued Tel. Outstanding | 179,000 30,280 |
191,280
7,000 5,000 220 | ASSETS Furniture Machinery Debtors Cash at Bank Rates Prepaid Closing Stock |
|
40,000 30,000 10,000 3,000 500 120,000
|
| 209,280 18,000 | |||||
|
| |||||
| 203,500 | 203,500 | ||||
Use the information given in the balance sheet above to find:
- Total Fixed Assets
- Total Current Assets
- Total Current Liabilities
- Working Capital
- (a)Mr. Cathbert starts an employment with a monthly salary of 340,000/= Tshs and receives an increment of 12,000/= Tsh every year.
- What will be his salary in the fourteenth year of employment?
- After how long would he be earning 592,000 Tsh per month?
(b)The sum of the first two terms of a geometric progression is 27 whereas the sum of the 2nd and 3rd term of the same progression is 54. Find the first term and the common ratio.
- (a)At a point 200m from the foot of a tower on a level road, the angle of elevation of the top of the tower is 58°.
- Represent this information diagrammatically,
- Find the height of the tower.
(b)A rectangular frame ABCD, 48cm by 55cm, is made from wire. The diagonals of the frame are also made from wire.
Calculate the total length of wire needed to make the frame and the diagonals.
- (a)Find the values of m and n in system of linear equations
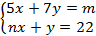
(b)Find the values of a andb if (ax + 5) (bx + 4) = 21x2 + 43x + 20.
SECTION B (40 Marks)
Answer all questions in this section
- (a)The table below shows the distribution of marks scored by 45 students in Physics examination
| Marks (in %) | 99 – 89 | 88 – 78 | 77 – 67 | 66 – 56 | 55 – 45 |
| Number of students | 2 | 5 | 20 | 11 | 7 |
- Determine the median class of marks
- Compute the mean mark
- Draw the histogram and hence use it to estimate the mark scored by many students
(b) ![]() are secants that intersect at A in the figure below. Given that chords
are secants that intersect at A in the figure below. Given that chords ![]() Find the angles x and y.
Find the angles x and y.
- (a)A circular tank has a base of 53-metre radius and height of 12 metres. If the tank is a half full of water, what is the volume of water in a tank? Give your answer in litres (1 cubic metre = 1000 litres)
(b)Mr. Paul went to buy a car. He wanted to buy a car that has not covered more than 2,500 kilometres (not much used). If he found only one car in the market which travelled from Nairobi (56°N, 40°E) to Dar-es-Salaam (26°N, 40°E). What can you advice Mr.Paul according to his need? (Use radius of the Earth, RE= 6370km)
- (a)Find value of K if the matrix
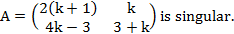
(b)Use inverse matrix method to solve for x and y in the following pair of equations of straight lines: ![]()
(c) A linear transformation T maps ![]() .
.
Find
- The transformation matrix T
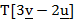
- (a)Find the role of the following is solving linear programming problems:
- Non-negativity constraints
- Feasible region
- Objective function
(b) MzeeMalengo has 240 acres of land which he wants to plant maize and oats. For each acre of maize planted he will profit 400,000/= Tsh, and for each acre of oats planted he will profit 300,000/= Tsh. However, maize takes 2 hours to harvest, while oats require 1 hour harvesting, and he has only 320 hours available for harvesting. How many acres of each crop should he plant in order to maximize profits?
FORM THREE MATHEMATICS EXAM SERIES 113
FORM THREE MATHEMATICS EXAM SERIES 113
THE UNITED REPUBLIC OF TANZANIA PRESIDENT'S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM THREE ANNUAL EXAMINATION
041 BASIC MATHEMATICS
Time 3:00 Hours Year: 2022
INSTRUCTIONS
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions
- Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- Mathematical tables and non-programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room
- Where necessary, use the following constants
- Pie,
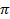 =3.142
=3.142 - Radius of the earth, Re =6400km.
SECTION A: (60 MARKS)
Answer all questions from this section
1. (a)The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m at what time they change simultaneously again?
(b) If x = 0.567567567… and y = 0.8![]() by converting these decimals to fractions, find the exact value of
by converting these decimals to fractions, find the exact value of ![]()
2. (a) If ![]() find the value of t
find the value of t
(b)Write “L” in terms of M, N and T from the formula ![]()
(c) Determine the value of x if ![]()
3. (a)Let ![]() be a universal set and A and B be the subsets of
be a universal set and A and B be the subsets of ![]()
A= {c, g, f} and B= {b, d, h} find
(b) Given that A= {x : 0 ≤ x ≤ 8}
B = {x : 3 ≤ x ≤ 8}
where x is an integer, in the same form, represent in a Venn diagram
- A u B
- A n B
and hence find the elements in each set.
4. (a) Find the slope of a straight line which passes through points A (0, a) and B(3a,0)
(b) The co-ordinates of the square PQRS are given by P(1, 4), Q(3, 4), R(3, 2), and S(1, 2). Write the co-ordinates of the image of the square P’Q’R’S’ under reflection in the x-axis.
5. (a) Given ![]() where
where ![]() are the sides of the triangle ABT and
are the sides of the triangle ABT and ![]() Are sides of the triangle KLC. What does this information imply?
Are sides of the triangle KLC. What does this information imply?
(b) Calculate the area of the following figure, if 0 is the centre of the circle and OABC is a square.
6. (a)Twelve people can dig a trench in 15 days for 8 hours daily. How long can they take to finish the same work, working for 10 hours daily?
(b)A variable V varies jointly as the variable A and h. when A=63 and h=4, v=84.
Find;
- V when A=9 and h=7
- A when V=4.5 and h=0.5
7. (a)If a:b=2:3 and b:c=5:6. Find a:c and a:b:c
(b) PQR is an isosceles triangle whereby PQ =PR and QS = SR. If S is a point between Q and R prove that Δ PQS ≡ ΔPRS
8. (a)If the 5th term of an arithmetic progression is 23 and the 12th term is 37, find the first tem and the common difference.
(b) In how many years would one double one’s investment if Tshs 2500 is invested at 8% compounded semi –annually.
9. (a) Given that
![]()
Find :
(i)![]()
(ii)![]()
(b) A and B are two points on the ground level and both lie West of flagstaff. The angles of elevation of the top of the flagstaff from A is 56° and from B is 43°. If B is 28m from the foot of the flagstaff. How far apart are the point A and B?
10. (a)Solve for the quadratic equation x2 – 8x + 7=0
(b)Solve for x and y if ![]()
SECTION B (40 MARKS)
Answer all questions from this section
11.The marks in basic Mathematics terminal Examination obtained by 40 students in one of the secondary school in Katavi were as follows;
60, 54, 48, 43, 37 61, 43, 66, 65, 52, 37, 81, 70, 48, 63, 74, 67, 52, 48, 37, 48 42, 43, 52, 52, 22, 27, 37,44 38, 29, 19, 28 36, 42, 47, 36, 52, 50, 28.
- Prepare a frequency distribution table with class intervals 10 – 19, 20 – 29, etc.
- Find the class which contain the median
- Find the mean
- Calculate the median.
12. (a) From the following information given by Mbeya Co.ltd for the year ended 31st December 2021.
Stock (01.01.2021) ………………………….Three quarter of the closing stock
Stock (31.12.2021) ………………………… ![]() of net purchase
of net purchase
Net purchases during 2021 …………………. 432,000.
Gross margin …………………………. 15%
Expenses ……………………………… 20% of Net profit
Calculate;
- Cost of goods sold
- Gross profit
- Net profit
(b) State Three uses of the trial balance
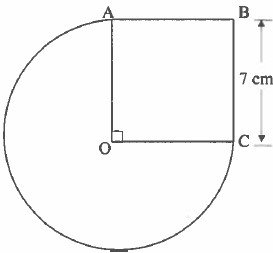
13. (a) Find the value of angle x in the figure below, where O is the centre of the circle
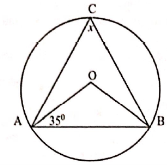
(b)Two places P and Q both on the parallel of latitude 26°N differ in longitudes by 40°, find the distance between them along their parallel of latitude.
14. Given
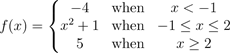
(i) Sketch the graph of f(x).
(ii) State the domain and range of f(x) .
(iii) Is f(x) a one-to-one function? Give reason(s).
FORM THREE MATHEMATICS EXAM SERIES 103
FORM THREE MATHEMATICS EXAM SERIES 103
PRESIDENT'S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
Time: 3 Hours November 2020 a.m.
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions.
2.Answer all questions in sections A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
3.All necessary working and answers for each question must be shown clearly.
4.mathematical tables may be used.
5.Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
SECTION A (60 Marks)
Answer all questions in this section.
1.a) Use mathematical table, evaluate
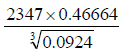
(b)Express 5.4545454545... in form of a/b where a and b are both integers.
2.(a)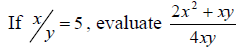
b)Solve for x the following equation 32x-3 X 8x+4 = 64 ÷ 2x
c)Rationalize the denominator
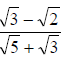
3.a) Find value of P which makes the following equations perfect square
i) x2 + 8x +P=0
ii) x2 - ![]() x + P=0
x + P=0
b) Solve for x the equation
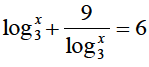
4.a)Given the universal set U={p, q, r, s, t, x, y,z} A={p, q, r, t} B={r, s, t, y }.
Find i)(AUB) ii)(A’nB’)
b)In a class of 60 students, 22 students study Physics only, 25 study Biology only and 5 students study neither Physics nor Biology. Find i) Number of students study Physics and Biology. ii) Number of students that study Biology.
5.a) A, B and C are to share T.sh 120,000/= in the ratio of![]() :
:![]() :
: ![]() . How much will each get?
. How much will each get?
b)A radio is sold at T. sh 40,500/= this price is 20% value added tax(V.A.T). Calculate the amount of V.A.T.
6.(a) Triangles ABC and STBare similar. AB=3cm and ST=2cm. The area of triangle STU is 6cm2. Find the area of triangle ABC
(b) The translation T maps the origin onto a point P(4,8). Where will T map the points: (i) Q(0,4)?
(ii) N(−10,8)
7. (a) Find the equation of the line through the point (2,−2) crossing the ![]() -axis at the same point as the line whose equation is y= x−4
-axis at the same point as the line whose equation is y= x−4
(b) A farmer sold a quarter of his maize harvest and give one third of the remaining to his relatives.If the farmer remained with 36 bags of maize, find:- (i) How many bags of maize did the farmer harvest. (ii) How many bags of maize did the farmer sold.
8.(a) The sum of 1st n-terms of certain series is 2n-1, show that this series is Geometric Progression. Find an the nth term of this series.
(b) )The 5th term of A.P is 23 and the 12th term is 37. Find
(i)The tenth term
(ii)The sum of the first tenth terms by using the values computed above without using the common difference for this progression
9.(a) Given that
Find The value of
![]()
(b) A man standing on top of cliff 100m high, is in line with two buoys whose angles of depression are 170 and 210. Calculate the distance between the buoys.
10. a)Solve for x if
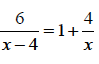
(b) A two-digit of positive number is such that, the product of the digits is 8. When 18 is added to the number, then the digits are reversed. Find the number.
SECTION B (40 MARKS)
Answer All Questions In This Section
11. The daily wages of one hundred men are distributed as shown below
| Wages in T.Sh. x 1,000 | 3.0 - 3.4 | 3.5 - 3.9 | 4.0 - 4.4 | 4.5 - 4.9 | 5.0 - 5.4 | 5.5 - 5.9 | 6.0 - 6.4 | 6.5 - 6.9 |
| Number of men | 4 | 6 | 10 | 14 | x | 20 | 14 | 6 |
a)Find the value of x
b)Calculate the daily mean wage of the 100 men
c)Draw histogram to represent this data and use it to estimate Mode
d)Draw cumulative frequency curve and use it to represent Median
12.(a ) Find values of angles marked x0 and y0 in the figure below
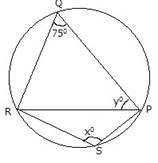
(b)Prove that exterior angle of cyclic quadrilateral is equal to interior opposite angle.
(c)Two places P and Q both on the parallel of latitude 260N differ in longitude by 400. Find the distance between them along their parallel of latitude
13. .(a)Prepare Balance sheet of Mr. Hamis from the following Assets and Liabilities on 31 st December 2009:
•Creditors 100,000/=
•Debtors 150,000/=
•Bank Overdraft 50,000/=
•Cash in hand 15,000/=
•Stock 85,000/=
•Furniture 42,000/=
•Premises 250,000/=
•Capital 392,000/=
(b) Use the transactions above to find
i.Total current asset
ii.Total Current liability
iii.Working Capital iv. Total fixed Asset
14. a) The function f is defined as follows:
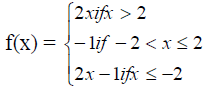
i) Sketch the graph of f(x)
(ii) Determine domain and range (
(iii) Find f(1) , f(-4) and f(π)
(b)For what values of x is function f(x)=![]() is undefined?
is undefined?
FORM THREE MATHEMATICS EXAM SERIES 39
FORM THREE MATHEMATICS EXAM SERIES 39
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256