PRESIDENT’S OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
SECONDARY SCHOOL EXAMINATION SERIES
MATHEMATICS FORM TWO
PRE-NECTA – 2025
041
Time: 2:30 Hours AUG, 2025
INSTRUCTIONS
1. This paper consists of a total ten (10) compulsory questions
2. Show your work clearly
3. All writing must be in blue or black ink, except drawings which should be in pencil
4. All communication devices, programmable calculators and any unauthorized materials are not allowed in the examination room
1 a) The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 10 seconds respectively. If they change simultaneously at 7a.m at what will they change simultaneously again?
b) If x = 0.567567567... and y – 0.83 by converting these decimals to
fractions, find the exact value of ![]() in simplest form
in simplest form
2 a) If T= 
Find the value of t
b) Write ‘’L’’ in terms of M, N and T from the formula =

c) Determine the value of x if log5(x+1)-1=log5(x-3)
3. a) A lorry carries 7.2 tonnes of sand from the mining area to the industrial site. One the way 230kg of sand either fall off or blow away. What mass of sand will remain by the end of the journey? Give the answer in tonnes b) An article was sold for sh 160,000 at a profit of 25% find the buying price
of the article
4. a) Solve for the quadratic X2 – 8x +7 = 0
b) Solve for x and y if;

5. a) The sum of two numbers is 127. If the difference/ between numbers is 7, find the numbers.
b) If : = 2:3 𝑎 : = 5:6 find : 𝑎 :: 6.
6. a) Rationalize the denominator and simplify:
b) Find the area of an equilateral triangle whose sides are 20cm
7. a) A certain amount of money was divided in the ratio 2:3:5. If the difference between the largest share and the smallest share was sh 7,500/=, find the largest share
b) Find the x – intercept of a line through points (-3,5) and (0, -1)
8. a) The scale of map is 1cm to 10km. find the distance on the map between two towns which are:
(a) 20 km apart (b) 48.5 km apart
9. a) Use the following figure to find the values of x and y

b) Find the value of each of the following expressions and simplify the
answers

10. In a class of 45 pupils, 25 takes History, 27 takes Commerce. If the total number of those who takes History and Commerce is 37, find:
a) The number of pupils who takes both History and Commerce
b) The number of pupils who takes History only
c) The number of pupils who takes neither History nor Commerce
FORM TWO MATHEMATICS EXAM SERIES 215
FORM TWO MATHEMATICS EXAM SERIES 215
THE UNITED REPUBLIC OF TANZANIA
PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCY BASED EXAMS
FORM TWO PRE-FTNA ASSESSMENT
041 BASIC MATHEMATICS
TIME: 2:30 hours October, 2022
Instructions
- This paper consists of 10 questions.
- Answer all questions.
- Cellular phones are not allowed in the Examination rooms.
- Write you examination number on every page of your answer sheet(s)
| FOR EXAMINER’S USE ONLY | ||
| QUESTION NUMBER | SCORE | EXAMINER’S INITIAL |
| 01 |
|
|
| 02 |
|
|
| 03 |
|
|
| 04 |
|
|
| 05 |
|
|
| 06 |
|
|
| 07 |
|
|
| 08 |
|
|
| 09 |
|
|
| 10 |
|
|
| TOTAL |
|
|
| CHECKER’S INITIAL |
|
|
- (a)( i) Find the sum of all prime numbers between 3 and 23 inclusively.
(ii) When two different signs are multiplied, a product is obtained. Multiply the product obtain with a negative sign. Give the last sign you Will obtain.
- Change 0.
 into a simplest fraction then express your answer into percentage
into a simplest fraction then express your answer into percentage
- (a) Write 0.07
 correct to
correct to
(i) Four significant figures
(ii) Four decimal places
(b) write 20.025 into hundredth.
(c) Aisha’s mom took 30 minutes to cut the vegetables, and she took 1 hour in cooking. Find how many Seconds she took to complete the whole cooking?
3. (a) In the figure below M<RTS = 80
FORM TWO MATHEMATICS EXAM SERIES 131
FORM TWO MATHEMATICS EXAM SERIES 131
THE UNITED REPUBLIC OF TANZANIA
PRESIDENT’SOFFICEREGIONALADMINISTRATIONANDLOCALGOVERNMENT
COMPETENCY BASED EXAMS
FORM TWO PRE-FTNA ASSESSMENT
041 BASIC MATHEMATICS
TIME:2:30hours October,2022
Instructions
- This paper consists of 10 questions.
- Answer all questions.
- Cellular phones are not allowed in the Examination rooms.
- Write you examination number on every page of your answer sheet(s)
| FOR EXAMINER’S USE ONLY | ||
| QUESTIONNUMBER | SCORE | EXAMINER’S INITIAL |
| 01 | ||
| 02 | ||
| 03 | ||
| 04 | ||
| 05 | ||
| 06 | ||
| 07 | ||
| 08 | ||
| 09 | ||
| 10 | ||
| TOTAL | ||
| CHECKER’S INITIAL | ||
- (a)( i) Find the sum of all prime numbers between 3 and 23 inclusively.
(ii) When two different signs are multiplied, a product is obtained. Multiply the product obtain with a negative sign. Give the last sign you Will obtain.
- Change 0.
 into a simplest fraction then express your answer into percentage
into a simplest fraction then express your answer into percentage
- (a) Write 0.07
 correct to
correct to
(i) Four significant figures
(ii) Four decimal places
(b) write 20.025 into hundredth.
(c) Aisha’s mom took 30 minutes to cut the vegetables, and she took 1hour in cooking. Find how many Seconds she took to complete the whole cooking?
3. (a) In the figure below M<RTS = 80
FORM TWO MATHEMATICS EXAM SERIES 129
FORM TWO MATHEMATICS EXAM SERIES 129
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
ANNUAL EXAMINATION
FORM TWO
BASIC MATHEMATICS
041
TIME: 2:30 HOURS November, 2021
![]()
Instructions
1. This paper consists of ten (10) compulsory questions.
2. Answer ALL questions
3. Each question carries ten (10) marks.
4. Show clearly all the workings and answers in the spaces provided.
5. All writings must be in blue or black ink except for drawings which must be in pencil.
6. Four figures/mathematical tables, geometric instruments and graph papers may be used where necessary.
7. Calculators, cellular phones and any unauthorized materials are not allowed in the examination room.
8. Write Your Examination Number at the top right corner of every page.
| FOR EXAMINER’S USE ONLY | ||
| QUESTION NUMBER | SCORE | EXAMINER’S INITIALS |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| TOTAL |
|
|
| CHECKER’S INITIALS |
| |
1. (a) Three bells ring at intervals of 20 minutes, 30 minutes and 40 minutes. If they start ringing together at 7.30 am
(i) After how long will they ring together again?
(ii) At what time will this be?
(b) Round off 349.678 to the nearest.
(i) Tens
(ii) Hundredth
(iii) One significant figure
2. (a) Write ![]() in form of
in form of ![]() , where b ? 0.
, where b ? 0.
(b) In a class of 40 students ![]() are boys. Two fifth of the girls wear spectacles.
are boys. Two fifth of the girls wear spectacles.
How many girls do not wear spectacles?
3. 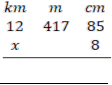 (a) Perform:
(a) Perform:
(b) Find the time in which sh 200,000/= will earn sh 48,000/= at the rate of 4% interest per annum.
4. (a) Calculate the angles marked with letters X, Y and Z.

(b) Find the area of rectangle whose perimeter is 30cm and its length and width are (3W-7) cm and (W+2) cm respectively.
5. (a) Factorize the expression
6x2 – 11x + 4 by splitting the middle term.
(b) The sum and difference of the two numbers are 9 and 3 respectively. Find the possible numbers.
6. (a) (i) Find the equation of the straight line passing through (3,5) and (7,9).
(ii) Calculate the gradient and coordinates of the y-intercept of 2x+3y=12.
(b) Find the image of a point (-4, 3) after a reflection on y-axis followed by another reflection on y=0.
7. (a) If ![]() -4x+2 =
-4x+2 = ![]() 9. Find the value of X.
9. Find the value of X.
(b) Rationalize ![]() writing the answer in the form a
writing the answer in the form a![]() where a, b, c and d are real.
where a, b, c and d are real.
(c) Given log2 = 0.3010, log3 = 0.4770 and log7 = 0.8451. Find the value of log294.
8. (a) Calculate the length of EC and CD in figure below:
B D
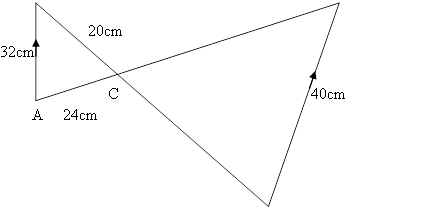
E
8. (b) Use the figure below to prove that triangle ADB? Triangle ADC
A
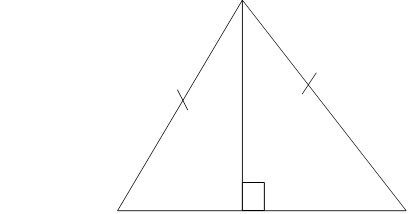
C D B
9. (a) A rectangle has sides of 12mm and 16mm. Calculate the length of one of its diagonals.
(b) Calculate the exact value of ![]() .
.
10. (a) In the Venn diagram below:
U = { Boys in form II at a certain secondary school}
F = { Members in the football team}
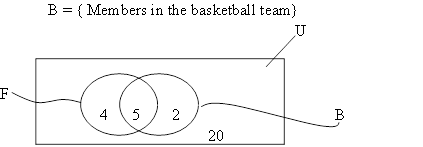
(i) How many boys are in the football team?
(ii) How many boys are in both teams?
(iii) How many are in the football team but not in the basketball team?
(iv) How many are neither basketball nor football team?
(v) How many boys in form II at the school?
10. (b) The table below shows the distribution of the score of 60 students in Mathematics table at MJI MWEMA secondary school.
| Marks % | 45 – 55 | 56 – 66 | 67 – 77 | 78 – 88 | 89 - 99 |
| No. of students | 11 | 15 | X | 17 | 10 |
(i) Find the value of X.
(ii) Find the percentages of the student score ate most 77 marks.
FORM TWO MATHEMATICS EXAM SERIES 73
FORM TWO MATHEMATICS EXAM SERIES 73
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256