THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL OF TANZANIA
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2021
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (()6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) Find the lowest common multiple of the numbers 15, 35 and 40.
View Ans
(b) Find the approximate value of the expression by rounding off each number in the expression
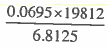
to one significant figure.
View Ans
2. (a) Express the equation 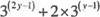 = 1 in terms of P given that P = 3y.
= 1 in terms of P given that P = 3y.
View Ans
(b) Determine the value of y in the equation
log10(3y+2) - 1=log10(y-4)
View Ans
3. In a class of 45 students, 30 study Chemistry, 20 study Physics and 5 study neither of the two subjects.
(a) Represent this information in a well labeled Venn diagram.
(b) Using part (a) find:
(i) the number of students studying both subjects.
(ii) the probability that a student selected at random from the class will be studying Chemistry only.
View Ans
4. (a) An engineer is in the process of constructing two straight roads, RI and R, which will meet at the right angles. If RI will be represented by the equation 2x—3y—4=0 and R, will pass through the point , find the equation representing R2 in the form ax+by+c=0
View Ans
(b) A boat crosses a river at a velocity of 30 km/h southwards. Water in the river flows at 5 km/h due East. By using the knowledge of vectors, calculate the resultant velocity of the boat. Give the answer correct to 2 decimal places.
View Ans
5. (a) The lengths of two similar rectangles are 6 cm and 8 cm. If the area of the small rectangle is 73.8 cm2 , find the area of the large rectangle.
View Ans
(b) The exterior and interior angles of a regular polygon are in the ratio 2:4 respectively. Find the number of sides of the polygon.
View Ans
6. (a) A piece of length 7.42 m is cut off from a string that is 13.5 m long. If the remaining part of the string is divided into equal pieces of length 32 cm, how many pieces are there?
View Ans
(b) The mass (M) which can be supported by a beam varies directly with the breadth (b) and inversely with the length (l). If a beam of breadth 2 m and length 15 m can support a mass of 200 kg, what mass can be supported by a beam which is 3 m broad and 20 m long?
View Ans
7. (a) What do the following terms mean as used in Accounts?
(i) Trading account
(ii) Profit and loss account
(iii) Balance sheet
(iv) Cash account
View Ans
(b) A car which its buying price was shs 12,500,000 was sold at a loss of 20 percent. Find the loss made and selling price.
View Ans
8. (a) A farmer wants to plant 6 mango seedlings in a row at a fixed interval of 7 metres.
Determine the length of the row.
View Ans
(b) If the fifth and the sixth terms of a Geometric Progression (G.P.) are 162 and 486 respectively, find the common ratio and the first term of the G.P.
View Ans
9. (a) Show that cos(900 +θ)= -sin θ
View Ans
(b) In triangle UVW, UV =3cm and UW = 5 cm . If the angle formed between the two sides is 600 , find WV correct to two decimal places.
View Ans
10. (a) A trapezium has the area of 2x2 - 8x+6 square units. If the parallel sides are (2x+3) units and (2x - 7) units long, find its height.
View Ans
(b) The difference between two positive numbers is 7. If their product is 30, find the numbers.
View Ans
SECTION B (40 Marks)
Answer all questions in this section.
l l . The following are the marks obtained by 40 students in one of the Basic Mathematics examinations:
| 48 | 47 | 57 | 56 | 71 | 62 | 46 | 45 | 50 | 76 |
| 58 | 66 | 48 | 32 | 89 | 60 | 42 | 47 | 54 | 67 |
| 64 | 49 | 37 | 64 | 67 | 44 | 45 | 45 | 42 | 34 |
| 47 | 44 | 73 | 44 | 58 | 43 | 54 | 35 | 54 | 52 |
(a) Prepare a frequency distribution using the information: number of classes = 8; size of each class = 8 and the lower limit of the first class interval = 32.
View Ans
(b) Use the frequency distribution obtained in part (a) to find the actual mean when the assumed mean is 83.5.
View Ans
(c) Calculate the difference between the actual mean and the median of this distribution. Hence, comment on the difference obtained.
View Ans
12. The following rectangular block is 8 cm long, 6 cm wide and 5 cm high.
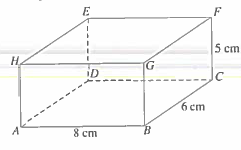
(a) Name the angles formed between line AG with the planes ABCD and BCFG.
(b) Calculate:
 the length of AC.
the length of AC.
(ii) the length of AF. (iii) the size of angle CAF.
View Ans
(c) A ship sails from point A(100 S, 300 W) to point B(110 N, 300 W) at a speed of 900 km/h. If it leaves point A at 10:00 am, when will it arrive at B? (Radius of the Earth (R) = 6400 km).
View Ans
13. (a) Solve the following system of simultaneous equations by using the matrix method.
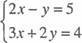
View Ans
(b) Triangle ABC has the vertices A (l , l ), B (2, 4) and C (5, 3). Find the vertices of its image under the transformation matrix
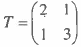
View Ans
(c) Find the image of the point A(4, 2) after a rotation about the origin through 1200 anticlockwise.
View Ans
14. (a) Jennifer makes two types of garments, Batiki and Kitenge. Batiki requires 2.5 metres of material while Kitenge requires 2 metres of material. The business uses up to 400 metres of materials daily for the production of both types of garments but produces at most 80 metres of Batiki and at least 60 metres of Kitenge daily. Taking x to represent the number of Batiki and y the number of Kitenge produced daily;
(i) write down the inequalities satisfying the given information.
(ii) find the number of each type of garments the business can produce in order to get the maximum income if the income is given by f (x, y) = 300x+ 200y .
(b) What is the importance of studying linear programming? Give 2 points.
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256