THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Wednesday, 02nd November 2016 a.m.
Instructions
1. This paper consists of sections A and B.
2. Answer all questions in section A and four (4) questions from section B. Each question in section A carries six marks while each question in section B carries ten (10) marks.
3. All necessary working and answers for each question done must be shown clearly.
4. Mathematical tables may be used.
5. Calculators and cellular phones are not allowed in the examination room.
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) From the set of numbers {1, 3, 4, 5, 6, 8, 10, 15, 17, 21, 27}; write down:
(i) the prime numbers, (ii) the multiples of 3, (iii) the factors of 60.
View Ans
(b) Four wooden rods with lengths of 70 cm, 119 cm, 84 cm and 105 cm are cut into pieces of the same length. Find the greatest possible length for these pieces if no wood is left over.
View Ans
2. (a) Solve for x in the equation 9(x−3) × 81(1−x) = 27−x .
View Ans
(b) Show that
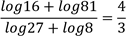
View Ans
3. (a) By substituting a = 1x and b = 1y in the system of equations:
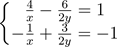 , find the solution set (x,y).
, find the solution set (x,y).
View Ans
(b) Let U be a universal set and A and B be the subsets of U where:
U = {1,2,3,4,5,6,7,8,9,10}, A = {odd numbers} and B = {prime numbers} (i) Represent this information in a venn diagram.
(ii) Find A n B? and (A U B) ?
View Ans
4. (a) Given vectors a = 6i + 12j, b = 17i + 18j :
(i) Find the vector c = 2a – b and its magnitude correctly to 3 significant figures. (ii) Represent vector c in part (a)(i) on the x - y plane.
View Ans
(b) Find the equation of the line passing passing through the midpoint of the points A(− 3 2, ) and B(1,− )4 and which is perpendicular to line AB .
View Ans
5. (a) In triangle ABC , X , Y and Z are the midpoints of sides AB , AC and BC respectively. If
ZX = ZY and ZXBˆ = ZY Cˆ = 90°;
(i) Represent this information diagrammatically, (ii) Show that ABZˆ = ACZˆ .
View Ans
(b) The areas of two similar polygons are 27 and 48 square metres. If the length of one side of the smaller polygon is 4.5 cm, find the length of the corresponding side of the larger polygon.
View Ans
6. (a) The number of tablets given to a patient was found to be directly proportional to the weight of the patient. If a patient with 36 kg was given 9 tablets, find how many tablets would be given to a patient whose weight is 48 kg.
View Ans
(b) Four people can eat 2 bags of rice each weighing 10 kg in 12 days. How many people can eat 6 bags of rice of the same weight in 18 days?
View Ans
7. (a) Mariam, Selina and Moses contributed 800,000, 1,200,000 and 850,000 shillings respectively while starting their business.
(i) Find the ratio of their contributions in simplest form.
(ii) If the business made a profit of 1,900,000 shillings; find how much each got if the profit was shared in the same ratio as their contributions.
View Ans
(b) A dealer bought 10 books for 200,000. He sold 25 of them at 30,000 shillings each and the remaining at 25,000 shillings each. What was his percentage profit?
View Ans
8. (a) The 8times the 2th term of an arithmetic progression is 9 greater than the 5 nd term. Find the common difference and the first term of the arithmetic progression. th term and the 10 th term is 10
View Ans
(b) The sum of the first two terms of a geometric progression is 18 whereas the sum of the second and third term is 54, find the first term and the common ratio.
View Ans
9. (a) A river with parallel banks is 20 m wide. If P and Q are two points on either side of the river, as shown in the figure below, find the distance PQ.

View Ans
(b) In the triangle LMN , LM = 5m, LN = 6m and angle MLN = 66°. Find MN .
View Ans
10. (a) If one of the roots of the quadratic equation x2 + bx + 24 = 0 is 112 , find the value of b.
View Ans
(b) Two numbers differ by 3. If the sum of their reciprocals is 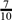 , find the numbers.
, find the numbers.
View Ans
SECTION B (40 Marks)
Answer four (4) questions from this section.
11. A shopkeeper sells refrigerators and washing machines. Each refrigerator takes up 1.8 m 2 of space and costs 500,000 2 of space and costs 300,000 shillings; whereas each washing machine takes up 1.5 mshillings. The owner of the shop has 6,000,000 shillings to spend and has 27 m 2 of space.
(a) Write down all the inequalities which represent the given information.
(b) If he makes a profit of 30,000 shillings on each refrigerator and 40,000 shillings on each washing machine, find how many refrigerators and washing machines he should sell for maximum profit.
View Ans
12. The following were the scores of 35 students in a mathematics mock examination:
07, 19, 78, 53, 43, 67, 12, 54, 27, 22, 33, 80, 25, 58, 50, 36, 65, 33, 16, 19, 34, 20, 55, 27, 37, 41, 04, 32, 48, 28, 70, 31, 61, 08, 35
(a) Prepare the frequency distribution table using the class intervals: 0–9, 10–19, 20–29, etc.
(b) Which class interval has more students?
(c) Represent the information in a histogram and a frequency polygon and then find the mode.
(d) Calculate the median mark.
View Ans
13. (a) In the figure below, BD is a tangent to the circle having the centre O .
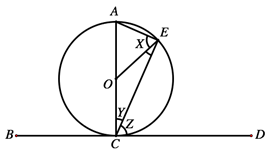
Given that angle OEC = 28°, find the values of angles marked X , Y and Z .
View Ans
Given that angle OEC = 28°, find the values of angles marked X , Y and Z .
(b) Calculate the distance from Chagwe (5°S, 39°E) to Minga (12°S, 39°E) in kilometres. Use π = 3.14, the radius of the earth R = 6370km and write the answer correct to 1 decimal place.
View Ans
(c) If a bus leaves Chagwe at 8:00 am on Monday and travels at 40 km/hour, at what time will it reach Minga?
View Ans
14. (a) Given:
Opening stock 01-01-2012 34,430/=
Closing stock 31-12-2012 26,720/=
Net purchases during 2012 212,290/=
Expenses for the year 45,880/=
Gross Profit is 50% of cost of goods sold
Find: (i) Cost of goods sold (ii) The gross profit
View Ans
(b) On 1 st June, 2013 Mrs. Lemisha started business with capital of 100,000/= and mad ehte following transactions
June 2 bought furniture 40,000/=
7 bought goods 70,000/=
11 sold goods 65,000/=
16 paid Sundry expenses 30,000/=
19 cash sales 80,000/=
24 paid wages 50,000/=
26 withdraw cash 30,000/=
(i) Prepare the cash account
View Ans
(ii) Prepare the balance sheet as at 30/06/2013
View Ans
(iii) Explain the importance of the balance sheet you have prepared in part (b)(ii) above.
View Ans
15. (a) Given matrices 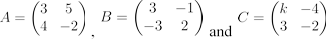 :
:
(i) Find A2 + 2A
View Ans
(ii) Find and t y such that B2 = tB + yI where is an identity matrix.I
View Ans
(iii) Find the value of k if the determinant of C is 5.
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256