THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Tuesday, 03rdNovember 2015 a.m.
Instructions
1. This paper consists of sections A and B.
2. Answer all questions in sections A and four (4) questions from section B. Each question in section A carries 6 marks while each question in section B carries 10 marks.
3. All necessary working and answers for each question done must be shown clearly.
4. Mathematical tables may be used.
5. Calculators and cellular phones are not allowed in the examination room.
6. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) If p = 6.4 × 104 and q = 3.2 × 105 , find the values of:
(i) p × q ,
(ii) p + q .
Write the answers in standard form.
View Ans
1.(b) Evaluate
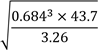
Using mathematical tables and write the answer correctly to 3 significant figures
View Ans
2. (a) Solve for x in the equation 4-2x × 82 = 4 × 16x .
View Ans
(b) Find the value of log900 given that log3 = 0.4771 .
View Ans
3.(a) Find the solution set of the inequality
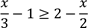
and indicate it on a number line
View Ans
(b) The Venn diagram below shows the universal set U and its two subsets A and B.
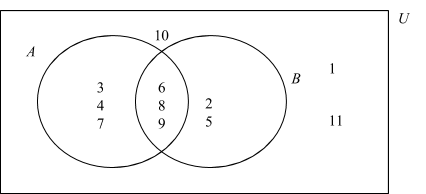
Write down the elements of:
(i) A'
(ii) B',
(iii) A UB ,
(iv) A'U B'.
View Ans
(c) Verify that n(A U B) = n(A) + n(B) - n(A n B) where A and B are the sets given in part 3(b).
View Ans
4. (a) Given vectors (i) the vector a = 3i + 2 j , b = 8i + 3j and c = 2i + 4 j find:
(i) d=3a -b +1/2c (ii) a unit vector in the direction of d.
View Ans
(b) Find the equation of the line passing at point (6, 2) and it is perpendicular to the line that crosses the x-axis at 3 and the y-axis at 4.
View Ans
5. (a) Two triangles are similar. A side of one triangle is 10 cm long while the length of the corresponding side of the other triangle is 18 cm. If the given sides are the bases of the triangles and the area of the smaller triangle is 40 cm2 , find the area and the height of the larger triangle.
View Ans
(b) In the figure below CB = BD = DA and angle ACD = x .
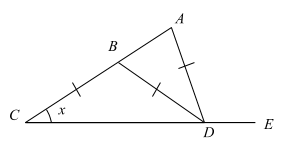
(i) Show that angle ADE = 3x ,
(ii) Calculate the measure of angle CDA if x = 39°.
View Ans
6. (a) The variable v varies directly as the square of x and inversely as y. Find v when x = 5 and y = 2 ? given that when v = 18 and x = 3 the value of y = 4 .
View Ans
(b) The temperature (Ti) inside a house is directly proportional to the temperature (To) outside the house and is inversely proportional to the thickness (t) of the house wall. If Ti = 32°C when To = 24°C and t = 9cm , find the value of t when Ti = 36°C and To = 18°C
View Ans
7. (a) A shopkeeper makes a 20% profit by selling a radio for sh. 480,000.
(i) Find the ratio of the buying price to the selling price.
(ii) If the radio would be sold at 360,000, what would be the percentage loss?
View Ans
(b) A farmer sold a quarter of his maize harvest and gave one third of the remaining to his relatives. If the farmer remained with 25 bags of maize find how many bags of maize did the farmer harvest.
View Ans
8. (a) How many terms of the series 3 + 6 + 9 + 12 + ... are needed for the sum to be 630?
View Ans
(b) Jennifer saved sh. 6 million in a Savings Bank whose interest rate was 10% compounded annually. Find the amount in Jennifer’s savings account after 5 years.
View Ans
9.(a) Find value of
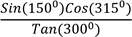
Without using mathematical tables
View Ans
(b) Calculate the angles of a triangle which has sides 4m, 5m and 7m.
View Ans
10. (a) Factorize completely 2x2 + x - 10 by splitting the middle term.
View Ans
10(b) Solve the equation
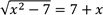
View Ans
SECTION B (40 Marks)
Answer four (4) questions from this section.
11. A small industry makes two types of clothes namely type A and type B. Each type A takes 3 hours to produce and uses 6 metres of material and each type B takes 6 hours to produce and uses 7 metres of material. The workers can work for a total of 60 hours and there is 90 metres of material available. If the profit on a type A cloth is 4,000 shillings and on a type B is 6,000 shillings, find how many of each type should be made for maximum profit.
View Ans
12. The following marks were obtained by 32 students in a physics examination:
32, 35, 42, 50, 46, 29, 39, 38, 45, 37, 48, 52, 37, 58, 52, 48, 36, 54, 37, 42, 64, 37, 34, 28, 58, 64, 34, 57, 54, 62, 48, 67.
(a) Prepare a frequency distribution table using the class intervals: 24 29, 30 35 etc.
(b) Draw the histogram.
(c) Draw the cumulative frequency curve and use it to estimate the median.
(d) Find the mean mark.
View Ans
13. (a) Find the value of the angles a and b in the figure below.
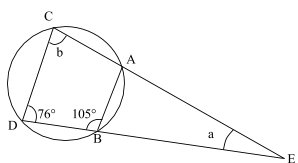
View Ans
(b) A rectangular box with top WXY Z and base ABCD has
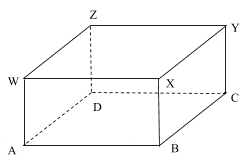
AB = 9cm, BC = 12cm and WA = 3cm.
Calculate:
(i) The length of AC ,
(ii) The angle between WC and AC .
View Ans
(c) Two places P and Q both on the parallel of latitude 26°N differ in longitude by 40°. Find the distance between them along their parallel of latitude.
View Ans
14. The following trial balance was extracted from the businessman books’ of Chericho Ramaji, at
31st December 2006.
| S/N | Details | Dr. (T.Sh) | Cr.(Tshs.) |
| 1. | Capital |
| 830,000 |
| 2. | Purchases | 1,200,000 |
|
| 3. | Sales |
| 1,750,000 |
| 4. | Return inwards | 55,000 |
|
| 5. | Return outwards |
| 64,000 |
| 6. | Plant and machine | 240,000 |
|
| 7. | Furniture and fittings | 75,000 |
|
| 8. | Sundry debtors | 137,000 |
|
| 9. | Sundry creditors |
| 86,000 |
| 10. | Wages | 228,000 |
|
| 11. | Bad debts | 36,000 |
|
| 12. | Discount received |
| 27,000 |
| 13. | Opening stock | 500,000 |
|
| 14. | Insurance | 16,000 |
|
| 15. | Commission receivable |
| 43,000 |
| 16. | Trade expenses | 22,000 |
|
| 17. | Cash in hand | 17,000 |
|
| 18. | Cash at bank | 274,000 |
|
|
| Total | 2,800,000 | 2,800,000 |
Prepare Trading, Profit and Loss account for the year ended 31st December 2006.
View Ans
15.(a) Given matrices
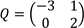
And
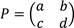
Such that
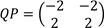
Find elements of matrix P
View Ans
(b) Determine the matix A from the equation
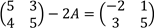
View Ans
(c) Given a triangle with vertices A(0,0) , B(3,0) and C(3,1) ? find its image under:
(i) a translation by the vector (2,3),
(ii) the enlargement matrix 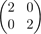
(d) Sketch the triangle and the images in parts (c)(i) and (ii) on the same pair of axes and comment on their sizes.
View Ans
16. (a) The function f is defined as follows:
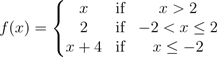
(i) Sketch the graph of f(x),
(ii) Determine the domain and range of f(x) .
View Ans
(b) Jeremia has two shirts, a white one and a blue one. He also has 3 trousers, a black, green and a yellow one. What is the probability of Jeremia putting on a white shirt and a black trouser?
View Ans
(c) If a number is to be chosen at random from the integers 1, 2, 3, ..., 11, 12. find the probability that:
(i) It is an even number,
(ii) It is divisible by 3.
View Ans
(d) If in part 16(c) above, E1 is the set of even numbers and E2 the set of numbers that are divisible by 3, show whether E1 and E2 are mutually exclusive events.
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256