THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Tuesday, 04 th November 2014 p.m.
Instructions
1. This paper consists of sections A and B.
2. Answer all questions in sections A and four (4) questions from section B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks..
3. All necessary working and answers for each question must be shown clearly.
4. Mathematical tables may be used.
5. Calculators and cellular phones are not allowed in the examination room.
6. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) Kisiki and Jembe are riding on a circular path. Kisiki completes a round in 24 minutes whereas Jembe completes a round in 36 minutes. If they both started at the same place and time and go in the same direction, after how many minutes will they meet again at the starting point?
View Ans
(b) An empty bottle weighs 115 grams. If 45 tablets each weighing  gram are put in the bottle, what is the total weight?
gram are put in the bottle, what is the total weight?
View Ans
2. (a) (i) Express (√3 + 5)2 in the form a + b√3, where a and b are integers.
(ii) Express
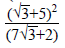
in the form p + q√3, where p and q are rational numbers.
View Ans
(b)  Solve for x if (811)−6x × 81 = √9 .
Solve for x if (811)−6x × 81 = √9 .
View Ans
3. (a) The Venn diagram below shows the number of elements in sets P and Q.
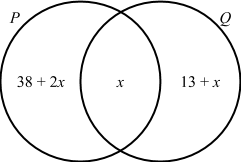
If n(P U Q) = 95, calculate:
(i) The value of x,
(ii) n(P n Q)′.
View Ans
(b) The age of Timothy is 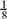 the age of his father. If the sum of their ages is 54 years, find the age of the father.
the age of his father. If the sum of their ages is 54 years, find the age of the father.
View Ans
4. (a) Find the equation of the line passing through (6,4) and perpendicular to the line whose equation is 12x + 6y = 9.
View Ans
(b) If a = 2 i + 3 j, b = 19i – 15j and c = 5i – 7j, find the value of x such that xa + yc =b.
View Ans
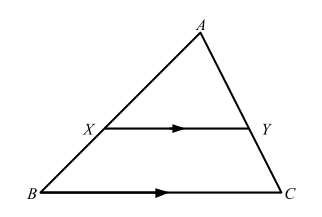
5.(a) Given that XY = 2cm, BC = 3cm and area of XYCB = 10cm3 , calculate the area of triangle AXY .
View Ans
(b) Determine the length of one side of a regular quadrilateral inscribed in a circle of radius 10cm.
View Ans
6. (a) Juma sells one litre of milk at sh 600. How many litres of milk will Juma sell to get sh 208,800?
View Ans
(b) The compression l of a spring is directly proportional to the thrust, T newtons exerted on it. If a thrust of 2 newtons produces a compression of 0.4cm, find:
(i) The compression when the thrust is 5 newtons,
(ii) The thrust when the compression is 0.7cm.
View Ans
7. (a) Kieku has to share 80 books with his younger sisters Upendo and Okuli. He decided that for every 2 books that Okuli gets, Upendo gets 3 and he gets 5 books. Find the number of books each gets.
View Ans
(b) Nyaumwa invested a certain amount of money in a bank which pays interest rate of 6 percent after every 6 months. After 5 years, his total savings were sh 9,600,000. Determine the amount of money Nyaumwa invested initially.
View Ans
8. (a) The 20th term of an arithmetic progression is 60 and the 16th term is 20. Find the sum of the first 40 terms.
View Ans
(b) A shopkeeper invested sh 4,800,000 for 5 years. If the amount of money accumulated is sh 7,730,450, calculate the compound interest rate.
View Ans
9. (a) Find the length marked y in four significant figures, given that DC=20cm.
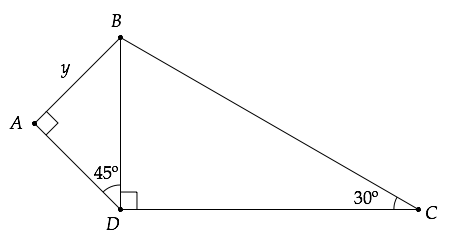
View Ans
(b) A 4m ladder rests against a vertical wall with its foot 2m from the wall. How far up the wall does the ladder reach? Give your answer in two decimal places.
View Ans
10. (a) Use the quadratic formula to solve x2 + 4x − 12 = 0
View Ans
(b) A garden measuring 12 by 16 metres is to have a pedestrian pathway of equal width constructed all around it, increasing the total area to 285 square metres. What will be the width of the pathway?
View Ans
SECTION B (40 Marks)
Answer four (4) questions from this section.
11. A farmer has 20 hectares for growing tomatoes and cabbages. The cost per hectare for tomatoes is sh 48,000 and for cabbages is sh 32,000. The farmer has budgeted sh 768,000. Tomatoes require one manday per hectare and cabbages require two mandays per hectare. There are 36 mandays available. The profit on tomatoes is sh 160,000 per hectare and on cabbages is sh 192,000 per hectare. Find the number of hectares of each crop the farmer should plant to maximize the profit.
View Ans
12. The heights of some plants grown in a laboratory were recorded after 5 weeks. The results are shown in the following table:
| Height (cm) | 11 - 15 | 16 - 20 | 21 - 25 | 26 - 30 | 31 - 35 | 36 - 40 |
| Frequency | 4 | 8 | 20 | 21 | 12 | 3 |
(a) Calculate the mean and mode.
(b) Draw a cumulative frequency curve for the data.
(c) Estimate the median from the graph.
View Ans
13.(a) Prove that the sizes of the angles in the same segment of a circle are equal.
View Ans
(b) In the figure below, O is the centre of the circle and AD bisects angle BAC . Find angle BCD.
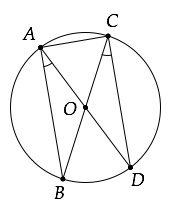
View Ans
(c) Kicheko and Mtakuja are two villages on latitude 60°S. The distance between Kicheko and Mtakuja measured along the parallel of latitude is 1111km. Find the difference between their longitudes in two significant figures.
View Ans
14. Mr. Kijembe started business on 16th March, 2011 with capital in cash 2,066,000/=
March 17 bought goods for Cash 1,000,000/=
19 bought shelves for Cash 1,100,000/=
20 sold goods for Cash 900,000/=
21 purchases for Cash 800,000/=
22 sold for Cash 1,400,000/= 26 paid Rent 300,000/=
Record the above transactions in a cash account ledger and extract a trial balance. State two uses of the trial balance you have prepared.
View Ans
15. (a) (i) Determine a matrix M which represents a reflection in the line y − x = 0
(ii) Find the image of the line x + 2y − 4 = 0 after a reflection in the line y − x = 0.
View Ans
(b) (i) If
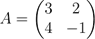
find |A| and A−1.
(ii) Use the inverse matrix obtained in (b)(i) to solve 3x + 2y = 12 and 4x − y = 5.
View Ans
16. (a) A bag contains 6 white balls and 3 yellow balls. A ball is selected at random and not replaced.
Another ball is then selected. Find the probability of selecting one white ball and one yellow ball.
View Ans
(b) Given
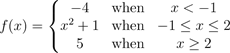
(i) Sketch the graph of f(x).
(ii) State the domain and range of f(x) .
(iii) Is f(x) a one-to-one function? Give reason(s).
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256