THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For School Candidates Only)
Time: 3 Hours Tuesday, 05thNovember 2013 a.m.
Instructions
1. This paper consists of sections A and B.
2. Answer all questions in section A and four (4) questions from section B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
3. All necessary working and answers for each question attempted must be shown clearly.
4. Mathematical tables may be used.
5. The following constants may be used:
(a) The radius of the earth R = 6370km
(b) π = 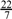
6. Calculators and cellular phones are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) A shopkeeper sold 292 t-shirts at the price of sh. 6950. Estimate how much money she got.
View Ans
(b) Express 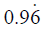 in the form of a/b where a and b are integers such that b =/ 0 .
in the form of a/b where a and b are integers such that b =/ 0 .
View Ans
2. (a) If logy + 2log(3x + 1) = 1, express y in terms of x .
View Ans
(b) Simplify 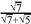 by rationalizing the denominator.
by rationalizing the denominator.
View Ans
3. (a) If m * n = m + 4n, find x given that 3 * (x * 1) = 27.
View Ans
(b) There are 48 men at a meeting of whom 24 are teachers, 36 are parents and 16 are both teachers and parents. By using a Venn diagram, find the number of men who are neither teachers nor parents.
View Ans
4. (a) Find the direction cosines of C = 9i + 12j, hence show that the sum of the squares of these direction cosines is one.
View Ans
(b) Find the equation of the line through the points (4,6) and the midpoint of (2,4) and (10,4).
View Ans
5. (a) The length of two sides of a triangle are 16cm and 20cm. Find the area of the triangle if the included angle is 30° .
View Ans
(b) In the figure below, calculate the length BD:
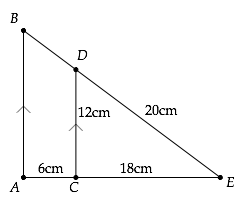
View Ans
6. (a) A bus travels 240km using 16 litres of diesel. How many litres of diesel are needed to drive 90km?
View Ans
(b) If y2 varies directly to x − 1 and inversely to x + d and if x = 2 , d = 4 for y = 1, then find x when y = 2 and d = 1.
View Ans
7. (a) A radio is bought for sh 400,000 and sold for sh 500,000. Find:
(i) The profit made
(ii) The percentage profit.
View Ans
(b) Find the time in which sh 300,000 will earn an interest of sh 60,000 if the interest rate is 10% per annum.
View Ans
8. (a) The first term of an arithmetic progression is 12 and the common difference is 10. Find the nth term.
View Ans
(b) Find the amount of money accumulated at the end of 2 years after investing 500,000 shillings at a compound interest rate of 10% annually.
View Ans
9. (a) A ladder leans against a wall. If the ladder reaches 12m up the wall and its foot is 9m from the base of the wall, find the length of the ladder.
View Ans
(b) Given that A and B are complementary angles and sinA = 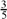 , find tanB (Leave your answer as an improper fraction).
, find tanB (Leave your answer as an improper fraction).
View Ans
10. (a) What must be added to x2 + 8x to make the expression a perfect square?
View Ans
(b) Find two consecutive odd numbers whose product is 195.
View Ans
SECTION B (40 Marks)
Answer any four (4) questions from this section.
11. (a) Solve by graphical method the following system of simultaneous equations:
4x + y = 6
5x + 2y = 9
(b) A farm is to be planted with sorghum and maize while observing the following constraints:
| Sorghum | Maize | Maximum total |
| Days labour per hectare | 4 | 2 | 20 |
| Labour cost per hectare | 1400 | 1200 | 8400 |
| Cost of fertilizer per hectare (shs) | 600 | 800 | 4800 |
If sorghum yields a profit of 800,000 shillings per hectare while maize yields 600,000 shillings per hectare, how many hectares should be planted with each crop for maximum profit?
View Ans
12. Carefully study the frequency distribution table which shows the marks of 100 students in a Physics examination.
| Marks | 41 - 50 | 51 - 60 | 61 - 70 | 71 - 80 | 81 - 90 | 91 - 100 |
| Number of Students | 10 | 22 | 34 | 25 | 7 | 2 |
Calculate
(a) the mean given the assumed mean is 75.5,
(b) the median in two decimal places,
(c) the mode in two decimal places.
View Ans
13. (a) The figure below shows a rectangular prism in which AB = 10cm , BC = 8cm and Calculate the length of DF (Leave your answer in surd form)
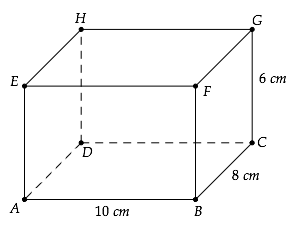
View Ans
(b) If O is the centre of a circle given below, find the value of x.
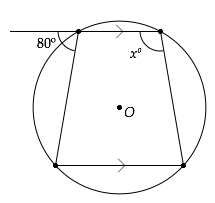
View Ans
(c) Calculate the circumference of a small circle, in kilometres, along the parallel of latitude 30°N (Leave your answer in surd form).
View Ans
14. Mr. Chapakazi commenced business on 1st June, 2011 with capital in cash 5,500,000/=
June 2 Bought goods by Cash 2,000,000/=
3 Bought furniture for Cash 600,000/=
7 Sold goods for Cash 2,000,000/=
11 Cash purchases 700,000/=
13 Paid Rent for Cash 2,000,000/=
16 Cash Sales 950,000/=
20 Paid Transport for Cash 80,000/=
22 Sold goods for cash 250,000/=
26 Paid salaries for Cash 160,000=
Record the above transactions in the cash account, balance them and extract the Trial Balance.
View Ans
15. (a) Given
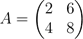
find A−1.
(b) Use the results obtained in part (a) to find the point of intersection of the following system of simultaneous equations:
2x + 6y = 22
4x + 8y = 32
(c) Find the image of the point obtained in part (b) above under a rotation 90° anticlockwise.
View Ans
16. (a) A die and a coin are tossed together. What is the probability of getting a tail and an even number?
View Ans
(b) Draw the graph of the inverse of R = {(x,y) : y ≥ 0 and y ≤ x}. Find its domain and range.
View Ans
(c) Without using a table of values, draw the graph of y = x2 − 4x + 2 and use it to solve the equation x2 − 4x = 5.
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256