THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For School Candidates Only)
Time: 3 Hours Monday, 4th October 2010 a.m.
Instructions
1. This paper consists of sections A and B.
2. Answer all questions in section A and four (4) questions from section B.
3. All necessary working and answers for each question done must be shown clearly.
4. Mathematical tables may be used unless otherwise stated.
5. Calculators and cellular phones are not allowed in the examination room.
8. You are advised to spend not more than two (2) hours on section A and the remaining time on section B.
9. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section showing all necessary working and answers.
1. (a) Write 624.3278 correct to:
- five (5) significant figures
- three (3) decimal places.
View Ans
(b) A mathematics teacher bought 40 expensive calculators at shs.16,400 each
and a number of other cheaper calculators costing shs.5,900 each. She spent a total of shs. 774,000. How many of the cheaper calculators did she buy? (6 marks)
View Ans
2. (a) Evaluate without using mathematical tables 2 log 5 + log 36 — log 9.
View Ans
(b) Simplify
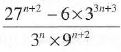 (6 marks)
(6 marks)
View Ans
3. (a) Given that A= {x : 0 ≤ x ≤8}
B = {x : 3 ≤ x ≤8}
where x is an integer, in the same form, represent in a Venn diagram
- A u B
- A n B
and hence find the elements in each set.
View Ans
(b) In a school of 75 pupils, 42% of the pupils take Biology but= not Chemistry, 32% take both subjects and 10% of them take Chemistry but not Biology. How many pupils do not take either Biology or Chemistry? (6 marks)
View Ans
4. (a) (i) Without using mathematical tables, find the numerical value of
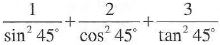
(ii) Write down the equation of the line which passes through (7, 3) and which is inclined at 45° to the positive direction of the x-axis.
View Ans
(b) The position vectors of the points A, B and C are 4i - 3j , i +3j and -5i + j respectively. Find the vectors AB, BC and AC hence verify that AB + BC = AC (6 marks)
View Ans
5. (a) The volume of two similar cylinders is 125 cm3 and 512 cm3. If the radius of the larger cylinder is 8cm, find the radius of the smaller cylinder.
View Ans
(b) In the diagram below, show that
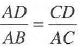
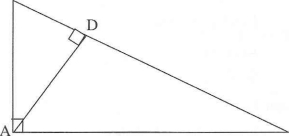 (6 marks)
(6 marks)
View Ans
6. (a) Juma bought motor vehicle spare parts from Japan worth 5,900,000 Japanese Yen. When he arrived in Tanzania he was charged custom duty of 25% on the spare parts. If the exchange rates were as follows:
1 US dollar = 118 Japanese Yen
1 US dollar = 76 Tanzania Shillings
Calculate the duty he paid in Tanzania shillings.
View Ans
(b) The distance of the horizon d km varies as the square root of the height h m of the observer above sea level. An observer at a height of 100m above sea level sees the horizon at a distance of 35.7 km.
Find
(i) the distance of the horizon from an observer 70m above sea level.
(ii) an equation connecting d and h. (6 marks)
View Ans
7. (a) An amount of Tshs. 12,000 is to be shared among Ali, Anna and Juma in the ratio 2:3:5 respectively. How much will each get?
View Ans
(b) A certain worker used his salary as follows: 20% on house rent, 45% on food, 10% on refreshment and 15% on school fees. If he/she was left with Tsh.22,000, determine:
- The salary of this worker.
- The amount of money which he/she spent on food. (6 marks)
View Ans
8. (a) Find the general term and hence the 30th term of the sequence
1, -2, 4, -8, ......
View Ans
(b) Given the series 100 + 92 + 84 +.....
Find
- the 20th term
- the sum of the first 20 terms. (6 marks)
View Ans
9. (a) If tan A = ¾ and A is acute, find cos A, sin A and hence verify the identity cos2 A + sin2 A =1
View Ans
(b)
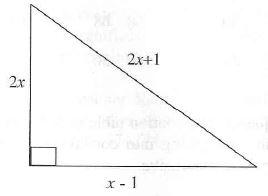
Given the right angled triangle above whose sides are measured in centimeter determine:
- the value of x
- the area of the triangle (6 marks)
View Ans
10. (a) Factorize each of the following expressions:
- 3a2c -5a 2d - 3b2 c + 5b2d
- 3(2 - y2)-17y
(b) Find the value of y which satisfies the equation 3(2 - y2) - 17y = 0 (6 marks)
View Ans
SECTION B ( 40 Marks)
Answer four (4) questions from this section. Extra questions will not be marked.
11. (a) Maximize f = 2y — x subject to the following constraints:
x ≥ 0
y ≥ 0
2x+y ≤ 6
x+2y ≤ 6
(b) Sara had 300 shillings to buy erasers and pencils. An eraser cost 20 shillings while a pencil costs 30 shillings. If the number of erasers bought is at least twice the number of pencils, formulate the inequalities that represent this information. (10 marks)
View Ans
12. The data below represent masses in kg of 36 men.
| 51 | 61 | 60 | 70 | 75 | 71 | 75 | 70 | 74 | 73 | 72 | 82 |
| 70 | 71 | 76 | 74 | 50 | 68 | 68 | 66 | 65 | 72 | 69 | 64 |
| 83 | 63 | 83 | 58 | 80 | 90 | 50 | 89 | 55 | 62 | 62 | 61 |
- Prepare a frequency distribution table of class interval of size 5 beginning with the number 50 taking into consideration that both lower limit and upper class limits are inclusive.
- Calculate the mean and mode from the frequency distribution table prepared in (i) above by using assumed mean from the class mark of the modal class. (10 marks)
View Ans
13. (a) Below is a circle with centre 0 and radius r units. By considering the circumference of the circle, the area of the circle, the given angle 0 and the degree measures of a circle (3600), develop the formula for finding:
- arc length AB
- area of sector AOB.
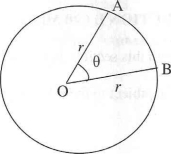
(b) Find (i) the length of arc AB
(ii) the area of the sector
If θ=570 and r=5.4cm (Use π =22/7)
View Ans
14. From 1st January to 29th January 2006 Mr. Bin decided to keep records of his business as follows:
| Jan. 1 | Mr. Bin started a business with capital in cash | 500,000.00 |
| 5 | Purchased goods | 254,000.00 |
| 6 | Sold goods | 290,000.00 |
| 9 | Purchased goods | 204,000.00 |
| 10 | Expenses | 24,000.00 |
| 29 | Sold goods | 320,000.00 |
You are required to:
- prepare the trial balance
- open capital and cash account.
N.B All payments and receipts were made in cash. (10 marks)
View Ans
15. (a) A transformation T has the matrix
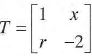
Under the same transformation T, the point (-4, 1) is mapped onto the point (6, 3). Find x and r.
View Ans
(b) For what values of n will the matrix
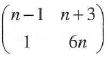
be non-singular? (10 marks)
View Ans
16. (a) If f (x) = -2x + 3 find f -1 (3)
View Ans
(b) Draw the graph of f (x) = | x —1| for -4 ≤ x ≤ 4
(c) State the domain and range of f (x)=|x-1|
View Ans
(d) The probability that Rose and Juma will be selected for A - level studies after completing their O- level studies are 0.4 and 0.7 respectively. Calculate the probability that:
- both of them will be selected.
- either Rose or Juma will be selected. (10 marks)
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256