THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL
FORM TWO SECONDARY EDUCATION EXAMINATION, 2011
0041 BASIC MATHEMATICS
Time: 2 ½ Hours
INSTRUCTIONS
1. This paper consists of sections A and B.
2. Answer ALL questions showing clearly all the working and answers in the space provided.
3. ALL writing must be in blue or black ink EXCEPT drawings which must be in pencil.
4. Write your examination number at the top right corner of every page.
5. Mathematical tables, geometrical instruments and graph papers may be used where necessary.
6. Cell phones and calculators are not allowed in the examination room.
SECTION A (60 MARKS)
1. Add the first three common multiples of 3 and 5.
View Ans
2. Two numbers are such that the first number plus the second number is 7. The first number minus twice the second number is 1. Find the numbers.
View Ans
3. Re-arrange the following fractions starting from the greatest to the smallest:
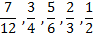
View Ans
4. In Mpitimbi village 70% of 1200 cows are black and 22.3% of 18000 goats are white. Find the sum of black cows and white goats.
View Ans
5. Juma walked a distance of 1 kilometre and 300 metres from his home to a shop. He then walked further 0.85 kilometres to the stadium to greet his friend who was watching football. Calculate the total distance in metres Juma travelled.
View Ans
6. Express 0.007678 to 3 significant figures
View Ans
.7. Find the value of X in the following figure, given that m(BAC) = 50° and m(ABC) = 75°
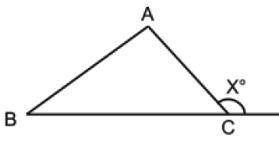
View Ans
8. Simplify 3a – 5b – 7a + 6c + 7a + 8b
View Ans
9. Expand the expression (3m + 7n) 2
View Ans
10. Find two positive numbers whose difference is 5 and whose product is 266.
View Ans
11. George and Asha shared 35 mangoes in the ratio 2:3. How many mangoes did each get?
View Ans
12. Find the slope of the line with equation 7x + 2y = 8.
View Ans
13. A school assembly ground is 30m by 30m. Part of the ground is a concrete rectangle of 25m by 5m, while the rest is grass. Calculate the area of the grass.
View Ans
14. Rationalize the denominator to the simplest form:
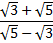
View Ans
15. Simplify (-4g5)3
View Ans
16. A mother is 4 times older than her child. Five years ago the product of their ages was 175. Find their present ages.
View Ans
17. Show that logmn=loga m + logan
View Ans
18. Given that m(BAC) = 80°, m(BCA) = 69°, m(YXZ) = 31° and m(YZX) = 80°. Show that the following triangles are similar.
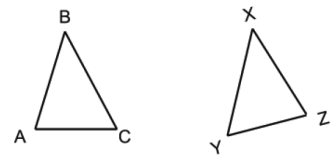
View Ans
19. The co-ordinates of the square PQRS are given by P(1, 4), Q(3, 4), R(3, 2), and S(1, 2). Write the co-ordinates of the image of the square P’Q’R’S’ under reflection in the x-axis.
View Ans
20. Which of the following triples fits to Pythagoras theorem?
(a) (33, 56, 65)
(b) (15, 30, 35)
View Ans
SECTION B (40 Marks)
21. Given that the universal set ξ = {all counting numbers less than 29}. M and N are the subsets of set ξ where M = {Numbers which are multiples of 4} and N = {Numbers which are perfect
squares}. Find (M∩N).
View Ans
22. An engineer finds that the angle of elevation of the top of a building from a point on the ground is 25°. She walks along a straight line 30 metres closer to the foot of the building and finds that the angle of elevation is 50°. Determine the height of the building. (Your answer should be correct to one decimal place)
View Ans
23. The masses of 40 students from the University of Dar es Salaam were recorded to the nearest kilogram as follows:
| 60 | 64 | 63 | 67 | 66 | 68 | 59 | 58 | 59 | 60 |
| 64 | 66 | 65 | 60 | 73 | 70 | 63 | 69 | 70 | 60 |
| 66 | 70 | 74 | 69 | 63 | 69 | 59 | 65 | 64 | 65 |
| 73 | 61 | 62 | 64 | 61 | 61 | 62 | 63 | 58 | 73 |
From the data given, construct a frequency distribution table taking equal class intervals 57 - 61, 62 -66, 67 - 71, … and determine the class interval with the highest frequency.
View Ans
24. Use mathematical tables to compute
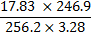
correct to decimal places.
View Ans
25. Calculate MN and YM in the following figure
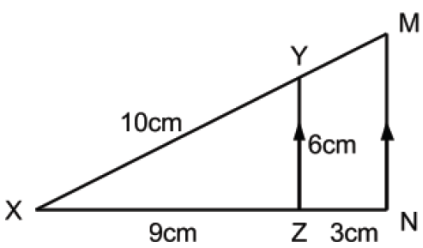
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256