PRESIDENT’S OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
SECONDARY SCHOOL EXAMINATION SERIES
MATHEMATICS FORM TWO
PRE-NECTA – 2025
041
Time: 2:30 Hours AUG, 2025
INSTRUCTIONS
1. This paper consists of a total ten (10) compulsory questions
2. Show your work clearly
3. All writing must be in blue or black ink, except drawings which should be in pencil
4. All communication devices, programmable calculators and any unauthorized materials are not allowed in the examination room
1 a) The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 10 seconds respectively. If they change simultaneously at 7a.m at what will they change simultaneously again?
b) If x = 0.567567567... and y – 0.83 by converting these decimals to
fractions, find the exact value of ![]() in simplest form
in simplest form
2 a) If T= 
Find the value of t
b) Write ‘’L’’ in terms of M, N and T from the formula =

c) Determine the value of x if log5(x+1)-1=log5(x-3)
3. a) A lorry carries 7.2 tonnes of sand from the mining area to the industrial site. One the way 230kg of sand either fall off or blow away. What mass of sand will remain by the end of the journey? Give the answer in tonnes b) An article was sold for sh 160,000 at a profit of 25% find the buying price
of the article
4. a) Solve for the quadratic X2 – 8x +7 = 0
b) Solve for x and y if;

5. a) The sum of two numbers is 127. If the difference/ between numbers is 7, find the numbers.
b) If : = 2:3 π : = 5:6 find : π :: 6.
6. a) Rationalize the denominator and simplify:
b) Find the area of an equilateral triangle whose sides are 20cm
7. a) A certain amount of money was divided in the ratio 2:3:5. If the difference between the largest share and the smallest share was sh 7,500/=, find the largest share
b) Find the x – intercept of a line through points (-3,5) and (0, -1)
8. a) The scale of map is 1cm to 10km. find the distance on the map between two towns which are:
(a) 20 km apart (b) 48.5 km apart
9. a) Use the following figure to find the values of x and y

b) Find the value of each of the following expressions and simplify the
answers

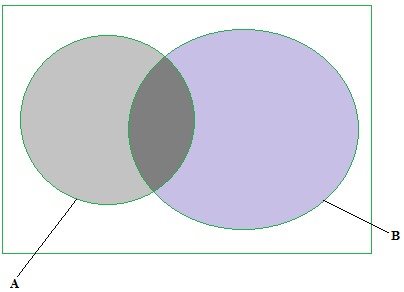
10. In a class of 45 pupils, 25 takes History, 27 takes Commerce. If the total number of those who takes History and Commerce is 37, find:
a) The number of pupils who takes both History and Commerce
b) The number of pupils who takes History only
c) The number of pupils who takes neither History nor Commerce
FORM TWO MATHEMATICS EXAM SERIES 215
FORM TWO MATHEMATICS EXAM SERIES 215

FORM TWO MATHEMATICS EXAM SERIES 206
FORM TWO MATHEMATICS EXAM SERIES 206
Candidate’s index number ……………………………….
THE PRESIDENT'S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION
FORM TWO MID TERM EXAMINATION MAY, 2025
041 BASIC MATHEMATICS
TIME : 2: 30HOURS
INSTRUCTIONS.
1. This paper consists of ten ( 10 ) questions
2. Answer ALL questions in the space provided
3. Show clearly all necessary working
4. Where necessary mathematical table may be used.
5. Cellular phones, calculator and any un- authorized materials are not allowed in the examination room
6. Write the index number at the top right corner of every page.
1. a) Four wooden rods are of lengths 120cm, 150cm, 180cm and 240cm respectively. They are put into the small pieces which are of the same length. What is the greatest possible length for these pieces if no wood is left over?
b) By how much is the sum of ![]() and
and ![]() less than
less than ![]() ?
?
2. a) Mr.Kazidi walked a distance of 1 kilometre and 300 metres from his home to shop, he then walked further 0.85 kilometres to stadium to great his friends who was watching football. Calculate the total distance in metresKazidi travelled.
b) A rectangular tank has its internal measurements of 6.0m long, 3.5m wide and 4.9m high. Estimate the total litres that the tank can hold
3. a) If the degree of an interior angle of a regular polygon is twice the degree of exterior angle of it. Determine,
i) The size of an interior angle
ii) The number of sides of that polygon
iii) Sketch and name that polygon.
b) The area of Mr. Daslo trapezium plot is 143cm2. If the lengths of its parallel sides are 14cm and 8cm respectively. Find its height.
4. a) If 4 pens and 11 pencils costs 1240/- and 3 pens and 2 pencils costs 680/-. What are the cost of pen and pencils?
b) The product of two consecutive even numbers is 288. Work out for their sum.
5. a) Book seller bought 100 books for Tshs. 20,000/- . He sold 80% of them at a profit of 25% , 60% of the remaining at a loss of 5% , and the rest at the buying price. Find his overall profit.
b) Three people contributed Tshs. 45,000/- ,Tshs 30,000/- and Tshs. 25,000/- to start a business and they agreed also to share the profit obtained in the ratio of their investment. If the last one gets Tshs. 8000/-.
i) Find the total profit
ii) Find the shares obtained by the other two.
6. a) If the line whose equation is y = 3x – k passes through the points (6,10) and ( q, 22) . Find the value of k and q .
b) Point A ( 2, 1 ) is first reflected in the line x = -1 and then enlarged with a scale factor of 2 . Find the final image.
7. a) (i) Given the equation ![]() =
= ![]() , finding the values of a, b, c and d.
, finding the values of a, b, c and d.
b) Find the value of m in 3 – m log 2 = log 250 without using mathematical table.
8. a) PQR is an isosceles triangle, where by ![]() =
= ![]() , and
, and ![]() =
= ![]() . If S is a point between Q and R. Prove that
. If S is a point between Q and R. Prove that ![]() .
.
b) Triangles ABC and DEF are similar. Find the size of the angles labeled x, y, z and w.

9. a) The angle of elevation of the top of a vertical building from a point on the ground is 25![]() . The point on the ground is 80m away from the base of the building. By sketching a diagram representing this information. Calculate the height of the building ( write the answer correct to one decimal place.)
. The point on the ground is 80m away from the base of the building. By sketching a diagram representing this information. Calculate the height of the building ( write the answer correct to one decimal place.)
b) Without using mathematical tables, evaluate ![]()
10. a) A boy has 50 marbles , 35 marbles had some red mark and 20 marbles had some blue mark and 12 marbles had both red and blue mark.
i) Represent the information in the Venn diagram.
ii) How many marbles had neither red nor blue mark.
b) The following table shows distribution scores of 50 students in Geography examination.
| Class limit | 35 - 44 | 45 - 54 | 55 - 64 | 65 - 74 | 75 - 84 | 85 - 94 |
| Frequency | 4 | x | 10 | 12 | 6 | 8 |
i) Construct frequency distribution table.
ii) Draw a cumulative frequency curve
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iii) How many students failed if the pass mark was 65% ?
Page 1 of 11
FORM TWO MATHEMATICS EXAM SERIES 202
FORM TWO MATHEMATICS EXAM SERIES 202
THE OFFICE OF THE PRESIDENT, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT.
SECONDARY EXAMINATION SERIES
MARCH 2025
MATHEMATICS FORM TWO
TIME: 2:30HRS
INSTRUCTIONS
1. Answer all questions
2. All necessary working and answers for each question must be shown clearly.
3. NECTA Mathematical tables and non-programmable calculator may be used.
Answer all questions
1. A dog, a cat and a goat have masses of 30.75kg, 13.44kg and 48.26kg, respectively
- Calculate the total mass of all three animals
- Convert the answer obtained in (a) (i) into grams
(b) Round off
- 75000 correct to 2 significant figures
- 0.00015 to 4 decimal places
- 28.82 to tens
2. (a) (i) Add the first three multiples of 2, 3 and 5.
(ii) The numbers K, 2, 3 and 5 have an average of 5. What is the number represented by the letter K?
(b) Re-write the number ![]() as a mixed fraction.
as a mixed fraction.
3. (a) The number of pupils in three primary schools is as follows. Iganzo primary school is 1600 pupils, Ruanda primary school is 1500 pupils and Ilea primary school is 1800 pupils. Approximate the number of pupils of the three schools to the nearest thousands.
(b) Calculate ![]()
4. (a) A car was sold at a profit of 90000 shillings. If the rate of profit is ![]() % , find the purchasing price of the car and its selling price?
% , find the purchasing price of the car and its selling price?
(b) Mr. Juma deposited a certain amount of money in a bank for a period of 3 years at the rate of 3.5% which gives an interest of 8400 shillings. Determine the amount of money that Mr. Juma deposited initially.
5. (a) The weight of one female student at Maanga Primary School is 50kg and 750g. If there are 210 students of the same weight, find their total weight.
(b) Approximate 13.95 and 9.72 to the nearest tens, hence evaluate 13.95 x 9.72 by using the approximated number
6. (a) The interior angle of a regular polygon is four times as its exterior angle. Find
- The size of each exterior angle
- The number of sides
- State the name of a polygon
- The perimeter of a rectangle is 20cm and its area is 24cm2. Calculate the length and breadth of the rectangle.
7. (a) The line through the point A ![]() and B
and B ![]() has equal slope to that
has equal slope to that
![]() . Find the value of K.
. Find the value of K.
- The scale of the map is given by 1:50,000. Calculate the ground distance which is represented by 4.8cm on the map.
8. (a) Rectangular table top is 2m long. If the area of the rectangular table top is
3.96m2. find its width
(b) i. Solve the following simultaneous equations
2x+3y=5
4x+23=5y
ii. If Fatuma is 4 years less than Bakari and 3 times Fatuma's age is equal to 2 times Bakari's age. What are their ages ?
9. (a) (i) Find the equation of the straight line passing through (3,5) and (7,9).
(ii) Calculate the gradient and coordinates of the y-intercept of 2x+3y=12.
(b) Find the image of a point (-4, 3) after a reflection on y-axis followed by another reflection on y=0.
10. (a) One - third of the sum of ages of Ana and Asha is 50 years, and one - fifth of the difference of their ages is 2 years, find the age of Ana and Asha respectively.
(b) The width of the football ground is 40m. If the area of the same football ground is ![]() ;
;
(i) find the length of the football ground
(ii) if the person has to walk around the football ground, what length of the football ground is expected to be covered by the person?
FORM TWO MATHEMATICS EXAM SERIES 195
FORM TWO MATHEMATICS EXAM SERIES 195
PRESIDENT’S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES,
MID TERM ONE – MARCH-2024
MATHEMATICS FORM TWO
Time: ...........
Instructions
1. Answer all questions
2. All necessary working and answers for each question must be shown clearly.
3. NECTA Mathematical tables and non-programmable calculator may be used.
- (a) (i) Add the first three multiple of 2,3, and 5
(ii) The number K, 2, 3 and 5 Have an average of 5. What is the number represented by letter K?
(b) Re- writes the number 1.35 as mixed fraction
- The numbers of pupils in three Primary schools are as follows: Iganzo Primary Scchool 1600 pupils, Ruanda primary school 1500 pupils, Ilea Primary School 1800 pupils. Approximate the number of pupils of three schools to nearest thousands.
(b) Calculate (80kg 49g)-39kg 850 g
- (a) One – third of sum of ages of Anna and Asha is 50 yrs and one fith of difference of their ages is 2 yrs. Find the age of Anna and Asha respectively
(b) The width of a football pitch is 1700cm2. Find
- The length of football ground
- If a person walks around the pitch, what is the length of a football ground does the person cover?
- (a)Mr Amuti has three classes. Each class has 28, 42, and56 students respectively. Mr. Amuti wants to divide each class into groups so that every group and every class has the same number of students left over. What is the maximum number of students Mr Amuti can put into each group?
(b) A lorry carries 7.2 tonnes of sand from mining area to industrial site. On the way 230kgs of sand fall off. What is the remaining mass at the end of the journey?
- (a) Write 624.3278 to correct to
- Five significant figures
- Three decimal place
(b) A rope of 18m and 80cm is to be divided into four equal parts. How long will each part br. (give your answer in meter and centimeter
- (a)Solve 3 -
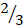 of (6x+9)=5-2x
of (6x+9)=5-2x
(b) If Fatuma is 4 years less than Bakari and 3 times Fatima’s age is equal to 2 times Bakari’s age. What are their ages?
- (a) John, Ramadhani, Marry and Sam have 600, 100, and 300 shares in a cooperative shop respectively. Divide 150,000 sh among them in a ration of their shares
(b) A real estate agent received a 6% discount on selling price of a house. If the discount was Tsh 888,000. Find the selling price of the house.
- (a) Equal squares are large as possible are drawn on a rectangular board measuring 54 cm by 78 cm. Find the largest size of the squares
(b) Express 2.79 as a fraction in form a/b where a and b are integers and b#0
(ii) Arrange 2/5, 5/7, 48% and 0.6 in ascending order.
- (a) Solve for x if
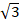 x+2+17=8
x+2+17=8
(b) If log 2= 0.30103, and lob 3 = 0.47712, evaluate log 48
- (a) The line through the point A (k,4) and B (3,2k) has a slope to that y+3x-4=0. Find value of k
(b) The scale of a map is given by 1:50,000. Calculate the ground distance which is represented by 408cm on the map
FORM TWO MATHEMATICS EXAM SERIES 171
FORM TWO MATHEMATICS EXAM SERIES 171
PRESIDENT’S OFFICE REGIONAL ADMINISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSESSMENT
MATHEMATICS FORM TWO
MID TERM EXAMS-AUG – 2023
041
Time: 2:30 Hours AUG, 2023
INSTRUCTIONS
1. This paper consists of a total ten (10) compulsory questions
2. Show your work clearly
3. All writing must be in blue or black ink, except drawings which should be in pencil
4. All communication devices, programmable calculators and any unauthorized materials are not allowed in the examination room
1 a) The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 10 seconds respectively. If they change simultaneously at 7a.m at what will they change simultaneously again?
b) If x = 0.567567567... and y – 0.83 by converting these decimals to
fractions, find the exact value of ![]() in simplest form
in simplest form
2 a) If T= 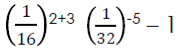
Find the value of t
b) Write ‘’L’’ in terms of M, N and T from the formula =
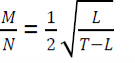
c) Determine the value of x if log5(x+1)-1=log5(x-3)
3. a) A lorry carries 7.2 tonnes of sand from the mining area to the industrial site. One the way 230kg of sand either fall off or blow away. What mass of sand will remain by the end of the journey? Give the answer in tonnes b) An article was sold for sh 160,000 at a profit of 25% find the buying price
of the article
4. a) Solve for the quadratic X2 – 8x +7 = 0
b) Solve for x and y if;
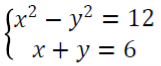
5. a) The sum of two numbers is 127. If the difference/ between numbers is 7, find the numbers.
b) If : = 2:3
FORM TWO MATHEMATICS EXAM SERIES 161
FORM TWO MATHEMATICS EXAM SERIES 161
PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM TWO
MID-TERM EXAMS-MARCH – 2023
- (a)Solve
By elimination method
(b)The length of a book exceeds its width by 5cm. Calculate the dimensions of the book given that its area is 50cm2
- (a) A rectangular table top is 2m long. If the area of the rectangular table top is 3.96m2 find its width
(b)(i)Solve the following simultaneous equation
2x + 3y=5
4x + 23 = 5y
(ii) If Fatuma is 4years less than Bakari and 3 times Fatuma’s age equal to 2 times Bakari age. What are their ages?
- (a)(i)x2 + bx + c= (x – 3) + 2) determine the value of b and c
(i) If x2 + ax + 4 = 0 is a perfect square. Find value of a
(iii)Solve the following quadratic equation by completing the square method x2+6x+7 = 0
(b)Solve
- (a)Asha and Juma received 630,000 shilling from their father. The father wanted to give Asha twice an much money as the amount that could be given to Juma. How much did Asha receive
(b)Mr and Mrs. Juma deposited some money in a bank that pays a simple interest of 3% per annum. After 4 years they eamed an interest of 900,000 shillings Determine the amount of money
Determine the amount of money
- Deposited initially
- Accumulated after a period of four years
- (a)if the line equation is y=3x – p passes through points (6, 10) and (9, 22) find the value of P and Q
(b)A mason wants design a small room 500cm. by 200cm.
(i)Draw a diagram of a room at a scale of 1.100
(ii)Calculate the area of the room using the result of 6 (b)(i)
- (a)(i)Write 498,030 in words
(ii)Express the number given in part (a)(i) in standard rotation
(iii)By using listing method, write down lowest common multiple of 3, 10, and 15
(b)(i)Write in numeral; Nine hundred ninety million nine hundred ninety nine thousand, nine hundred and one.
(ii)Determine the number of significant figures in each of numbers, 400, 780 and 0.00606, then approximate each number into one significant figure.
- (a)Find the value of x in the equation
(b) If , Find the value of x
- (a)If
Find value of x and Y
(b)(i) Find value of 0.0000234 x 120 in standard rotation correct is 3 significant figures
(ii)Rationalize the denominator of the expression
- (a) A machine that costs shs 180,000 was sold at a profit of 40%. Find the selling price
(b)A father divided shs 150,000 among Rose and Japheth in the ratio of 2:3 respectively. How much money did each get?
- (a)Find the value of x equation 9 x 34x+ = 27(x – 1)
(b)Factorize the expression 6x4x – 11x + 4 by splitting the middle term.
FORM TWO MATHEMATICS EXAM SERIES 140
FORM TWO MATHEMATICS EXAM SERIES 140
THE UNITED REPUBLIC OF TANZANIA
PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCY BASED EXAMS
FORM TWO PRE-FTNA ASSESSMENT
041 BASIC MATHEMATICS
TIME: 2:30 hours October, 2022
Instructions
- This paper consists of 10 questions.
- Answer all questions.
- Cellular phones are not allowed in the Examination rooms.
- Write you examination number on every page of your answer sheet(s)
| FOR EXAMINER’S USE ONLY | ||
| QUESTION NUMBER | SCORE | EXAMINER’S INITIAL |
| 01 |
|
|
| 02 |
|
|
| 03 |
|
|
| 04 |
|
|
| 05 |
|
|
| 06 |
|
|
| 07 |
|
|
| 08 |
|
|
| 09 |
|
|
| 10 |
|
|
| TOTAL |
|
|
| CHECKER’S INITIAL |
|
|
- (a)( i) Find the sum of all prime numbers between 3 and 23 inclusively.
(ii) When two different signs are multiplied, a product is obtained. Multiply the product obtain with a negative sign. Give the last sign you Will obtain.
- Change 0.
 into a simplest fraction then express your answer into percentage
into a simplest fraction then express your answer into percentage
- (a) Write 0.07
 correct to
correct to
(i) Four significant figures
(ii) Four decimal places
(b) write 20.025 into hundredth.
(c) Aisha’s mom took 30 minutes to cut the vegetables, and she took 1 hour in cooking. Find how many Seconds she took to complete the whole cooking?
3. (a) In the figure below M<RTS = 80
FORM TWO MATHEMATICS EXAM SERIES 131
FORM TWO MATHEMATICS EXAM SERIES 131
THE UNITED REPUBLIC OF TANZANIA
PRESIDENT’SOFFICEREGIONALADMINISTRATIONANDLOCALGOVERNMENT
COMPETENCY BASED EXAMS
FORM TWO PRE-FTNA ASSESSMENT
041 BASIC MATHEMATICS
TIME:2:30hours October,2022
Instructions
- This paper consists of 10 questions.
- Answer all questions.
- Cellular phones are not allowed in the Examination rooms.
- Write you examination number on every page of your answer sheet(s)
| FOR EXAMINER’S USE ONLY | ||
| QUESTIONNUMBER | SCORE | EXAMINER’S INITIAL |
| 01 | ||
| 02 | ||
| 03 | ||
| 04 | ||
| 05 | ||
| 06 | ||
| 07 | ||
| 08 | ||
| 09 | ||
| 10 | ||
| TOTAL | ||
| CHECKER’S INITIAL | ||
- (a)( i) Find the sum of all prime numbers between 3 and 23 inclusively.
(ii) When two different signs are multiplied, a product is obtained. Multiply the product obtain with a negative sign. Give the last sign you Will obtain.
- Change 0.
 into a simplest fraction then express your answer into percentage
into a simplest fraction then express your answer into percentage
- (a) Write 0.07
 correct to
correct to
(i) Four significant figures
(ii) Four decimal places
(b) write 20.025 into hundredth.
(c) Aisha’s mom took 30 minutes to cut the vegetables, and she took 1hour in cooking. Find how many Seconds she took to complete the whole cooking?
3. (a) In the figure below M<RTS = 80
FORM TWO MATHEMATICS EXAM SERIES 129
FORM TWO MATHEMATICS EXAM SERIES 129
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCY BASED SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS FORM TWO
INSTRUCTIONS
- This paper consist of ten (10 questions
- Answer all questions in the spaces provided
- Show clearly all necessary working
- Where necessary mathematical table may be used
- Cellular phones, calculators and any unauthorized materials are not all allowed in examination room
- Write your index number at the top right corner of every page.
- Re-arrange the digits in the number 391587 to form the largest and smallest possible numbers.
- (a)Given that
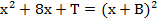 Find the value of T and B
Find the value of T and B
(b) Find the value of n if ![]()
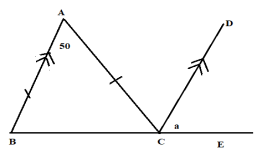
- Find the size of the angle marked “a” in the figure below
- (a) Find the time in which Tsh 400,000 will earn Tsh 96,000 at the rate of 12%
(b)What is the product of LCM and GCF of 16,24 and 36
- (a)Given (x + 40°) and (2x + 5°) are complementary angles, find the value of x
(b)Rationalize the denominator to the simplest form
![]()
- (a)Factorize the expression 6x2 – 11x + 4 by splitting the middle term
(b)By using elimination method solve for x and y in
4y – 41=-14x
6x – 30 – 10y
- (a)If
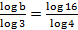 Find the value of b
Find the value of b
(b)By using mathematical table evaluate
![]()
- (a)The line
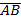 passed through the point A(2,y) and (5,7) have the slope of
passed through the point A(2,y) and (5,7) have the slope of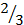 . What is the value of y?
. What is the value of y?
(b)What is the centre of an enlargement, given that the image of A(3,2) under the enlargement scale factor 2 is A(6,4)?
- In a class of 60 students 47 are taking physics while 33 are taking mathematics. If there are 2 students who are taking neither Physics nor Mathematics and 22 are taking both Physics and mathematics
- Represent this information by Venn diagram.
- How many students are taking mathematics only?
- The following are the Mid-term test marks of 80 form two Mathematics students from Mtoni Secondary School
| Marks in % | 25 | 35 | 45 | 50 | 65 | 75 | 80 | 85 |
| Numbers of students | 14 | 18 | 11 | 10 | 5 | 14 | 2 | 6 |
- Which mark was scored by largest number of students?
- Which mark was scored by small number of students?
- What is the difference between the number of students passed the test and those who failed if the pass mark was 50%
FORM TWO MATHEMATICS EXAM SERIES 119
FORM TWO MATHEMATICS EXAM SERIES 119
FORM TWO TERMINAL EXAMINATION
BASIC MATHEMATICS
Time: 2:30 Hours Year : 2022
Instructions
1. This paper consists of ten (10) compulsory questions.
2. Show clearly all the working and answers in the space provided.
3. All writing must be in blue or black ink except drawings which must be in pencil.
4. NECTA mathematical tables, geometric instruments and graph papers may be used where necessary.
5. All communication devices, calculators and any unauthorized materials are not allowed in the assessment room.
6. Write your Assessment Number at the top right corner of every page.
1. (a) Calculate the sum of the GCF and LCM of 42, 45, 50.
(b)![]()
2.(a) Convert (i)256800cm into km
(ii)0.125 into percentage
(b) Round off (i) 260743 to the nearest thousand
(ii) 0.04261 to three decimal places
3.(a) Factorize the expression ![]()
(b)![]()
4. (a) Make A the subject of the formula ![]()
(b) If 4tanB=3 and B is an acute angle, find the value of;
- Cos B
- 4 tan B + sin B
(c) A straight line passes through two points A(-3, 6) and B (-6, 3). Find the gradient of the line AB
5. (a) Find (i) the largest possible number; and
(ii) The smallest possible number by changing order of the digits in 47986.
(b).Write 0.0.346 in standard form.
6. (a) In a certain office, every man owns either a car or a lorry or both 23 own lorries, 14 own cars and 5 own both lorries and cars. How many men are there in that office?
(b) .Joyce used 1/3 of her money to buy sugar, 1/4 of it to buy soap and she remained with Shs 35/=
- How much money did she have at the beginning?
- How much money did she use to buy sugar?
7. (a) Simplify ![]()
(b)Use a number line to find the sum of ![]()
(c)Arrange 2/5, 5/8, 48% and 0.6 in ascending order of magnitude.
(d)Decrease 160,000 by 16%
8. (a) Rationalize the denominator of ![]()
(b) Show on the number line the solution set of the inequality ![]()
9. (a)Without using Tables evaluate ![]()
(b)Given A=1/2 where A is an acute angle, find the value of 1 – cos2 A.
10. (a) Simplify ![]()
(b)If N=2x10-8 find the value of 1/N in scientific form
(c) Find the equation of a line through the point (2, -2) crossing the y-axis at the same point as the whose equation is ![]()
FORM TWO MATHEMATICS EXAM SERIES 106
FORM TWO MATHEMATICS EXAM SERIES 106
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM TWO BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 2:30 Hours Year: 2022
Instructions
1.This paper consists of ten (10) compulsory questions.
2.Show clearly all the working and answers in the space provided.
3.All writing must be in blue or black ink except drawings which must be in pencil.
4.NECTA mathematical tables, geometric instruments and graph papers may be used where necessary.
5.All communication devices, calculators and any unauthorised materials are not allowed in the assessment room.
ATTEMPT ALL QUESTIONS
1. (a)(i)List down all the prime numbers between 1 and 12 and represent the numbers on the number line
(ii) Find the H.C.F and L.C.M of the numbers 8, 12 and 20 by prime factorization
(b)(i) Evaluate
![]()
(ii) Evaluate ![]()
(iii)Evaluate
![]()
(c)Evaluate
![]() .
.
Write your answer in repeating decimal notation
2. (a) The distance between two points is 30.567km. Write the distance in metres in one significant figure
(b) The velocity of a car between two stations AB and BC is 40m/sec and 60km/hr. respectively. Find the average velocity in m/minute assuming that AB and BC are straight roads
(c)If 6,000/= amount to 9,600/= in five years simple interact what is the percentage rate?
3. (a) Given that the rectangle ABCD is similar to rectangle MBCN below
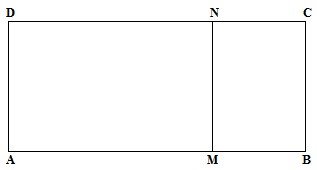 |
AB=10 BC=6 and
NC=x
(i )Find the value of x
(ii) Verify that the ratio of the areas = k2 where k is the ratio of the sides
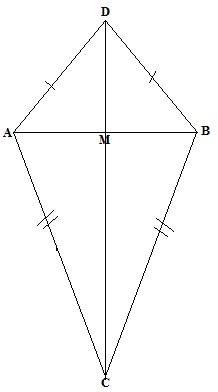
(b)If ![]() is isosceles where AD=BD and E and C are the mid-points of AD and BD
is isosceles where AD=BD and E and C are the mid-points of AD and BD
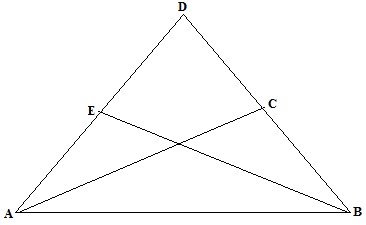
Prove that ![]() (congruent)
(congruent)
4. (a)Evaluate
i. ![]()
ii. ![]()
(b)Solve for x and y
i. ![]()
ii. If x=5 and y=3, Find the value of ![]() ,
,
(c) If ![]() , make p the subject
, make p the subject
5. (a)Find the value of
i. ![]()
ii. ![]()
(b)Find x
i. ![]()
ii. ![]()
(c)With the use of common logarithm find x
i. ![]()
ii. ![]()
6. (a) A and B are two intersecting circles of radius 4cm and 6cm respectively. Find the area enclosed by A![]() B, is 10cm2, find the area enclosed by the circles (shaded)
B, is 10cm2, find the area enclosed by the circles (shaded)
(b) In figure below, Triangles ABD and ABC are two isoscetes triangles CD=36cm, AB=12cm and ![]() Find the area of the figure ACBD
Find the area of the figure ACBD
(c)Find the area of squire whose length of the diagonal = 6cm
7. (a)Find the equation of the line perpendicular to the 2y – x – 6=0 and passing through the point (4,6)
(b) Represent the equation in (a) in forms
i. y=mx+c
ii. ![]() (A and B are x-intercept and y-intercept)
(A and B are x-intercept and y-intercept)
(c) The point A (4, 3) is reflected in the line y=x. What are the coordinates of the image?
8. (a)(i)Express; ![]() as a perfect squire
as a perfect squire
(ii) If (6+x)(8+x) = ![]() find the value of a and b
find the value of a and b
(b) Factorize.
i. ![]()
ii. ![]()
iii. ![]()
(c) Evaluate ![]()
9. (a) An item is sold at 480,000/= with profit of 20%
i. Find the ratio of the buying price to the selling price
ii. If the same item would be sold at 360,000/= what would be the percentage lose ?
(b)Find the interest for a principal of 100,000/= at 4% compound interest after 10years
(c)Tarimo wants to borrow 10 million Tanzania shillings from a Bank to promote his business. The Bank agree to charge his compound interact at 10% per year. How much interest Mr. Tarimo will owe the bank at the end of 5 years?
10. (a)Solve the equation: ![]() by
by
i. Factorization
ii. Completing the square (using the formula)
(b) Solve the following simultaneous equation
i. ![]()
ii. ![]()
(c)Solve the following inequalities
i. 3x + 6 < 10 – 5x
ii. ![]()
FORM TWO MATHEMATICS EXAM SERIES 105
FORM TWO MATHEMATICS EXAM SERIES 105
PRESIDENTS OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM 2 BASIC MATHEMATICS
SECTION A (60 MARKS)
1. Rearrange the digits 39175 to form
- The greatest possible number
- The smallest possible number
2. Mary used tiles to build the floor of her sitting room measuring 15m by 20m. If she used only whole ones and they were alike, what was the greatest size of each tile?
3. The operation on the integers P and Q is defined as P*Q=PQ + 2P-3Q, find the value of
- 2*3
- Q if 2*Q=20
4. Find![]()
5. Factorize the expression 15x2 + xy 6y2
6. In 2011 the population of a village was 800. It increased by 20% the following year. What was the population in the year 2012?
7. In triangle ABC below x° is 18° less than y°. Find the values of x° and y°.
8. If![]() find the value of
find the value of ![]()
9. Find the length of time between 0425 hours and 1812 hours
10. If the product of 5 integers is negative, What is the maximum number of integers in that product which are positive?
11. Make L the subject of the formula. ![]()
12. Simplify the expression ![]()
13. Find the rational number in the form ![]() where a and b are integers and
where a and b are integers and ![]() from the Number
from the Number ![]()
14. Given that ![]() Find the value of x +y.
Find the value of x +y.
15. Factorize the expression ![]() hence use the result to evaluate:
hence use the result to evaluate: ![]()
16. Find the equation of a line which passes through the points A(4,2) and B(5,3) giving your answer in the form y=mx + c
17. Express the following numbers in scientific notation (A)72500 (B)0.001325
18. Solve for x in the equation ![]()
19. If![]() =1. Find the value of x
=1. Find the value of x
20. If shs.600/= amounts to 960=for 5years, what is the percentage rate of simple interest per annum?
SECTION B (40 MARKS)
21. (a)Given that ![]()
(b)Use Mathematical tables to find the value of ![]()
22(a) Let A and B be two sets such that n(A)=52, n(B)=60 and (AUB)=96. Find tn(A-B)
(b)In a certain area 50 householders were asked if they had a radio set, a T.V. set or both 40 householders said they had a T.V. set, 30 had both a radio set and a T.V. set and 2 householders had neither. With the help of a Venn diagram, how many householders had a radio set but no T.V set?
23. The upper part of a tree broken by the wind falls to the ground without being detached. The top of the broken part touches the ground at an angle of 36°30 at a point 5 metres from the foot of the tree. Calculate.
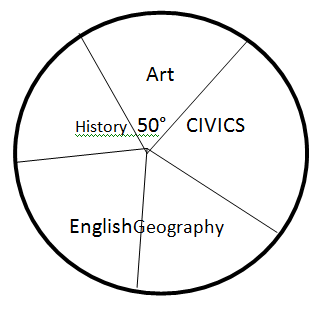
24. (a)The pie chart below shows the number of students in one examination Centre in Different subjects sat for the national examination.
1
FORM TWO MATHEMATICS EXAM SERIES 95
FORM TWO MATHEMATICS EXAM SERIES 95
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
ANNUAL EXAMINATION
FORM TWO
BASIC MATHEMATICS
041
TIME: 2:30 HOURS November, 2021
![]()
Instructions
1. This paper consists of ten (10) compulsory questions.
2. Answer ALL questions
3. Each question carries ten (10) marks.
4. Show clearly all the workings and answers in the spaces provided.
5. All writings must be in blue or black ink except for drawings which must be in pencil.
6. Four figures/mathematical tables, geometric instruments and graph papers may be used where necessary.
7. Calculators, cellular phones and any unauthorized materials are not allowed in the examination room.
8. Write Your Examination Number at the top right corner of every page.
| FOR EXAMINER’S USE ONLY | ||
| QUESTION NUMBER | SCORE | EXAMINER’S INITIALS |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| TOTAL |
|
|
| CHECKER’S INITIALS |
| |
1. (a) Three bells ring at intervals of 20 minutes, 30 minutes and 40 minutes. If they start ringing together at 7.30 am
(i) After how long will they ring together again?
(ii) At what time will this be?
(b) Round off 349.678 to the nearest.
(i) Tens
(ii) Hundredth
(iii) One significant figure
2. (a) Write ![]() in form of
in form of ![]() , where b ? 0.
, where b ? 0.
(b) In a class of 40 students ![]() are boys. Two fifth of the girls wear spectacles.
are boys. Two fifth of the girls wear spectacles.
How many girls do not wear spectacles?
3. 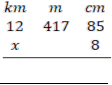 (a) Perform:
(a) Perform:
(b) Find the time in which sh 200,000/= will earn sh 48,000/= at the rate of 4% interest per annum.
4. (a) Calculate the angles marked with letters X, Y and Z.

(b) Find the area of rectangle whose perimeter is 30cm and its length and width are (3W-7) cm and (W+2) cm respectively.
5. (a) Factorize the expression
6x2 – 11x + 4 by splitting the middle term.
(b) The sum and difference of the two numbers are 9 and 3 respectively. Find the possible numbers.
6. (a) (i) Find the equation of the straight line passing through (3,5) and (7,9).
(ii) Calculate the gradient and coordinates of the y-intercept of 2x+3y=12.
(b) Find the image of a point (-4, 3) after a reflection on y-axis followed by another reflection on y=0.
7. (a) If ![]() -4x+2 =
-4x+2 = ![]() 9. Find the value of X.
9. Find the value of X.
(b) Rationalize ![]() writing the answer in the form a
writing the answer in the form a![]() where a, b, c and d are real.
where a, b, c and d are real.
(c) Given log2 = 0.3010, log3 = 0.4770 and log7 = 0.8451. Find the value of log294.
8. (a) Calculate the length of EC and CD in figure below:
B D
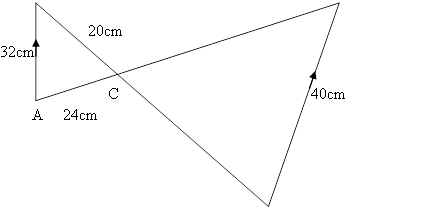
E
8. (b) Use the figure below to prove that triangle ADB? Triangle ADC
A
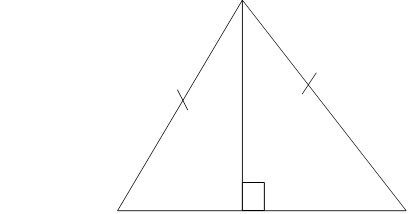
C D B
9. (a) A rectangle has sides of 12mm and 16mm. Calculate the length of one of its diagonals.
(b) Calculate the exact value of ![]() .
.
10. (a) In the Venn diagram below:
U = { Boys in form II at a certain secondary school}
F = { Members in the football team}
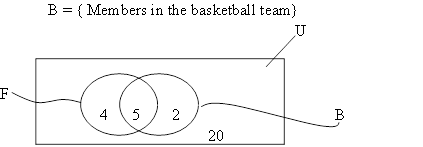
(i) How many boys are in the football team?
(ii) How many boys are in both teams?
(iii) How many are in the football team but not in the basketball team?
(iv) How many are neither basketball nor football team?
(v) How many boys in form II at the school?
10. (b) The table below shows the distribution of the score of 60 students in Mathematics table at MJI MWEMA secondary school.
| Marks % | 45 – 55 | 56 – 66 | 67 – 77 | 78 – 88 | 89 - 99 |
| No. of students | 11 | 15 | X | 17 | 10 |
(i) Find the value of X.
(ii) Find the percentages of the student score ate most 77 marks.
FORM TWO MATHEMATICS EXAM SERIES 73
FORM TWO MATHEMATICS EXAM SERIES 73
Student’s Assessment Number……………..……
MINISTRY OF EDUCATION AND VOCATION TRAINING
MID TERM EXAMINATIONS
041 BASIC MATHEMATICS
TIME 2:30 HOURS AUG: 2021
Instructions
- This paper consists of ten (10) compulsory questions.
- Show clearly all the working and answers in a space provided.
- All writing must be in blue or black ink except drawing must be in pencil.
- Mathematical tables, geometric instruments and graph papers may be used where necessary
- All communication devices and calculators are not allowed in assessment room.
- Write your assessment Number in top write corner of every page.
| FOR ASSESSOR’S USE ONLY | |||||||||||||||||||||||||||||||||||||||
|
- (a) Find the sum of all prime numbers between 80 and 100
(b) Round off:
(i) 9.67 to ones,
(ii) 0.205 to one decimal place,
(iii) 0.197 to two decimal places,
Hence, estimate the value of ![]()
2. (a) Evaluate 0.4 + 25% ![]() (0.22
(0.22![]() 0.2) +
0.2) + ![]() 0.45)
0.45)
(b) If the new price of selling shoe is 40000Tsh. Findthe percentage increase of price if the old price was 30000Tsh.
3. (a) If the bus starts the journey from Babati at 0600 and takes eight hours and a half to reach at Chemba bus terminal. Write the time taken to reach in 24 hours clock.
(b) If 50000Tsh of money was invested at a bank which provide the rate of 5%. Find the amount at a bank after 4 years.
4 (a) Find the value of an angle marked in letter f,g and k in the figure below.
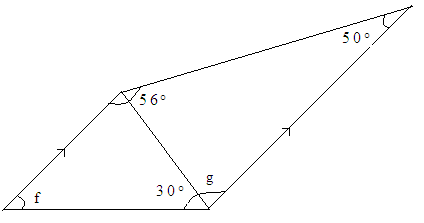
b) Find the perimeter of square ,if its area is 36cm2
5 (a) The sum of two numbers is 127. If thedifference between the number is 7, Find the numbers
(b) Solve the equation ![]() by using quadratic formula.
by using quadratic formula.
6 a) If the line passes through the point (3,4) and (2,6). Find
- The slope of the line.
- The equation of line in form of Y = MX+C
b) The vertices of the triangle are A(2,2) , B (3,4) and C (4,3). If the triangle is reflected under x-axis ,Write down the coordinate of the image of points A, B and C
- (a)Find the value of p given that (
 )2p +1 = (
)2p +1 = ( )3p.
)3p.
(b) (i) Find the value of 0.0000125 ![]() in standard notation.
in standard notation.
(ii) Simplify the expression (3 + ![]() ) (4
) (4 ![]() )
)
8 (a) solve for the x in the inequality
3X – 4>, X+16
(b) Factorize the expression a2-b2
Hence find the exact valueof 6722-3282
9 the right angled triangle in the figure below has sides of length 7![]() , 24
, 24![]() cm and 150cm
cm and 150cm
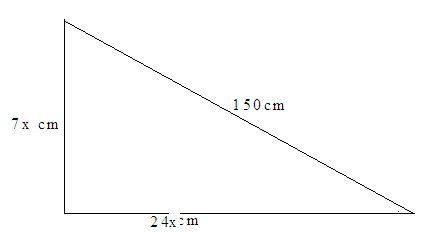 S
S
(a)Calculate the value of![]() .
.
(b)Calculate the area of the triangle
10 (a) There are 48 men at the meeting of whom 24 are teachers, 36 are parents and 16 are both teachers and parents . By using venndiagram , find the number of men who are neither teacher nor parents.
b) The marks of 100 student were recorded as follow,
| Marks | 41 - 50 | 51 -60 | 61 - 70 | 71 - 80 | 81 -90 | 91 - 100 |
| Number of students | 10 | 22 | 34 | 25 | 7 | 2 |
- Which mark were scored by many student ………………………………….
- Which marks was the lowest mark ………………………………………………….
- If 50% was the pass mark of the test if above 50%, How many student passed examination
FORM TWO MATHEMATICS EXAM SERIES 70
FORM TWO MATHEMATICS EXAM SERIES 70
Candidate’s Examination Number………………………………
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS MID TERM EXAMINATION
FORM TWO-2021
Time: ![]() Hours 20th March 2021
Hours 20th March 2021
Instructions
- This paper consists of ten (10) compulsory questions.
- Answer all questions showing clearly all the working and answers in the spaces provided.
- All writing must be in blue or black ink except drawing which must be in pencil.
- All communication devices and calculators are not allowed in the examination room.
- Write your Examination Number at the top right corner of every page.
---------------------------------------------------------------------------------
- (a) Find the sum of the LCM and GCF of 13, 52 and 104.
(b) Juhudi village received 586 389 bags of fertilizers for distribution to farmers. Round off this number to the nearest thousands and ten thousands
- (a) Find the unknown numbers in the following equivalent fractions.
![]()
(b) Change ![]() into a recurring decimal
into a recurring decimal
- (a) Change 15 km into centimeters
(b) Find the time in which sh.200 000 will earn sh.48 000 at the rate of 4% simple interest per annum.
- (a) In the following figure, find the size of the angles labeled
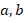 and
and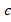 . (give reasons for your answers)
. (give reasons for your answers)
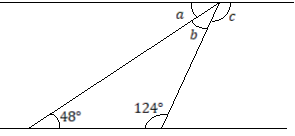
(b) A square has an area of![]() , find its perimeter.
, find its perimeter.
- (a) Find the equation of the straight line passing through the points
 . (Express your answer in the form
. (Express your answer in the form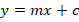 ).
).
(b) Solve the absolute valued equation: ![]()
- The sum of interior angles of a regular polygon is
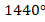 .
.
- Find the number of sides of the polygon
- Find the size of each exterior angle
- What is the name of the polygon? ____________________________
- (a) Find the value of
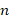 in the equation:
in the equation: 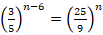
(b) Factorize the expression ![]() by splitting the middle term.
by splitting the middle term.
- (a) Rationalize the denominator and simplify
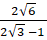
(b) Given the formula: ![]() make
make ![]() the subject of the formula.
the subject of the formula.
- (a) What number must be added to the expression
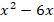 to make it a perfect square?
to make it a perfect square?
(b) Given that ![]() find the value of
find the value of ![]()
- (a) Use the factors of the difference of two squares to find the value of
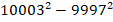
(b) Solve the following pair of simultaneous equations by elimination method ![]()
Page 1 of 8
FORM TWO MATHEMATICS EXAM SERIES 54
FORM TWO MATHEMATICS EXAM SERIES 54
Candidate’s Examination Number………………………………
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS MID TERM EXAMINATION
FORM TWO-2021
Time: ![]() Hours 20th March 2021
Hours 20th March 2021
Instructions
- This paper consists of ten (10) compulsory questions.
- Answer all questions showing clearly all the working and answers in the spaces provided.
- All writing must be in blue or black ink except drawing which must be in pencil.
- All communication devices and calculators are not allowed in the examination room.
- Write your Examination Number at the top right corner of every page.
---------------------------------------------------------------------------------
- (a) Find the sum of the LCM and GCF of 13, 52 and 104.
(b) Juhudi village received 586 389 bags of fertilizers for distribution to farmers. Round off this number to the nearest thousands and ten thousands
- (a) Find the unknown numbers in the following equivalent fractions.
![]()
(b) Change ![]() into a recurring decimal
into a recurring decimal
- (a) Change 15 km into centimeters
(b) Find the time in which sh.200 000 will earn sh.48 000 at the rate of 4% simple interest per annum.
- (a) In the following figure, find the size of the angles labeled
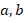 and
and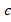 . (give reasons for your answers)
. (give reasons for your answers)

(b) A square has an area of![]() , find its perimeter.
, find its perimeter.
- (a) Find the equation of the straight line passing through the points
 . (Express your answer in the form
. (Express your answer in the form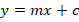 ).
).
(b) Solve the absolute valued equation: ![]()
- The sum of interior angles of a regular polygon is
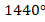 .
.
- Find the number of sides of the polygon
- Find the size of each exterior angle
- What is the name of the polygon? ____________________________
- (a) Find the value of
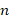 in the equation:
in the equation: 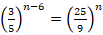
(b) Factorize the expression ![]() by splitting the middle term.
by splitting the middle term.
- (a) Rationalize the denominator and simplify
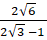
(b) Given the formula: ![]() make
make ![]() the subject of the formula.
the subject of the formula.
- (a) What number must be added to the expression
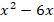 to make it a perfect square?
to make it a perfect square?
(b) Given that ![]() find the value of
find the value of ![]()
- (a) Use the factors of the difference of two squares to find the value of
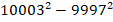
(b) Solve the following pair of simultaneous equations by elimination method ![]()
Page 1 of 8
FORM TWO MATHEMATICS EXAM SERIES 53
FORM TWO MATHEMATICS EXAM SERIES 53
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
MATHS- TERMINAL EXAMINATION-MAY
FORM TWO
Time 2:30 Hours MAY 2020
Instructions
- This paper consists of two sections A and B.
- Answer all questions in both sections
- Show clearly all working for each question
- Geometrical instruments and graph paper may be used where necessary
- Use
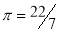
SECTION A (60 MARKS)
1. a) Rearrange the following in ascending order ![]()
b) Write 56 as the product of prime factors
2. Express ![]() in form of
in form of ![]() where p and q are both integers and
where p and q are both integers and ![]()
3. A room of length 270cm and 150cm is to be covered with square tiles. What is the largest size of the tiles to be used if no space of the room is left to be uncovered and how many tiles will be used?
4. Round off 34.9545 correct to i) Two significant figure ii) One decimal places
5. Write the following into 24-hours system i) 03: 15 Pm ii) 01: 01Pm
6. Given 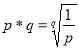 , find i) 64*3 ii) a if
, find i) 64*3 ii) a if ![]()
7. Two angles of pentagon are 580 and 380 and the other remaining three are in the ratio of 5:6:7. Find the largest angle.
8. Given a straight line 2y+5x+1=0, f
Fnd a) Slope b) y-intercept c) x-intercept
9. Two supplementary angles differ by 120. Find the angles.
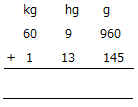
10. Add the following
11. Anna is two years older than betty. Last year, Anna was two times as old as Betty. What is their age?
12. Make r-subject of formula in the following ![]()
13. Express ![]() in the form of
in the form of ![]()
14. Use method of difference of two squares to evaluate the following
i) ![]() ii) 0.9852 – 0.0152
ii) 0.9852 – 0.0152
15. Given log2=0.3010 and log7=0.8451, without using logarithm table evaluate:
a) log1.25 b) log 3.5
16. Factorize the following expression
a)15t2-14t-8=0 b) (2c+3)2 – c2
18.Simplifythe following
a)![]()
b) 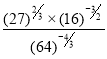
19. Expand the following
a) [y- 3] [ ![]() + y ] b) (6n -
+ y ] b) (6n - ![]() )2
)2
20. For value of P which makes the following equations perfect square
(i) x2 – Px +16=0
(ii) x2 - ![]() x + P=0
x + P=0
SECTION B (40 MARKS)
21. a) From the quadratic equation ![]() show that
show that 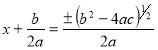
b) By using general formula of quadratic equation solve the following equation ![]()
22. The figure ABCD below is rectangle with sides as shown where C1 and C2 are two quarter circles inside it.
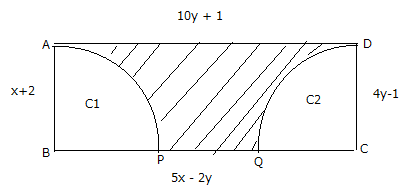
Find:
a) Value x and y shown in the figure
b) Perimeter of the rectangle
c)Area of the rectangle ABCD
d) Area of the shaded region
23.a) A rope is tired at the top of the flagpole and the other end of the rope is fixed on a point 36m from the base of the flagpole. If the flag pole is 15m high, what is the length of the rope?
b) In the figure below find the length of PQ and PS if QR=8cm, RQ=12cm and PR=17cm.
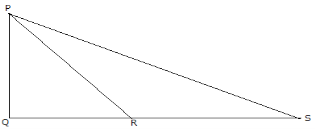
24. A farmer sold a quarter of his maize harvest and give one third of the remaining to his relatives. If the farmer remained with 36 bags of maize, find:-
a) How many bags of maize did the farmer harvest.
b) How many bags of maize did the farmer sold.
25. a) By using logarithm tables, evaluate 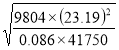
b) Evaluate the following without using logarithm tables:
(i) ![]()
(ii) 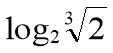
(iii) 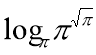
FORM TWO MATHEMATICS EXAM SERIES 14
FORM TWO MATHEMATICS EXAM SERIES 14
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
MID TERM EXAMIATIONS
024 MATHS- TWO
Duration: 2:30 Hours
INSTRUCTIONS.
- This paper consists of two sections A and B.
- Answer all questions in both sections
- Show clearly all working for each question
- Geometrical instruments and graph paper may be used where necessary
SECTION A (60 MARKS)
1. Write the place value of digits in the brackets
a) 1485361 (8)
b) 7524693 (2)
2. Write the following into expanded form
a) 470059 b) 1290400
3. Round off 309.437 correct to
i) 2-significant figure ii) 2-decimal places
4. Change the following into 12-hours system
i) 0404 hours ii) 0028 hours
5. Convert the following into fraction
i) 0.34 ii) 2.13
6. Find the greatest number that is exactly divides 360 and 456
7. Find solution of ![]() and show it no the number line.
and show it no the number line.
8. Divide Sh. 1690 among Peter, Juma and Ali in the ratio of ![]()
9. There are 180 members of a committee. In a meeting, ![]() were present. How many members were absent?
were present. How many members were absent?
10. Find 
11. Simplify the following
a) ![]()
b) ![]()
12. Solve the following equation
![]()
13. Find slope, x-intercept and y-intercept of line 5x-2y-7=0
14. The ratio of exterior to interior angle of regular polygon is 5:7.
Find number of sides of the polygon and total degree measure of the polygon.
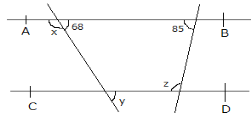
15. In a figure beside, AB//CD and line PQ and RS are transversal line. Find values of the angles marked x, y and z
16. In how many years would sum of the money double itself at 8% rate per annum?
17. Factorize the following expression a) 8x2 + 2x -3 b) x2-15x +58
18. By selling a computer for Sh. 800,000/=, a profit of Sh. 200,000/= is earned. Find the percentage profit.
19. Simplify the following
i) ![]()
ii)![]()
20. Make v subject of the formula the following equation
![]()
SECTION B (40 MARKS)
21. a) From the quadratic equation ax2+bx+c=0, show that 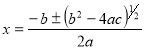
b) By using general formula of quadratic equation solve the following equation ![]()
22.John's father is 5 times older than John and John is twice as his sister Alice. In two years time the sum of their age will be 58. What is their present age?
23. a) Simplify the following by rationalizing the denominator
i) ![]()
ii) ![]()
b) Find value of P which makes the following equations perfect square
i) x2 – 8x +P=0
ii) x2 - ![]() x + P=0
x + P=0
24 a) If ![]() , evaluate:
, evaluate:
i) ![]()
ii) Find r if ![]()
b) Solve for x the following
i) 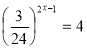
ii) ![]()
25. a) Expand the following
i) ![]()
ii) ![]()
b) Factorize the following
i) ![]()
ii)![]()
FORM TWO MATHEMATICS EXAM SERIES 7
FORM TWO MATHEMATICS EXAM SERIES 7
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256