FORM THREE MATHEMATICS EXAM SERIES 235
FORM THREE MATHEMATICS EXAM SERIES 235
 .
.FORM THREE MATHEMATICS EXAM SERIES 228
FORM THREE MATHEMATICS EXAM SERIES 228




FORM THREE MATHEMATICS EXAM SERIES 214
FORM THREE MATHEMATICS EXAM SERIES 214




FORM THREE MATHEMATICS EXAM SERIES 202
FORM THREE MATHEMATICS EXAM SERIES 202
OFFICE OF THE PRESIDENT, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT,
SECONDARY -EXAMINATION SERIES
MATHEMATICS MARCH EXAMINATION- FORM THREE
Instructions
- This paper will consist of sections A and B with a total of 14 questions
- Answer all questions in both sections A and B
- Section A will carry 60 marks and section B will carry 40 marks
- Mathematical tables/ Calculator may be used
- Write your Examination number on the top right corner of your answer booklet provided. Use R = 6400 and π= 3.14
SECTION A (60 Marks)
Answer all questions in this section
1. a) Mangoes are to be exactly divided into groups of 20, 30 or 36. What is the smallest number of mangoes required?
b) Anna was given 60,000 shillings by her mother she spent 35 percent of the money to buy shoes and 10 percent of the remaining money to buy books. How much money remained?
2. a) If log y + 21og (3x+ l) = l . Express y in terms of x
b) Given a recurring decimal 0.9666666... write it as a fraction.
3. (a) Solve the value of x if
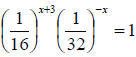
(b) If log 2 = 0.3010, without using mathematical tables, find the value of log 5
4. a) Use the number line to find the value of -3×-4
b) A village received 452009 bags of fertilizer to be distributed to 4500 Farmers. Estimate the number of bags each farmer got?
5. (a) A lecture hall has 20 rows of a seats with 100 seats in the back row, each row have 2 fewer number of seats than the row immediately behind it .How many seats are their in the lecture hall?
(b) Mabrouk invested a certain amount of money in a saving account whose interest rate was 8% compounded annually .After three year ,he got 500,000/=
(i) How much did the invest at the start.
(ii) How much did he received as interest at the end of 3 years?
6. (a) Without using tables, find the value of ![]() and simplify your answer.
and simplify your answer.
(b)The sides of a right angled Triangle are (2x + 1)Cm, (12x)Cm and (12x + 1)Cm. Find the value of x in cm if the hypotenuse is (12x + 1)cm
FORM THREE MATHEMATICS EXAM SERIES 197
FORM THREE MATHEMATICS EXAM SERIES 197
PRESIDENT’S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES,
MID TERM ONE – MARCH-2024
MATHEMATICS FORM THREE
Time: 3Hours
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions in sections A and B
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA Mathematical tables and non-programmable calculator may be used.
6. All communication devices and any unauthorized materials are not allowed in the examination room.
7. Write your examination number on every page of your answer sheet(s).
SECTION A. (40 MARKS)
Answer all questions in this section.
- (a) solve the value of x if
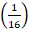 x+3
x+3 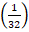 -1 =1
-1 =1
(b) If log 2 =0.0310, without mathematical time table find value of Log 5
- If a = 0.25 and b= 0.5. find the fraction
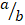 in its simplest form
in its simplest form
(b) Round off (1) 0.002098 to two significant figures
- 7.67 to the nearest whole number
- 2.77 to one decimal place
- (a) how many grams are there in 0.00912 tones
(b) the compression of 1 spring is directly proportional to the thrust T. Exerted on it . if the thrust of 4N produces a compression of 0.8, find
- The compression when the thrust is 5N
- The thrust when the compression is 0.5 cm
- The product of three terms of geometric progression (GP) is 8000. If the first term is 4 , find the second term and third term.
(b)Mahona invested a certain amount of money in serving bank whose interest was 10% compounded annually. After 32 years he got 5000 shillings.
- How much did he invest at the start
- How much did he receive as interest at the end of two years
- (a) Given that log 34 = 1.262 and log 35 =1.1465. find log 30.8
(b) the dimension of first rectangular are length 23cm and width 16 cm. a second rectangle has length 12cm and width 9cm with reasons state wether the two rectangles are similar.
- (a) solve for x in 1≤3x-2<8
(b) By using completing square method, solve equation.
![]() =4
=4
- (a) find the value of Y given that 125y+1+53y=630
(b) find the value of x given that 2log x= log 4+log (2x-3)
- (a) Given three points A (3,3) B (-3,1) C (-1,-1) and D (1,-7)
- Show that the line through A,B, And CD are perpendicular to each other
- Find equation of the line through point (-4,5) which is parrralel to BC
- (a) The fifth and the eleventh term of an arithmetic progression are 8 and -34 respectively. Find the sum of the first ten terms
(b) Prove that the interior angle of a cyclic quadrilateral is equal to the opposite interior angle
- (a) Mayele bought 3 bottles of juice of capacity 350ml and Dialo bought 1 bottle of juice of capacity 1 Litre
- Who had more juice to drink
- Bu how much more?
(b) Simplify the sum of 85% of 9861 and 3/5 of 12458. Write your answer to two significant figures.
SECTION B. 40 MARKS
- (a) in a certain research the data were summarized as shown on the table below
| Class mark | 10 | 15 | 20 | 25 | 30 | 35 |
| frequency | 3 | 2 | 10 | 5 | 4 | 1 |
By using the data above reconstruct a frequency distribution table including class interval and frequency
(b) Prove that equal chords of a circle subtends equal angles at the centre
- (a) solve for the quadratic equation x2-8x+7=0
(b) Solve for x and y if ![]()
- (a) (i) without using table . Draw the graph of
F(x)=x2+2y-4
(ii) State domain and range of f(x)
(b) A field is 10M longer than its width. The area is 7200m2 . Find its width
- (a) The product of a three terms of geometric progression G.P is 8000. If the first term is 4. Find the second term and third term
(b) Amina invested a certain amount of money in a serving bank whose interest rate was 10% compounded annually. After two years she got 5000.
- How much did she invest at the start
- How much did she receive as interest at the end of two years?
FORM THREE MATHEMATICS EXAM SERIES 166
FORM THREE MATHEMATICS EXAM SERIES 166
PRESIDENT’S OFFICE REGIONAL, ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM THREE ANNUAL EXAMINATION
041 BASIC MATHEMATICS
TIME:3 HOURS NOV, 2023
INSTRUCTION
- This paper consist of two sections A and B
- Answer all questions
- Calculators and mathematical tables may be used
- All diagram must be drawn by using pencil
- All writing must be in a blue or black ink
SECTION A (60 MARKS)
- (a)Write 490.032578 correct to
- 5 significant figure
- Thousandths
- 4 decimal places
(b)The anterior angle of a regular polygon is four times as its exterior angle. Find
- Size of each exertion angle
- Number of sides
- State name of polygon
- (a)Solve the following exponential equation
![]()
(b)Given log 52 = 0.4307 and log 53 = 0.6826
- (a)A painter placed 20m ladder against the wall of a house so that the base of the ladder is 4m away from the wall. How high does the ladder touch the wall from the ground?
(b)If ![]() Where A is an active angle find
Where A is an active angle find
- Sin A
- Cos A
- (a)If
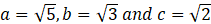 simplify
simplify 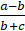
(b)Describe application of Logarithm in daily life
- (a) In following figure.
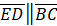 and
and 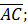 if
if 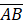 =13cm and
=13cm and 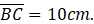 Find area of BCDE
Find area of BCDE
(b) What do the following terms mean as used in accounting
- Cash Book
- Assets
- Credit Transaction
- (a)A company bought two vans for Tshs 25,000,000/=each. If one car was sold at a profit of 18% and another was sold at a loss of 6%. In the whole transaction, there was no loss. What was profit made by the company?
(b) If the square of the hypotenuse of an isosdes right angle Triangle is 128cm2. Find the length of each side.
- (a)From the top of a tower of height 60m the angles of depression of the top and bottom of a building are observed to be 30° and 60° respectively. Find the height of the building.
(b)Three bells commerce tolling together and toil at an interval of 8, 10 and 12 seconds respectively. How many times do they together is 50minutes?
- (a) If the length of each side of a square is mix eased to 16times the area of Small Square. Find the length of one side of Original square
(b)A large rectangular garden in a park is 120m wide and 150m long. A contractor is called in to add a brick walkway to surround the garden by the same width. If the area of the walkway 2800m2 how wide is the walkway?
- (a)
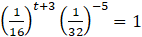 . Find the value of t
. Find the value of t
(b)Write “L” in terms of M, N and T from the formula
![]()
(c)Determine the value of x if ![]()
- (a) Let
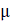 be a universal set and A and B be sub-set of
be a universal set and A and B be sub-set of 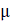 , if μ = {a, b, c, d, e, f, g, h}
, if μ = {a, b, c, d, e, f, g, h}
A = {c, g, f} and B = {b, d, h} find
- The number of sub sets of set A
- n(A'∩B)
(b)The traffic lights at three different road crossing changing after every 48 seconds, 72seconds, and 108 seconds respectively. If they change simultaneously at 7am at what time will they change simultaneously again?
SECTION B (40 Marks)
Answer all questions
- (a)The marks in Basic Mathematics terminal examination obtained by 40 students in one of secondary schools in same district were as follows.
60, 54, 48, 43, 37, 61, 43, 66, 65, 52, 37, 81, 70, 48, 63, 74, 67, 52, 48, 37, 48, 42, 43, 52, 52, 22, 27, 37, 44, 38, 29, 19, 28, 36, 42, 47, 36, 52, 50, 28.
- Prepare a frequency distribution table with class interval 10 – 19, 20 – 29, etc
- Find class that contain medium
- Find the mean
- Calculate the median
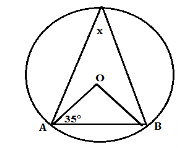
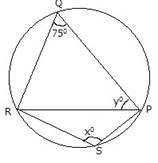
(b)Find the value of angle x in figure below, where O in the center of the circle.
- (a) Two towns P and Q on latitude 48° are 370 nautical Milles a part. Find the difference in their longitude.
(b)A regular hexagon is inscribed in a circle. If the perimeter of hexagon is 42cm. Find the radius of the circle and its area.
- (a)If
 and
and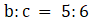 . Find
. Find 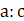 and
and 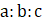
(b)From the following information given by Mbeya Co. Ltd for the year ended 31st Dec 2022.
Stock (01.01.2022) ................... Three quarter of closing
Stock (31.12.2022) .............. ![]() of Net purchases
of Net purchases
Net purchases during 2022 ................ 432.000
Gross Margin ........................... 15%
Expense .................................... 20% of Net profit
Calculate:
- Cost of good sold
- Gross profit
- Net-profit
- (a)(i) With using table of values draw the graph of
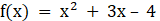
(ii) State the domain and range of f(x)
(b) Solve for x and y if
![]()
FORM THREE MATHEMATICS EXAM SERIES 151
FORM THREE MATHEMATICS EXAM SERIES 151
PRESIDENT’S OFFICE
REGIONAL, ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM THREE MID TERM EXAMINATION
041 BASIC MATHEMATICS
TIME:3 HOURS AUG, 2023
INSTRUCTION
1. This paper consist of two sections A and B
2. Answer all questions
3. Calculators and mathematical tables may be used
4. All diagram must be drawn by using pencil![]()
5. All writing must be in a blue or black ink
SECTION A (60 MARKS)
1. (a) If a=![]() write in the form of a/b where b≠0
write in the form of a/b where b≠0
(b)Three bells are set to ring at intervals of 12 minutes,15 minutes and 24 minutes. If they started together at 2:00 pm, then find at what time will the bells ring together for second time
2. (a)Find the value of X if (![]() )x+3(
)x+3(![]() )-x=1
)-x=1
(b)Solve for X if log39-1=X2-2x-5
3. (a)If ![]() = p+q√r, simplify by rationalizing the denominator and hence find the value of p, q and r
= p+q√r, simplify by rationalizing the denominator and hence find the value of p, q and r
(b)In a class of 100 students, 38 study mathematics,20 study biology and 45 study neither of two subjects by using venn diagram, find the number of students who
(i)Study both subjects
(ii)Study exactly one subject
4. (a) A straight line has a gradient of ![]() and it passes through the point (-1,2). Find
and it passes through the point (-1,2). Find
(i)Its equation
(ii)The Y-intercept
(b)Make V the subject from ![]()
![]() =
= ![]()
5. (a) a radio is bought for sh.24,000 a sold for sh. 36,000. Find the
- The profit made
- The percentage profits
(b) The operation a![]() b = (a+b)2- ab
b = (a+b)2- ab
Find the value
- 3
 2
2 - 9
 -
-
6. (a) The variable V varies directly as the square of X and inversely as Y. Find V when X =5 and Y=2, When V =18, X=3 and Y =4.
(b) Water from a tap gets into a tank at a rate of 20 litres per minutes. How long will it take to fill a tank that is 10,000 litres. Give your answer in hours and minutes.
7. (a) Find the first term and common difference of an arithmetic progression whose 5th term is 21 and 8th term is 30.
(b) The products of three terms of a geometric progression (GP) is 8000. If the first term is 4. Find the second term and the third term.
8. (a) How many grams are there 0.00912 tones?
(b) A ladder 15cm long leans against of vertical wall so that angles make with the horizontal ground is two times that makes vertical wall. Calculate how far up the wall does the ladder reaches?
9. (a) Basil has to share eighty books with his daughters Rose and Nancy. He decided that for every two books Nancy gets, Rose gets three books and he gets five books. Find the number of books each gets.
(b) Solve by elimination method 2x – y = 1
x + y = 1
10. (a) Solve the quadratic equation x2-8x+7=0 by completing the square
(b) A field is 10m longer than its wide. The area is 7200m2. What is the width?
SECTION B (40 MARKS)
11. The table below represents score of 100 students in geography test
| Marks ( | 40 - 49 | 50 - 59 | 60 - 69 | 70 - 79 | 80 - 89 | 90 – 99 |
| Frequency | 7 | 13 | 36 | 30 | X | 4 |
- Determine the value of X
(b) By using assumed A=74.5, determine mean
(c) Find mode
(d) Find median
12. (a) Kwembe went to the market with 3000Tsh to buy oranges and mangoes. He bought 20 oranges and 5 mangoes. If Grace went to the same market with 2000Tsh and bought 10 oranges and 5 mangoes. What is the price of one mango and one orange?
(b) Mchilo invested a certain amount of money in a saving Bank whose interest rate was 10![]() compound annually. After two years he got 5000 shillings.
compound annually. After two years he got 5000 shillings.
(i) How much did he invest at the start?
(ii) How much did he receive as interest at the end of two years?
13. (a) Given a function f(x)=x2-2x-3. Find
(i) Line of symmetry
(ii) The turning point
(iii) Express f(x) in the form of a(x+b)2+c where a,b and c are real numbers
(b) If f(x) is the function such that
F(x)=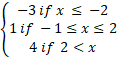
(i) Sketch the graph of f(x)
(ii) State the domain and range of f(x)
(iii) Find the value of f(100)
14. MRS CHENI started a business on 16thMarch 2023 with capital in cash 2,066,000
March 17 Bought goods for cash 1,000,00/-
19 Bought shelves for cash 110,000/-
20 Sold goods for cash 900,000/-
21 Purchased goods for cash 800,000/-
22 Sold goods for cash 1,400,000/-
26 Paid rent 300,000/-
(i) Record the above transaction in cash account
(ii) Extract a trial balance
1
FORM THREE MATHEMATICS EXAM SERIES 147
FORM THREE MATHEMATICS EXAM SERIES 147
PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM THREE
TERMINAL EXAMS MAY – 2023
041
TIME: 3HOURS
INSTRUCTION
- This paper consists of two sections A and B with total of fourteen (14) questions
- Answer all questions
- Programmable calculators, phones and any other unauthorized materials are not allowed in examination room
- Write your examination on every page of your answer sheet provided
- All diagrams must be drawn in pencils
- All writings must be in black/blue ink
SECTION A. 60 MARKS
1. (a) Equal squares as large as possible are drawn on a rectangular board measuring 54cm by 78cm. Find the largest size of the squares.
(b) (i) Express 2.7?9? as a fraction in the form a/b where a and b are integers and b≠0
(ii)Arrange 2/5, 5/8 ,48% and 0.6 in ascending order
(iii) Show on the number line the solution set of the inequality
?2x+1?>3
2. (a) i. If x2 +ax +4=0 is a perfect square . Find the value of a
ii. If x2 +bx +c =(x-3)(x+2) determine the values of b and c
iii. Solve the following quadratic equation by complete the square method x2 + 6x +7=0
(b) i. Solve 3 - of (6x+9) = 5-2x
ii. If U*V =UV+V, Find x given that (x*2)*5=60
3. (a) Rectangular table top is 2m long. If the area of the rectangular table top is
3.96m2. find its width
(b) i. Solve the following simultaneous equations
2x+3y=5
4x+23=5y
ii. If Fatuma is 4 years less than Bakari and 3 times Fatuma's age is equal to 2 times Bakari's age. What are their ages ?
4. (a) If find the value of t
(b)Write “L” in terms of M, N and T from the formula
(c) Determine the value of x if
5. (a)If the 5th term of an arithmetic progression is 23 and the 12th term is 37, find the first tem and the common difference.
(b) In how many years would one double one’s investment if Tshs 2500 is invested at 8% compounded semi –annually.
6. (a) If y varies inversely as and x is multiplied by n. What is the ratio of the first y to the second y?
(b) The headmaster has enough food to last for his 600 students for 20 days from tomorrow. If 120 students leave the school today for UMISSETA game, how long will the food last?
7. (a) The sum of the first six terms of an A.P is 72 and the second term is seven times the fifth term.
- Find the first term and the common difference
- Find the sum of the first ten terms
(b) Find the sum of the first four terms of a geometric progression which has a first term of 1 and a common ratio of
8. (a) The gradient of line L1is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
(b) The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
9. (a) Find the value of
Without using mathematical tables.
(b) Calculate the angles of a triangle which has sides of lengths 4m, 5m and 7m
10. (a). Given that x2 –y2 = 27 and x + y = 9 find the value of xy
(b). Solve the equation 2x2 – 3x – 5 = 0 by completing the square.
SECTION B (40 Marks)
Answer all questions
11. (a) The number of workers absent in 52 working days is given in a cumulative frequency table below
| No.of absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 - 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find
- Percentage of workers who are absent at least for 20 days
- Median
(b) Find the angle x in the figure below
12. (a) A ship sails from point A (40) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and
(give your answer in nearest degree)
(b) VABCD is a pyramid with VA=VB=VC=VD=5cm and ABCD is a square base of sides 4cm each. Assume that the centre of the base is at point N. Find
(i) The angle between VA and the base ABCD
(ii) The volume of the pyramid
13. (a) If tan A = , where A is an obtuse angle,
Find (i). Cos A + Sin A (ii). – Cos2 A – Sin2 A
(b) A and B are two points on the ground level and both lie west of flagstaff. The angle of elevation of the top of the flagstaff from A is 560 and from B is 430. If B is 28m from the foot of the flagstaff. How far apart are the points A and B?
14. (a)The marks in basic Mathematics terminal Examination obtained by 40 students in one of the secondary school in Katavi were as follows;
60, 54, 48, 43, 37 61, 43, 66, 65, 52, 37, 81, 70, 48, 63, 74, 67, 52, 48, 37, 48 42, 43, 52, 52, 22, 27, 37,44 38, 29, 19, 28 36, 42, 47, 36, 52, 50, 28.
- Prepare a frequency distribution table with class intervals 10 – 19, 20 – 29, etc.
- Find the class which contain the median
- Find the mean
- Calculate the median.
(b) A field is 10m longer than its width. The area is 7,200m2. What is the width?
FORM THREE MATHEMATICS EXAM SERIES 135
FORM THREE MATHEMATICS EXAM SERIES 135
PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM THREE
MID-TERM EXAMS MARCH – 2023
041
Time: 3Hours
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in sections A and B
- Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answer for each question must be shown clearly
- NECTA mathematical tables and non-programmable calculator may be used
- All communication devices and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s)
SECTION A: (60 Marks)
Answer all questions from this section
1. (a)The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7am at what time do they change simultaneously again?
(b) If x = 0.567567567 and Y = 0.83 by Converting these decimal to fractions, find the exact value of
2. (a) If Find the value of t
(b)Write ‘L’ in terms of M1 N and T from the formula
(c)Determine the value of x if
3. (a)If the 5th term of A.P is 23 and 12th term is 37 find the first term and common difference
(b)How many years would one double one’s investment if Tsh 2500 is invested at 8% compounded semi-annually
4. (a)Find value of x and y if
(b)Let U be universal set and A and B be the subsets of U where
U = {a, b, c, d, e, f, g, h} A={c, g, f} and B= {b, d, h}
(i) Find the number of sub sets of set A'
(ii) Find n (A'n B')
(iii) If an element is picked at random from universal set (U), find the probability that it is an element of set B
5. (a)The coordinate of P, Q and R are (2, m), (-3, 1) and (6, n) respectively. If the length of PQ is units and midpoint of QR is
find possible value of m and n
(b)The gradient of line L, is – 2, another line L2 is perpendicular to L1 and passes through (-3, -2) what is the equation of L2
6.
(a)If = 17cm,
=8cm,
= 12cm, and angle ABD = 90°. Calculate the length
(b)(i) Given where
and
are the sides of Triangle ABT and
are sides of triangle KLC. What does this information imply?
(ii)A regular Hexagon is inscribed in a circle, if the perimeter of the hexagon is 42cm, find the radius of circle and its area.
7. (a)Rationalize the denominator of
(b)Without using mathematical tables find value of 3 log5 + 5log2 – 2log2
8. (a)Solve for x in the inequality 3x – 4 ≥ x + 16
(b)Solve the following pairs of simultaneous equation by elimination method
9. (a)The sum of first six terms of an AP is 72 and the second term is seven times the fifth term
(i) Find the first term and the common difference
(ii) Find the sum of first ten terms
(b)Find the sum of the first four terms of a geometric progression which has a first term of 1 and common ration of
10. (a)The gradient of line L1 is -2, another line L2 is perpendicular to L1 and Passes through point (-3, -2) what is the equation of L2?
(b)The area of the triangle ABC is 140cm2, AB=20, AC=14cm find the angle BAC
SECTION B (40 Marks)
Answer all questions
11. (a)The number of workers absent in 52 working days is given in a cumulative frequency table below
| No. of Absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 – 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find.
(i) Percentage of Workers who are at least for 20 days
(ii) Median
(b)Find the angle x in figure below
12. (a)The function f is defined as follows
- Sketch graph of f(x)
- Determine Domain of f(x)
- Determine the range of the function
(b)In a triangle ABC the ratio of angle is A: B: C = 2:3:7 the length of shortest side = 5cm. Find the length of longest side.
13. (a)Find the first term and common difference of an AP whose 5th term is 21 and 8th term is 30
(b)Find the 10th term of a sequence whose first three consecutive terms are 5, 15 and 45. Leave your answer in exponents
14. (a)Mr.Ogango from Kenya visited Tanzania. He had 5,000 Kshs and wanted to change the money into LIS dollar. If 1 Us dollar was equivalent to 2500 Tanzania shillings (Tshs) AND Ksh 1 was equivalent to Tshs 20 how much Us dollars did he get.
(b)A gardene has found that the time cut grass on a square field varies directly on the square of its length (L) and inversely as the number of men (m) doing that job. If 5 men cut grass on field of size 50m in 3 hours, how many more men are required to cut grass on a field of side 100m in 5 hours. Assume
FORM THREE MATHEMATICS EXAM SERIES 125
FORM THREE MATHEMATICS EXAM SERIES 125
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
MATHS ANNUAL EXAMINATIONS
FORM THREE-2022
INSTRUCTIONS
- This paper consists of section A and B with a total of fourteen (14) questions.
- Answer all questions in both sections
- Each question in section A carries six (6) marks while each question in section B carries ten (10) marks
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables or non-programmable scientific calculator and graph papers may be used unless otherwise stated
- You are advised to spend no more than two (20 hours on section A
- All communication devices and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number on every page of your booklet(s)
SECTION A (60 MARKS)
Answer all questions in this section.
- (a) At exactly 7:00a.m, two buses leave the bus terminal. Thereafter, every 40 and 70 minutes, a bus leaves the terminal. Find the time busses will leave the terminal together.
(b)(i) Estimate the value of ![]()
(ii)Simplify the ratio of a tob, given that ![]() and b=
and b=![]() to its lowest form.
to its lowest form.
- (a) Solve for x in the equation
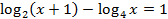
(b) If 3x – y=4, What is the value of ![]()
- A bag contains 6 red balls and 8 blue balls. A random selection of balls from the bag is performed. If one ball is selected from the bag and then replaced before selecting the second ball:
- Draw a tree diagram showing all the possible outcomes and their corresponding probabilities
- Find the probability of selecting
- Balls of different colours
- Balls of the same colour
- (a)Three consecutive vertices of parallelogram are at A(-1, 2), B(5, 1), C(6, 5), and
D(x, y), Find the coordinate of vertex D.
(b) Two towns P and Q are 30km apart, Q being due East of P. Town R is situated at a bearing of 150° from P and 240° from Q. calculate the distance RQ
- (a)P and Q are markers on the banks of a canal which has parallel sides. R and S are telegraph poles which are directly opposite each other. PQ=30m and QR=100m. When Mr. Ates walked 20m from P directly away from the bank, he reached a point T such that T, Q and S lined up. How wide is the canal?
(b)In a triangle ABC, angle ABC=50° and point X lies on ![]() such that
such that ![]() with the aid of a diagram, calculate
with the aid of a diagram, calculate ![]()
- (a)An English family on holiday in France exchanged 450 for euros when the exchange rate was 1.41 euros to the pound. They spent 500 euros and then exchanged the rest back into pounds, by which time the exchange rate had become 1.46 euros to the pound. How much did the holiday cost? (Give your answer in pounds.
- The following balance sheet relates to Mr. Max Malipo, a trader, as at 31st December 2020
MR. MAX MALIPO
| PARTICULARS | AMOUNT | PARTICULARS | AMAUNT | ||
| CAPITAL Add: Net Profit
Less: Drawings
LIABILITIES Creditors Salaries Accrued Tel. Outstanding | 179,000 30,280 |
191,280
7,000 5,000 220 | ASSETS Furniture Machinery Debtors Cash at Bank Rates Prepaid Closing Stock |
|
40,000 30,000 10,000 3,000 500 120,000
|
| 209,280 18,000 | |||||
|
| |||||
| 203,500 | 203,500 | ||||
Use the information given in the balance sheet above to find:
- Total Fixed Assets
- Total Current Assets
- Total Current Liabilities
- Working Capital
- (a)Mr. Cathbert starts an employment with a monthly salary of 340,000/= Tshs and receives an increment of 12,000/= Tsh every year.
- What will be his salary in the fourteenth year of employment?
- After how long would he be earning 592,000 Tsh per month?
(b)The sum of the first two terms of a geometric progression is 27 whereas the sum of the 2nd and 3rd term of the same progression is 54. Find the first term and the common ratio.
- (a)At a point 200m from the foot of a tower on a level road, the angle of elevation of the top of the tower is 58°.
- Represent this information diagrammatically,
- Find the height of the tower.
(b)A rectangular frame ABCD, 48cm by 55cm, is made from wire. The diagonals of the frame are also made from wire.
Calculate the total length of wire needed to make the frame and the diagonals.
- (a)Find the values of m and n in system of linear equations
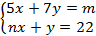
(b)Find the values of a andb if (ax + 5) (bx + 4) = 21x2 + 43x + 20.
SECTION B (40 Marks)
Answer all questions in this section
- (a)The table below shows the distribution of marks scored by 45 students in Physics examination
| Marks (in %) | 99 – 89 | 88 – 78 | 77 – 67 | 66 – 56 | 55 – 45 |
| Number of students | 2 | 5 | 20 | 11 | 7 |
- Determine the median class of marks
- Compute the mean mark
- Draw the histogram and hence use it to estimate the mark scored by many students
(b) ![]() are secants that intersect at A in the figure below. Given that chords
are secants that intersect at A in the figure below. Given that chords ![]() Find the angles x and y.
Find the angles x and y.
- (a)A circular tank has a base of 53-metre radius and height of 12 metres. If the tank is a half full of water, what is the volume of water in a tank? Give your answer in litres (1 cubic metre = 1000 litres)
(b)Mr. Paul went to buy a car. He wanted to buy a car that has not covered more than 2,500 kilometres (not much used). If he found only one car in the market which travelled from Nairobi (56°N, 40°E) to Dar-es-Salaam (26°N, 40°E). What can you advice Mr.Paul according to his need? (Use radius of the Earth, RE= 6370km)
- (a)Find value of K if the matrix
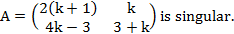
(b)Use inverse matrix method to solve for x and y in the following pair of equations of straight lines: ![]()
(c) A linear transformation T maps ![]() .
.
Find
- The transformation matrix T
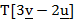
- (a)Find the role of the following is solving linear programming problems:
- Non-negativity constraints
- Feasible region
- Objective function
(b) MzeeMalengo has 240 acres of land which he wants to plant maize and oats. For each acre of maize planted he will profit 400,000/= Tsh, and for each acre of oats planted he will profit 300,000/= Tsh. However, maize takes 2 hours to harvest, while oats require 1 hour harvesting, and he has only 320 hours available for harvesting. How many acres of each crop should he plant in order to maximize profits?
FORM THREE MATHEMATICS EXAM SERIES 113
FORM THREE MATHEMATICS EXAM SERIES 113
THE UNITED REPUBLIC OF TANZANIA PRESIDENT'S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM THREE ANNUAL EXAMINATION
041 BASIC MATHEMATICS
Time 3:00 Hours Year: 2022
INSTRUCTIONS
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions
- Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- Mathematical tables and non-programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room
- Where necessary, use the following constants
- Pie,
 =3.142
=3.142 - Radius of the earth, Re =6400km.
SECTION A: (60 MARKS)
Answer all questions from this section
1. (a)The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m at what time they change simultaneously again?
(b) If x = 0.567567567… and y = 0.8![]() by converting these decimals to fractions, find the exact value of
by converting these decimals to fractions, find the exact value of ![]()
2. (a) If ![]() find the value of t
find the value of t
(b)Write “L” in terms of M, N and T from the formula ![]()
(c) Determine the value of x if ![]()
3. (a)Let ![]() be a universal set and A and B be the subsets of
be a universal set and A and B be the subsets of ![]()
A= {c, g, f} and B= {b, d, h} find
(b) Given that A= {x : 0 ≤ x ≤ 8}
B = {x : 3 ≤ x ≤ 8}
where x is an integer, in the same form, represent in a Venn diagram
- A u B
- A n B
and hence find the elements in each set.
4. (a) Find the slope of a straight line which passes through points A (0, a) and B(3a,0)
(b) The co-ordinates of the square PQRS are given by P(1, 4), Q(3, 4), R(3, 2), and S(1, 2). Write the co-ordinates of the image of the square P’Q’R’S’ under reflection in the x-axis.
5. (a) Given ![]() where
where ![]() are the sides of the triangle ABT and
are the sides of the triangle ABT and ![]() Are sides of the triangle KLC. What does this information imply?
Are sides of the triangle KLC. What does this information imply?
(b) Calculate the area of the following figure, if 0 is the centre of the circle and OABC is a square.
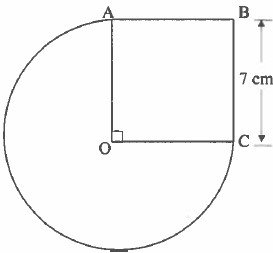
6. (a)Twelve people can dig a trench in 15 days for 8 hours daily. How long can they take to finish the same work, working for 10 hours daily?
(b)A variable V varies jointly as the variable A and h. when A=63 and h=4, v=84.
Find;
- V when A=9 and h=7
- A when V=4.5 and h=0.5
7. (a)If a:b=2:3 and b:c=5:6. Find a:c and a:b:c
(b) PQR is an isosceles triangle whereby PQ =PR and QS = SR. If S is a point between Q and R prove that Δ PQS ≡ ΔPRS
8. (a)If the 5th term of an arithmetic progression is 23 and the 12th term is 37, find the first tem and the common difference.
(b) In how many years would one double one’s investment if Tshs 2500 is invested at 8% compounded semi –annually.
9. (a) Given that
![]()
Find :
(i)![]()
(ii)![]()
(b) A and B are two points on the ground level and both lie West of flagstaff. The angles of elevation of the top of the flagstaff from A is 56° and from B is 43°. If B is 28m from the foot of the flagstaff. How far apart are the point A and B?
10. (a)Solve for the quadratic equation x2 – 8x + 7=0
(b)Solve for x and y if ![]()
SECTION B (40 MARKS)
Answer all questions from this section
11.The marks in basic Mathematics terminal Examination obtained by 40 students in one of the secondary school in Katavi were as follows;
60, 54, 48, 43, 37 61, 43, 66, 65, 52, 37, 81, 70, 48, 63, 74, 67, 52, 48, 37, 48 42, 43, 52, 52, 22, 27, 37,44 38, 29, 19, 28 36, 42, 47, 36, 52, 50, 28.
- Prepare a frequency distribution table with class intervals 10 – 19, 20 – 29, etc.
- Find the class which contain the median
- Find the mean
- Calculate the median.
12. (a) From the following information given by Mbeya Co.ltd for the year ended 31st December 2021.
Stock (01.01.2021) ………………………….Three quarter of the closing stock
Stock (31.12.2021) ………………………… ![]() of net purchase
of net purchase
Net purchases during 2021 …………………. 432,000.
Gross margin …………………………. 15%
Expenses ……………………………… 20% of Net profit
Calculate;
- Cost of goods sold
- Gross profit
- Net profit
(b) State Three uses of the trial balance
13. (a) Find the value of angle x in the figure below, where O is the centre of the circle
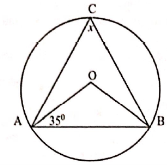
(b)Two places P and Q both on the parallel of latitude 26°N differ in longitudes by 40°, find the distance between them along their parallel of latitude.
14. Given
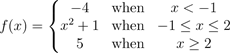
(i) Sketch the graph of f(x).
(ii) State the domain and range of f(x) .
(iii) Is f(x) a one-to-one function? Give reason(s).
FORM THREE MATHEMATICS EXAM SERIES 103
FORM THREE MATHEMATICS EXAM SERIES 103
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM THREE BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 3:00 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorized materials are not allowed in the examination room.
SECTION A
ANSWER ALL QUESTIONS
1. (a) Write ![]() as a mixed fraction
as a mixed fraction
(b)If ![]() and
and ![]() find x + y to 3-significant figure
find x + y to 3-significant figure
2. (a)Find ![]()
(b) A farmer sold a quarter of his maize harvest and gave one third of the remaining to his relatives.
If the farmer remained with 25 bags. If maize, how many bags of maize did the farmer harvest?
3. (a)Factorize (i) ![]()
(ii) ![]()
(b)Simplify ![]()
(c)Solve for x: ![]()
4. (a)Solve for x: (i) ![]()
(ii) ![]()
(b)If log3 = 0.4771 and log2 = 0.3010
Find:
(i)![]()
(ii)![]() Without using tables.
Without using tables.
5. Solve the following simultaneous equations
6. Given the universal
Set ![]() and
and ![]()
- Represent the above information in a Venn-diagram and use it to find elements of
![]()
- Show that
![]()
7. (a)Marium served Tshs 6 million in a serving account Bank where interest rate was 10% compounded annually. Find the amount in mariam’s account after 5years.
(b)In how many years would one’s investment double if 100,000/= is invested at 10% compounded semi-annually?
8. (a) Factorize:
![]()
![]()
(b) Given that
AB=EC
![]()
![]()
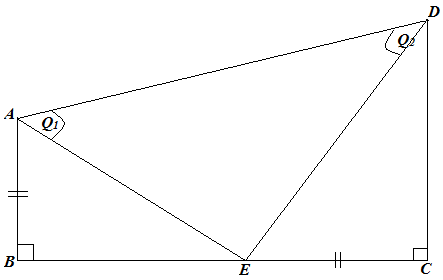
- Show that EA=ED
- Prove that
![]() and state the postulate out of (SSS, AAS, SAS, RHS)
and state the postulate out of (SSS, AAS, SAS, RHS)
9. (a)The ratio of the areas of two similar polygons is 144:225. If the length of a side of the smaller polygon is 60cm, find the length of the larger polygon
(b)
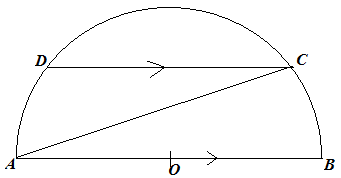
Given that
- DC//AB
- AOB is diameter
![]()
Find an expression in terms of x
![]()
10. In a series between the integers 3 and 102. Find the sum of
- Even numbers (ii) Odd numbers
(b) A bacteria produces 10 bacteria after every minute and each of the 10 bacteria produces, 10 bacteria after every minute and so
- Form a sequence of number of bacteria produced after 1,2,3 and 4 minutes
- If the frequency is to form a series, what is the name of the series?
- Find the sum of bacteria produced after one hour.
SECTION B (Answer All Questions)
11. The table below represents the scores in general cleanliness of 30 students
| SCORE x | FREQ f | fx |
| 1 | M |
|
| 2 | 2m |
|
| 3 | 10 |
|
| 4 | 8 |
|
| 5 | 3 |
|
|
| ?f | ?fx |
- Find the value of m
- Complete the table and find ?f, ?fx
- Find the mean (average) score
- Find the mode
- Construct an ogive and use it to estivate the median
12. Given the function f(x) = x2-8x + 12
- Find the x and y-intercepts
- Using (a) determine the axis of symmetry of f(x)
- Using (b) determine the coordinates of the minimum point
- Using (a) (b) and (c) sketch the graph of f(x)
- From the graph find
- Domain (ii)Range
- Construct a suitable line and sketch it on the same axes to find solution of the equation; x2 -10x + 16=0
13. (a)An aero plane fires from Tabora (5°S, 33°E) to Tanga (5°S, 39°E) at 332 km/her. Along parallel latitudes. If it leaves Tabora at 3 p.m., find the time of arrival at Tanga air-port
(b)Another plane flying at 595 km/hr leaves Dsm (7°S,39°E) at 8:00a.m it Addis Ababa (9°N, 39°E) (parallel longitude)
(Radius of the earth R![]() 6370km)
6370km)
14. (a) The volume V of a given mass of gas varies directly as the absolute temperature T and inversely as the pressure P
If V=450 and T= 288 when P=825, find V when T=320 and P = 720
(b) In the figure below, BD is a tangent to the circle having the centre O .
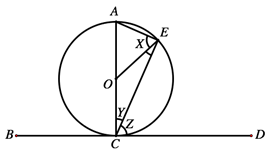
Given that angle OEC = 28°, find the values of angles marked X , Y and Z .
FORM THREE MATHEMATICS EXAM SERIES 92
FORM THREE MATHEMATICS EXAM SERIES 92
OFFICE OF THE PRESIDENT, MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
TERMINAL EXAMINATIONS- MAY 2022
FORM THREE BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a)If a*b=b (a2 – 2b) Find (i) 3*2 (ii) n if 4*n=0
(b)Given
![]()
![]()
2.A and B are two sets such that
-
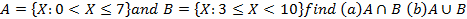
- In a class of 30 students 17 participate in English debate, 12 participate in English debate and sports. If every student is required to participate in at least one of the two subjects. Find the number of students who participate in
(i) English debate only (ii) Sports only
3.(a)If ![]()
(b)Express as single logarithm the expression ![]()
4.Rewrite without absolute value ![]() and sketch a graph of the resulting inequality
and sketch a graph of the resulting inequality
5.(a)The second term of an A.P is 2 and the sixth term is 14. Find
- The first term
- The common difference
(b)A function is defined by ![]() . Find
. Find
(i) The inverse ![]() of this function (ii)
of this function (ii)![]()
6.Given that ![]() find value of
find value of
- Cos A
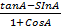
7.Fine the remainder when ![]() is divided by x + 1 and hence solve the equation
is divided by x + 1 and hence solve the equation ![]()
8.If ![]() evaluate
evaluate
- Correct to 3 decimal places
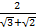
- Simplify
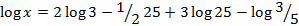
- Given
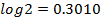 and
and 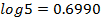 find
find 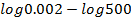
9.
- Given that
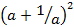 = find value of
= find value of 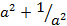
- Make q the subject of the equation
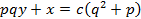
- Solve the equation
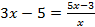 by factorization
by factorization
10. A line passes through point A (3,5) and B (8, K) has a slope of -2. Find the;
- Value of K
- The equations of line
SECTION B
11.(a)Mpira club has the following number of goals scored against them, 0,1,0,2,9,0,1,2,1, what is the mean number of goals scored against them?
(b)The table below shows the masses of 100 students to the nearest kg
| Mass kg | 60-62 | 63-65 | 66-68 | 69-71 | 72-74 |
| Frequency | 5 | 18 | 42 | 27 | 8 |
- Determine the mean of the masses
- Calculate the mode
- Draw a cumulative frequency (give) curve and use it to determine the median of the masses
12.(a)(i) Find the distance between Mbeya (9°S.33°E) and Tabora (5°S,33°E) in km
(b)An airplane takes off from Tabora (5°S,33°E) to Tanga (5°S,39°E) at a speed of 332 kmh-1 if it leaves Tabora at 3:00pm, at what time will it arrive at Tanga airport?
13.Musa started business on 1st June, 1999 with Tshs 6000/= as capital
June 01 Bought goods cash 3000/=
June 02 Paid office cleaners 20/=
June 03 Sold all goods for cash 3400/=
June 05 Purchased goods for cash 2000/=
June 08 Paid carriage on goods sold 40/=
June 10 sold goods for cash 3000/=
June 15 paid wages 100/=
- Enter these transactions in cash book
- Bring down the balance at the end of June
14. A house and flag post are on the ground. From an open window in a house 6m, above the ground, Abdulrazaq finds that the angle of elevation of the top of the flag post is 35° and the angle of depression of the bottom of the flag post is 20°.
15.(a) Draw the graph of ![]() taking the value of x in the interval
taking the value of x in the interval ![]()
(b)State the running point of the graph and state whether it is a maximum or a minimum.
(c)Solve the equation ![]()
(d)Use a suitable straight line, solve the equation ![]()
16. (a). Box A contains 8 items of which 3 are defective and box B contains 5 items of which 2 are defective. An item is drawn at randomly from each box. What is the probability that?
- Both items are non-defective?
- One item is defective and one item is not defective
(b)The radii of trastrom of a right cicular cone are 10cm and 7cm. If the height of this trastrom is 6cm. What will be the height of the original cone?
(c)If ![]()
- Find an expression for
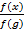
- Find the simplified algebraic expression for f(x-1)
FORM THREE MATHEMATICS EXAM SERIES 88
FORM THREE MATHEMATICS EXAM SERIES 88
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM 3 BASIC MATHEMATICS
SECTION A (60 MARKS)
Answer ALL questions from this section
1(a) Write 0.007357 correct to three significant figures
(b)Express ![]() inform
inform ![]() where
where ![]()
(c)Simplify ![]() hence write your answer in percentage.
hence write your answer in percentage.
2.(a)Solve for x in the following equation ![]()
(b)Rationalize the denominator ![]()
3(a)In a school of 200 students 90like mangoes, 70 like oranges and 50 like Apples; 26 like oranges and mangoes, 20like oranges and apples, 16like Apples and mangoes while 10 like all three fruits.
Represent this information in a well labeled Venn diagram
How many students do not like mangoes?
(b)If ![]() , Find b in terms of A and C
, Find b in terms of A and C
4. Use the graph below, then find;
Gradient
Equation of the line in the form of y=mx + c
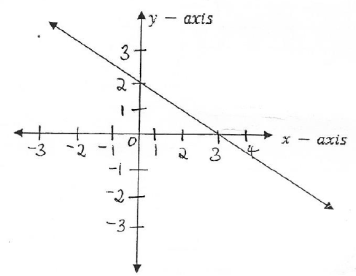
5.(a)ABC is an isosceles triangle in which![]() and
and ![]() are equal and if D is the mid-point of BC.
are equal and if D is the mid-point of BC.
Prove that ![]()
(b)A regular polygon has an exterior angle of 72° find
- The size of the interior angle
- How many sides does this polygon have?
6.(a) If y varies directly as x2 and inversely as ![]() when x=8, y=16 and z=25.
when x=8, y=16 and z=25.
Find y when x=5 and z=9
(b)Sixty people working 8 hours a day take 4 days to cultivate a village farm. How long will it take twenty people to cultivate the same farm if they work 15 hours a day?
7(a)Three people share a property in a ratio 2:x:y. It is known that y=x +2, if the largest shareholder had shs 780,000/= in monetary terms, find the value of this property.
(b)Mr.Mayube of Makole village shop made 60% loss by selling a bag of sugar for Shs. 80,000.00. What would be his percentage profit if he sold the bag of sugar for Shs 240,000.00?
8(a)Write down the next two terms in the sequence; ![]()
(b)The first four terms of an A.P are 2,(m – n), (2m + n + 7 and (m – 3n) respectively where m and n are constants. Find the values of constant m and n
9(a)Given that Tan A=2.4 and A is an acute angle. Find in the simplified form the value of ![]()
(b)From the top of a wall 8.8m above horizontal ground, the angle of depression of a stone lying on the ground 31°. Calculate the distance of the stone from the foot of the wall.
10(a)Find the factors ![]() and hence use it to solve
and hence use it to solve ![]()
(b)The operation x*y denotes the number. Find the value of x if x*4=x*3
SECTION B –(40 MARKS)
Answer any four (4) questions from this section
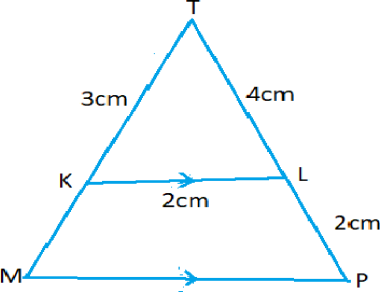
11.(a)In the following figure ![]() shorter than
shorter than ![]() . Find the length of
. Find the length of ![]()
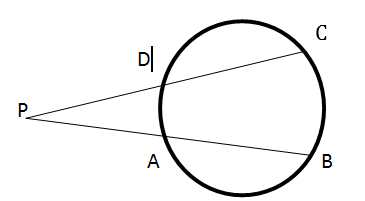
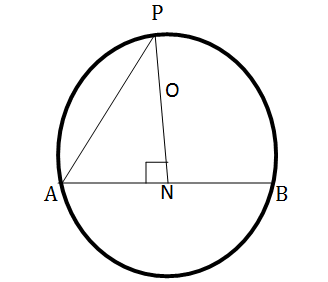
(b)In figure below O in the center of the circle. AB=6cm and ON=4cm show that ![]()
12. The score of 50 candidates a mathematics examination were recorded as shown below.
26, 17, 42, 40, 40, 74, 26, 34, 34, 47, 52, 42, 69, 52, 43
67, 38, 52, 24, 34, 48, 73, 64, 55, 43, 67, 38, 56, 18, 53, 26
62, 32, 78, 17, 45, 34, 54, 24, 36, 34, 18, 48, 52, 73, 37, 64, 45, 54, 37
- Prepare a frequency distribution table with class mark 17, 22, 27 …………
- Draw histogram and use it to estimate mode
- Calculate mean, using assumed mean of 52
13.(a)Find the distance between A(20°N, 135°E) and B (35°N, 135°E) in
(i)Nautical miles (ii) Kilometer
(b)A ship sails from P(0°, 30°W) to Q(10°N, 30°W) at 15 knots. If it leaves P at 8:00am on Tuesday when will reach Q?
14.You are required to use the trial balance below to prepare trading, profit and loss Account and extract the balance sheet of Mwanahela as at 31-12-2012
| S/NO | NAME OF ACCOUNT | DR | CR |
| Cash | 1,907,000 | ||
| Capital | 2675000 | ||
| Purchases | 2267000 | ||
| Rent | 114000 | ||
| Furniture | 305000 | ||
| Shelves | 270000 | ||
| Sales | 2309000 | ||
| Salary | 67000 | ||
| Wages | 54000 | ||
| 4984000 | 4984000 |
15.(a)The sum of the first three terms of a geometric progression is 19 and their product is 216. Find the terms
(b)The third term of an arithmetic progression 9 and the common difference in 2. Find the sum of the first 20terms.
(c)If p, q and r are successive terms of a geometric progression. Find the value of q in terms of
p and r
16.Given that 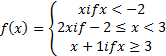
- Sketch the graph of f(x)
- State the domain and range of f(x)
- Find f(-5), f(10), f(3?) and f(0)
- Is f(x) one to one to one function?
1
FORM THREE MATHEMATICS EXAM SERIES 81
FORM THREE MATHEMATICS EXAM SERIES 81
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT AUTHORITY
BASIC MATHEMATICS EXAMINATIONS- AUG 2021
FORM THREE
TIME: 3:00HRS
INSTRUCTIONS
- This paper consists of Sections A and II
- Answer ALL questions in both sections
- Mathematical table and graph paper may be used unless otherwise stated.
- Write your Examination Number on every page of your answer sheet(s) provided.
SECTION A (60MARKS)
- (a) A school trip of 32 people went to a tour which costs a transport fee of 580/= each person. What was the approximate total transport cost?
b) Rajabu is making some small metal rods.He has three peaces of metals of length 432cm, 648cm,540cm.What is the largest length of a rod he can make if the rods have the same length and no metal is wasted.
- (a) Without using mathematical table simplify √63+√72
√32+√28
(b)Find the value of x in log( - 1) + 2 = log(3 + 2) + log 25
- a)(i) List all the subsets of the following set A = {3, 6, 8}
( ii) Work out the number of subsets in a set containing 6 elements.
b) In a class of 45 students, 19 study commerce but not physics, 16 study physics but not commerce and 3 studies neither commerce nor physics, find the number of students who study (i) Physics or commerce (ii) Both subjects
- (a) The line joining (2,-3) and (k,5) has a gradient -2, find k
b) ?PQR is such that PQPR and PQ:QR is equal to 3:4.If the perimeter of the triangle is 60cm. Calculate the value of QR.
- (a) Calculate to 1 decimal place the area of an equilateral triangle of side 10cm.
(b) In the figure below find MK and MP
- (a) A man is paid 6000/= for 8 hours work (i) What is his rate of pay? (ii) At this rate how long must he work to receive 30,000/=
b) In working for 10 hours a day, 12 men can do a certain piece of work in 6 days. For how many hours a day must 20 men work in order to do the same amount of work in 14 days?
- a) By selling an article at Tsh 225,000 shopkeeper makes a loss of 10%.At what price must the shopkeeper sell the article in order to get a profit of 10%?
b) Find the total amount of money received if Tsh 800,000 is deposited in a bank at the rate of 9% compounded semi anually in one year.
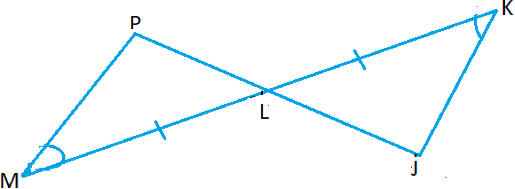
| ~ =, | L is a mid point of KM .Prove that L ≡ L |
(b) Given the angles A? C = 2x+30° and C? D = (x+15)°. If two angles are complementary find the value of x and the size of each angle
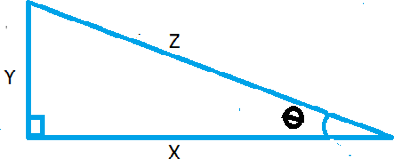
- (a) Given the right angled triangle below with sides marked x , y , z ,
Prove that cos2 + sin2=1
b) A pole 7.45m high casts a Shadow 4.05m long on horizontal ground. Find the angle of elevation of the sun.
10. (a) Expand the expression (ax + c) (bx – d)
(b) A boy bought some packets of biscuits for 120/=.If the biscuits had been 3/= a packet cheaper he would have received 2 more packets for his money. How many packets did he buy?
SECTION B (40MARKS)
11. In a mathematics Examination the following marks were obtained:
27 57 57 40 70 48 59 60 42 44 47 44 44 59 35 48 43 52 36 48 Group the marks in class interval of 20-29, 30 -39 , . . . Then
- Construct the frequency distribution table
- Calculate the mean marks by using assumed mean method (Take A =44.5)
- Calculate the mode
- Draw the cumulative frequency curve then estimate the median
12. (a)Four positive numbers are consecutive elements of geometric progression (G.P).The product of the first and the third number is 36 while the product of the second and fourth number is 324. Find the sum of nine terms of the G.P
(b) The second , fourth and eighth terms of an Arithmetic Progression form a Geometric progression and the sum of the third and fifth terms of AP is 20. Find the first four terms of the geometric progression.
13. (a) A function is defined as f(x ) = √4 - 2 find (i) Domain and Range of f(x) (b) Sketch the graph of function f(x)= { + 3 ? < 1
2 ? > 1
Hence (i) state its domain and range (ii) Find f(6) , f(-2) (iii) State whether the graph is one to one function ?
14. The relation is defined as R={(, ): ≥ —4, 3 - 4 ≤ 12 5 + 4 ≤ 20}
- Draw the graph of R
- State the domain and range of R
FORM THREE MATHEMATICS EXAM SERIES 64
FORM THREE MATHEMATICS EXAM SERIES 64
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
FORM III BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 3 Hours Year: 2021
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions.
2.Answer all questions in sections A and B.
3.Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
5.NECTA mathematical tables and non-programmable calculator may be used.
6. All communication devices and any unauthorized materials are not allowed in the examination room.
SECTION A (60 MARKS)
1.(a) Express the numbers 1470 and 7056 each as a product of its prime factors.
Hence evaluate and simplify
![]()
if m = 1470 and n = 7056.
(b)Express 0.00152 correct to: (i) two (2) significant figures
(ii)three (3) decimal places
(iii)in standard form
2.(a) Express x and y into fraction and hence find x + y, given that
![]() and
and ![]()
(b)Solve for x in the following equation
![]()
3.(a) Solve for n
![]()
(b) Given that x2 + 8x +Q = (x + K)2
4 .In a certain school, 40 students were asked about whether they like tennis or football or both. It was found that the number of students who like both tennis and football was three times the number of students who like tennis only. Furthermore, the number of students who like football only was 6 more than twice the number of students who like tennis only. However, 4 students like neither tennis nor football.
(a)Represent this information in a Venn diagram, letting x be the number of students who like tennis only.
(b)Use the results obtained in part (a) to determine number of students who likes;
(i)Football only.
(ii)Both football and tennis.
5.(a) Find the equation of the line through the point (2,?2) crossing the ![]() -axis at the same point as the line whose equation is y=2x- 4
-axis at the same point as the line whose equation is y=2x- 4
(b) Express y in terms of x; 3x + 2y = 6 and Without drawing the graph, state the gradient, the y – intercept and x – intercept in the equation.
6.(a) The length of a rectangular field is 20m longer than the width. Find an expression for the perimeter of the field in terms of its length.
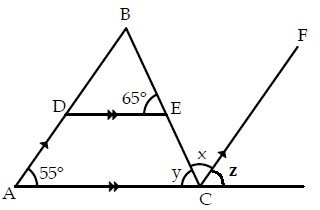
(b) In the figure below, Find angle x, y and z
7.(a) The parallel sides of a trapezium are 8cm and 12cm respectively. If the distance between the parallel sides is 9cm, calculate its area.
(b) A lady buys a printer for sh.26000 and when she sells it she realizes a loss of 40%. How much did she sell the printer for?
8. (a) If y2 varies directly as x-1 and inversely as x+d and if x=2, d=4 for y=1, then find x when y=2 and d=1.
(b)If 8 students in a typing pool can type 210 pages in 3 days, how many students will be needed to type 700 pages in 2 days?
9.(a) If ![]()
Find
i) Cos A
(ii)
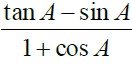
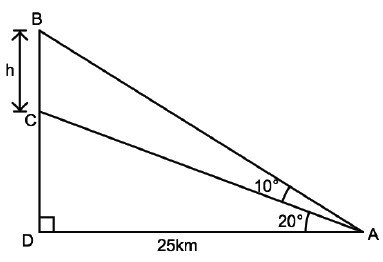
(b) Given the following figure, find the value of h, correct to one decimal place
10.(a)Compute the sum of the first ten terms of the series 1+5+9+....
(b)The 5th term of A.P is 23 and the 12th term is 37. Find
(i)The eleventh term
(ii)The sum of the first eleventh terms by using the values computed above without using the common difference for this progression.
SECTION B(40%)
Answer All Questions In This Section
11.Given the relation;
![]()
(i)Sketch the graph of R.
(ii)State its domain and range.
(iii)Find inverse of relation R
12. Given that
![]()
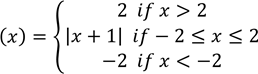
(a) (i) Sketch the graph of f(x)
(ii) State its domain and range (iii) Is f(x) a one - to – one function?
(b) Find:
( i ) f(-4)
( ii ) f(2)
( iii ) ![]()
![]()
![]()
![]()
13. The masses of 40 parcels handled at transport office were recorded as shown in table below
| Mass(kg) | 1.0- 1.9 | 2.0-2.9 | 3.0-3.9 | 4.0 - 4.9 | 5.0 - 5.9 | 6.0 - 6.9 |
| Number Of Parcels | 6 | 2x | 10 | x | 2 | 1 |
a)Find value of x
b)Determine modal class and its corresponding class mark
c)Find Median
14.( a) Given f(x) = x2 - 4x + 2. Find
i) Axis of symmetry ii) Maximum or minimum value
iii) Turning point
(b)Draw the graph of f(x) in 14(a) and use it to solve the equation x2 - 4x -2 =3
FORM THREE MATHEMATICS EXAM SERIES 56
FORM THREE MATHEMATICS EXAM SERIES 56
PRESIDENT'S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
Time: 3 Hours November 2020 a.m.
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions.
2.Answer all questions in sections A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
3.All necessary working and answers for each question must be shown clearly.
4.mathematical tables may be used.
5.Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
SECTION A (60 Marks)
Answer all questions in this section.
1.a) Use mathematical table, evaluate
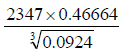
(b)Express 5.4545454545... in form of a/b where a and b are both integers.
2.(a)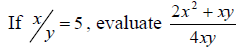
b)Solve for x the following equation 32x-3 X 8x+4 = 64 ÷ 2x
c)Rationalize the denominator
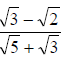
3.a) Find value of P which makes the following equations perfect square
i) x2 + 8x +P=0
ii) x2 - ![]() x + P=0
x + P=0
b) Solve for x the equation
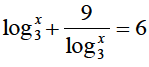
4.a)Given the universal set U={p, q, r, s, t, x, y,z} A={p, q, r, t} B={r, s, t, y }.
Find i)(AUB) ii)(A’nB’)
b)In a class of 60 students, 22 students study Physics only, 25 study Biology only and 5 students study neither Physics nor Biology. Find i) Number of students study Physics and Biology. ii) Number of students that study Biology.
5.a) A, B and C are to share T.sh 120,000/= in the ratio of![]() :
:![]() :
: ![]() . How much will each get?
. How much will each get?
b)A radio is sold at T. sh 40,500/= this price is 20% value added tax(V.A.T). Calculate the amount of V.A.T.
6.(a) Triangles ABC and STBare similar. AB=3cm and ST=2cm. The area of triangle STU is 6cm2. Find the area of triangle ABC
(b) The translation T maps the origin onto a point P(4,8). Where will T map the points: (i) Q(0,4)?
(ii) N(−10,8)
7. (a) Find the equation of the line through the point (2,−2) crossing the ![]() -axis at the same point as the line whose equation is y= x−4
-axis at the same point as the line whose equation is y= x−4
(b) A farmer sold a quarter of his maize harvest and give one third of the remaining to his relatives.If the farmer remained with 36 bags of maize, find:- (i) How many bags of maize did the farmer harvest. (ii) How many bags of maize did the farmer sold.
8.(a) The sum of 1st n-terms of certain series is 2n-1, show that this series is Geometric Progression. Find an the nth term of this series.
(b) )The 5th term of A.P is 23 and the 12th term is 37. Find
(i)The tenth term
(ii)The sum of the first tenth terms by using the values computed above without using the common difference for this progression
9.(a) Given that
Find The value of
![]()
(b) A man standing on top of cliff 100m high, is in line with two buoys whose angles of depression are 170 and 210. Calculate the distance between the buoys.
10. a)Solve for x if
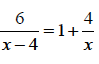
(b) A two-digit of positive number is such that, the product of the digits is 8. When 18 is added to the number, then the digits are reversed. Find the number.
SECTION B (40 MARKS)
Answer All Questions In This Section
11. The daily wages of one hundred men are distributed as shown below
| Wages in T.Sh. x 1,000 | 3.0 - 3.4 | 3.5 - 3.9 | 4.0 - 4.4 | 4.5 - 4.9 | 5.0 - 5.4 | 5.5 - 5.9 | 6.0 - 6.4 | 6.5 - 6.9 |
| Number of men | 4 | 6 | 10 | 14 | x | 20 | 14 | 6 |
a)Find the value of x
b)Calculate the daily mean wage of the 100 men
c)Draw histogram to represent this data and use it to estimate Mode
d)Draw cumulative frequency curve and use it to represent Median
12.(a ) Find values of angles marked x0 and y0 in the figure below
(b)Prove that exterior angle of cyclic quadrilateral is equal to interior opposite angle.
(c)Two places P and Q both on the parallel of latitude 260N differ in longitude by 400. Find the distance between them along their parallel of latitude
13. .(a)Prepare Balance sheet of Mr. Hamis from the following Assets and Liabilities on 31 st December 2009:
•Creditors 100,000/=
•Debtors 150,000/=
•Bank Overdraft 50,000/=
•Cash in hand 15,000/=
•Stock 85,000/=
•Furniture 42,000/=
•Premises 250,000/=
•Capital 392,000/=
(b) Use the transactions above to find
i.Total current asset
ii.Total Current liability
iii.Working Capital iv. Total fixed Asset
14. a) The function f is defined as follows:
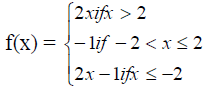
i) Sketch the graph of f(x)
(ii) Determine domain and range (
(iii) Find f(1) , f(-4) and f(π)
(b)For what values of x is function f(x)=![]() is undefined?
is undefined?
FORM THREE MATHEMATICS EXAM SERIES 39
FORM THREE MATHEMATICS EXAM SERIES 39
THE PRESIDENT'S OFFICE
MINISTRY OF REGIONAL GOVERNMENT AND LOCAL GOVERNMENT
AUGUST-SEPTEMBER EXAMINATION SERIES
MATHS FORM-3
2020
TIME: 2:30 HRS
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in sections A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a) If 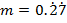 and
and 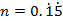 find the fraction of
find the fraction of ![]() in its simplest form
in its simplest form
(b).Find the GCF of 210, 357 and 252.
2.(a)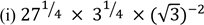
(ii) log3 10 + log3 8.1
(b) If nlog5125 = log264 , find the value of n.
3. (a) By substituting a = 1x and b = 1y in the system of equations:
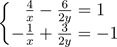 , find the solution set (x,y).
, find the solution set (x,y).
(b) Let U be a universal set and A and B be the subsets of U where:
U = {1,2,3,4,5,6,7,8,9,10}, A = {odd numbers} and B = {prime numbers} (i) Represent this information in a venn diagram.
(ii) Find A ? B′ and (A ? B) ′
4. (a) Given vectors (i) the vector a = 3i + 2 j , b = 8i + 3j and c = 2i + 4 j find:
(i) d=3a -b +1/2c
(ii) a unit vector in the direction of d.
(b) Find the equation of the line passing at point (6, 2) and it is perpendicular to the line that crosses the x-axis at 3 and the y-axis at 4.
5. (a) Two triangles are similar. A side of one triangle is 10 cm long while the length of the corresponding side of the other triangle is 18 cm. If the given sides are the bases of the triangles and the area of the smaller triangle is 40 cm2 , find the area and the height of the larger triangle.
(b) In the figure below CB = BD = DA and angle ACD = x .
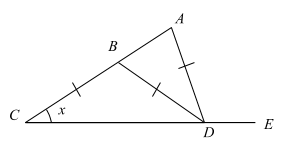
(i) Show that angle ADE = 3x ,
(ii) Calculate the measure of angle CDA if x = 39°.
6. (a) A shopkeeper makes a 20% profit by selling a radio for sh. 480,000.
(i) Find the ratio of the buying price to the selling price.
(ii) If the radio would be sold at 360,000, what would be the percentage loss?
(b) A farmer sold a quarter of his maize harvest and gave one third of the remaining to his relatives. If the farmer remained with 25 bags of maize find how many bags of maize did the farmer harvest.
7. (a) Mariam, Selina and Moses contributed 800,000, 1,200,000 and 850,000 shillings respectively while starting their business.
(i) Find the ratio of their contributions in simplest form.
(ii) If the business made a profit of 1,900,000 shillings; find how much each got if the profit was shared in the same ratio as their contributions.
(b) A dealer bought 10 books for 200,000. He sold 25 of them at 30,000 shillings each and the remaining at 25,000 shillings each. What was his percentage profit?
8. (a) The number of tablets given to a patient was found to be directly proportional to the weight of the patient. If a patient with 36 kg was given 9 tablets, find how many tablets would be given to a patient whose weight is 48 kg.
(b) Four people can eat 2 bags of rice each weighing 10 kg in 12 days. How many people can eat 6 bags of rice of the same weight in 18 days?
9. (a) If the sum of n terms of a geometric progression with first term 1 and common ratio ![]() is
is ![]() , find the number of terms.
, find the number of terms.
(b) How many integers are there between 14 and 1,000 which are divisible by 17?
10.(a) Use factorization method to solve the quadratic equation x2 ? 9x + 14 = 0.
(b) Find the values of x that satisfies the equation
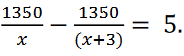
SECTION B( 40 Marks)
Answer All Questions
11.(a) A ship sails from Pemba (4.5°S, 39.5°E) to Dar es salaam (7.5°S, 39.5°E). If it leaves Pemba at 11:30 am and arrived in Dar es salaam at 13:30 pm, use  and RE=6370km to find speed of ship in km/h
and RE=6370km to find speed of ship in km/h
11.(b) Calculate the values of 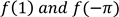 if f is defined as
if f is defined as
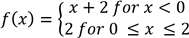
12.Mwanne commenced business on 1st April, 2015 with capital in cash 200,000/=
April 2 bought goods for cash 100,000/=
3 bought goods for cash 300,000/=
4 purchased shelves for cash 230,000/=
5 sold goods for cash 400,000/=
9 paid wages for cash 50,000/=
12 purchased goods for cash 70,000/=
13 sold goods for cash 600,000/=
16 paid rent for cash 100,000/=
20 bought goods for cash 60,000/=
25 sold goods for cash 300,000/=
27 paid salary for cash 70,000/=
Prepare the following:
(a) Cash account, (b) Trial balance.
13. The heights of 50 plants recorded by a certain researcher are given below:
56 82 70 69 72 37 28 96 52 88 41 42 50 40 51 56 48 79 29 30 66 90
99 49 77 66 61 64 97 84 72 43 73 76
76 22 46 49 48 53 98 45 87 88 27 48
54 79 80 73
(a) Copy and complete this tally table for the data given above.
| Height (cm) | Tally | Frequency |
| 21-30 | ||
| 31-40 | ||
| 41-50 | ||
| 51-60 | ||
| 61-70 | ||
| 71-80 | ||
| 81-90 | ||
| 91-100 |
Use this table to:
(b) Draw a histogram for the height of the plants.
(c) Find the mean height of the plants (do not use the assumed mean method).
(d) Find the median of the heights of the plants.
14. (a) In the figure below, BD is a tangent to the circle having the centre O .
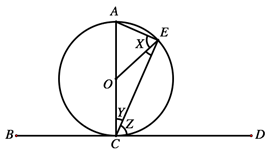
Given that angle OEC = 28°, find the values of angles marked X , Y and Z .
(b) Find the equation of the line passing at point (6, 2) and it is perpendicular to the line that crosses the x-axis at 3 and the y-axis at 4.
FORM THREE MATHEMATICS EXAM SERIES 29
FORM THREE MATHEMATICS EXAM SERIES 29
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
BASIC MATHEMATICS TERMINAL EXAMINATION-MAY
FORM THREE
Time 3:00 Hours MAY 2020
Instructions
- This paper consists of two sections A and B.
- Answer all questions in Section A and only four questions in section B
- Show clearly all working for each question
- Mathematical tables, geometrical instruments and graph paper may be used where necessary
SECTION A (60 MARKS)
1. (a) Arrange the number ![]() in ascending order.
in ascending order.
(b) Express 0.06896 correct to:
(i) three (3) significant figures
(ii) three (3) decimal places
(iii) in standard form
2. (a) Solve for x in the equation: 32x-3 x 8x+4 = 64 ÷ 2x
(b) Solve for x in the equation log(x2+8) – logx = log6
3. (a) Find the solution set of the inequality ![]() and indicate it on a number line.
and indicate it on a number line.
(b) If ![]() find n if
find n if ![]()
(c) Simplify the following expression and state the coefficient of ![]()
![]()
4. (a) In a school of 75 pupils, 42% of the pupils take Biology but not Chemistry, 32% take both subject and 10% of them take Chemistry but not Biology. How many pupils do not take either Biology or Chemistry?
( b) The Venn diagram below shows the universal set U and its two subsets A and B
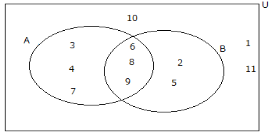 Write down the elements of
Write down the elements of
i) A’ ii)B’ iii)AUB iv) A’UB’
5. The figure ABCD below is rectangle with sides as shown where C1 and C2 are two quarter circles inside it.
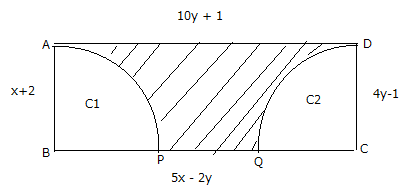
Find:
a) Value x and y shown in the figure above
b) Perimeter of the rectangle
c)Area of the rectangle ABCD
d) Area of the shaded region
6. (a) The variable v varies directly as the square of x and inversely as y. Find v when x = 5 and y = 2; given that when v = 18 and x = 3 the value of y = 4.
(b) The temperature (Ti) inside a house is directly proportional to the temperature (to) outside the house and is inversely proportional to the thickness (t) of the house wall. If
Ti = 320C when To =240C and t = 9 cm, find the value of t when Ti = 360C and To = 180C
7. (a) A shirt whose marked price is Tshs 80,000/= is sold at a 13% discount, if the trader makes a profit of 20%, find the selling price of the shirt.
(b) A regular polygon has an exterior angle of 360
- Find the size of the interior angle
- How many sides does this polygon have
- Find the sum of interior angles of this polygon
8. (a) Find the 10th term of the G.P if the 4th term is 8 and the 7th term of this G.P is 16.
(b) Find the sum of the first 10 terms of the series: 4 + 6 + 8 + - - - - - - - -
9. (a)Find the value of ![]() without using mathematical tables.
without using mathematical tables.
(b) A ladder leans against vertical wall. If the ladder reaches 12m up the wall and its foot is 9 cm from the base of the wall. Find the length of the ladder.
10. (a) Factorize completely ![]() by splitting the middle term
by splitting the middle term
(b) Factorize ![]() and hence find exact value of (10003)2 –(997)2
and hence find exact value of (10003)2 –(997)2
(c) Solve the equation ![]()
SECTION B ( 40 MARKS )
(a) The function f is defined as follows:
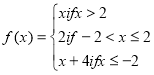
(i) Sketch the graph of ![]() .
.
(ii) Determine the domain and range of ![]()
(b) If R-1 =![]() . Find the domain and range of R
. Find the domain and range of R
12. The 4th, 6th and 9th terms of arithmetic progression forms first three terms of geometric progression. If the first term of the A.P is 3, determine the:
(a) Common difference of the arithmetic progression
(b)Common ratio of the geometric progression
(c) Kicheche deposited Tshs100000/= in a bank at a compound interest of 8% per annum for 4 years. Find how much interest he received
13. The weight in kg of 40 students were recorded as follows:
| Weight in(kg) | 10 - 19 | 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | 60 - 69 | 70 - 79 |
| Number of students | 8 | 3 | x | 8 | 7 | 2 | 2 |
Calculate:
(a) The value of x
(b) The mode by using the formula.
(c) By using an assumed mean, find the average weight of the students
(d) Draw a cumulative frequency curve and hence use it to estimate median.
14. a) A farmer sold a quarter of his maize harvest and give one third of the remaining to his relatives. If the farmer remained with 36 bags of maize, find:-
i) How many bags of maize did the farmer harvest.
ii) How many bags of maize did the farmer sold.
b)A shopkeeper makes a profit of 20% by selling a TV for 480,000/=
i) Find ratio of buying to selling price
ii) If the radio would be sold for 360,000/=, what would be the percentage loss?
15. The function f is defined as follows:
f(x) = 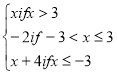
![]()
i) Sketch the graph of f(x)
ii) Determine domain and range
iii) Find i) f(0) ii) f(-6) iii) f(π)
b)For what values of x is fuction f(x)=![]() is undefined?
is undefined?
16. Mr. Chakubanga started business on 15th February, 2005 with capital in cash 1,055,000/=
February 16 Bought goods for cash 500,000/=
18 Bought shelves for cash 55,000/=
19 Sold goods for cash 450,000/=
20 Purchases for cash 400,000/=
21 Sold goods for cash 700,000/=
25 Paid rent for cash 150,000/=
Required: Record the above transactions in the respective ledgers and extract a trial balance.
FORM THREE MATHEMATICS EXAM SERIES 21
FORM THREE MATHEMATICS EXAM SERIES 21
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
MID TERM EXAMIATIONS
024 MATHS- THREE
Duration: 2:30 Hours
INSTRUCTIONS.
- This paper consists of two sections A and B.
- Answer all questions in section A and only Four Questions in Section B
- All writing must be in blue or black ink except drawing which must be in pencil.
- Calculators, cellular phones and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number at the top right corner of every page.
- Show clearly all working for each question
SECTION A( 60 %)
- a) 468 – 468 ÷39 + 39 correct to two significant figures
b) Calculate without using mathematical tables
![]()
2. Make x subject of the formula
P=![]()
3. By using the substitution t=3x, solve the equation 32(1+x) – 3x=3(x+3)-3
4. The size of exterior angle of a regular polygon is 450. Find :
i) The number of sides
ii) The sum of all interior angles
5. Find the values of x that satisfy the following equation log(x+5) + log(x + 2)=log4
6. A translation T carries the point (1,2) to (-2,8). Find where it map :
a) Pont A(-2,2)
b) The origin
7. The lines with equations 2x=3 – y and 2y + 3x=4 meet at point Q. Find the coordinate of point Q.
8. Find two consecutive odd numbers whose product is 195.
9. In a class of 31 students, 17 participate in English debate, 12 participate in English and Sports. If every student is required to participate at lest one of the two events. Find the number of students who participate in i) Sport ii) English only.
10. A dealer bought 10 books for 400,000/=. He sold 2/5 of them at 40,000/= shillings each and the remaining at 60,000/= shillings each. What was the percentage profit?
SECTION B(40%)
11. The examination scores in Basic Mathematics of 40 students are given in the following cumulative frequency table.
| Class Interval | 10 - 19 | 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | 60 - 69 |
| Cumulative Frequency | 3 | 6 | 12 | 22 | 35 | 40 |
a) Find the mean using Assumed mean A=44.5
b) Calculate median
c) Draw histogram and use it to estimate Mode
12. a) Consider the figure below where PQ//BC.
i)Prove that triangle ABC is similar with triangle APQ
ii) If the length of BC=15, PQ=9cm and PB= 6cm. Find the length of AP.
b)Prove that, the sum of two angles of a triangle is equal to exterior angle of the third angle.
13. a) Find the expressions which describe the relation of the graph below
b) Determine Domain and range of this relation.
c) Find inverse of this relation.
14 a) Given f(x) = -x2 + 4x – 5. Find
i) Axis of symmetry
ii) Maximum or minimum value
iii) Turning point
b) Draw the graph of f(x) and use it to solve the equation -x2 + 4x -15 =0
15.The function f is defined as follows:
F(x) = 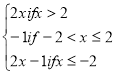
![]()
i) Sketch the graph of f(x)
ii) Determine domain and range
iii) Find
(a) f(1) b) f(-4) c) f(π)
16. Given: Opening Stock 01/01/2012 34,430/=
Closing Stock 31/12/2012 26,720/=
Net purchases during 2012 212,290/=
Expenses for the year 45,880/=
Gross profit is 45% of cost of sold goods.
Find a) Average Stock b) Cost of Sold Goods c) The gross profit d) Net Profit
FORM THREE MATHEMATICS EXAM SERIES 7
FORM THREE MATHEMATICS EXAM SERIES 7
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256