PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
ADVANCED CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
MOCK EXAMINATION SOUTHERN ZONE (MTWARA AND LINDI)
141BASIC APPLIED MATHEMATICS
(For Both School and Private Candidates)
Time: 3 HoursTuesday, 01st February, 2022 a.m.
![]()
Instructions
1.This paper consists of ten (10) questions each carrying ten (10) marks.
2.Answer all questions.
3.All necessary working and answers of each question done must be shown clearly.
4.Mathematical tables and non-programmable calculators may be used.
5.Cellular phones and any unauthorized materials are not allowed in the examination room.
6.Write your Examination Number on every page of your answer booklet(s).

(c)Find the mean and variance of the following data correct to 4 decimal places
| Interval | 4−8 | 9−13 | 14−18 | 19−23 | 24−28 | 29−33 |
| Frequency | 5 | 3 | 1 | 2 | 6 | 4 |
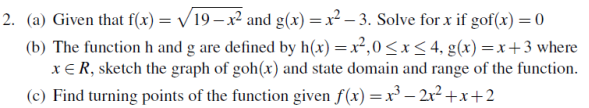
3.(a) The first term of a Geometric progression (G.P) is 1. The sum of the third and fifth terms is 90. Find the common ratio of the G.P.
(b)If the sum of n terms of an AP is 3n2 +5n and its mth term is 164, find the value of m.
(c)Given 4x2 −12x+B find the value of B if that equation has equal roots.
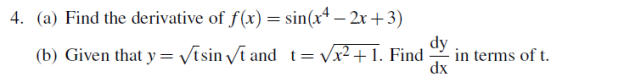
(c)Find the dimensions of a rectangle with perimeter 1000m so that the area of the rectangle is a maximum.
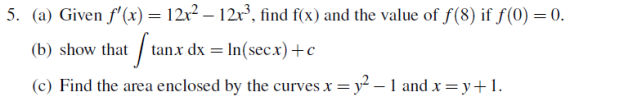
6.Given the following distribution table.
| Class Interval | 7−14 | 15−22 | 23−30 | 31−38 | 39−46 | 47−54 | 55−62 |
| Frequency | 17 | 12 | 24 | 43 | 31 | 14 | 22 |
(i)Construct a cumulative frequency curve, hence estimate the median.
(ii)Calculate the mean by direct mean method
(iii)Calculate the mean by Assumed mean method.
7.(a) A card is drawn at a random from a well shuffled deck of 52 cards. Find the probability that the card is a king or red card.
(b)How many numbers greater than 1000 can be formed with the digits 3,4,6,8,9 if a digit cannot occur more than one in a number?
(c)Given that events A and B are such that P(A)![]() ,P(B)=p and P
,P(B)=p and P![]() , find the value of p if A and B are
, find the value of p if A and B are
(i)Mutual exclusive events
(ii)Independent events
8.(a) Prove that sin3θ=3sinθ−4sin3θ
(b)Given thatx =sinθ then solve 8x3 +1=6x for 0? ≤θ≤360?
(c)The triangle XYZ has an area of 225cm2 of which XY=25cm,YZ=36cm as shown below.
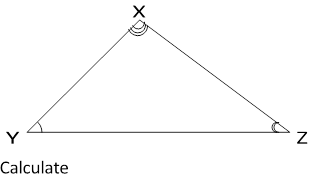
(i)XYˆZ
![]()
(ii)XZ
9.(a) Evaluate![]() dx
dx
(b)What will Tsh.500 account to in 10 years after its deposit in a bank which pays annual interest of 10% compounded annually?
(c)If A.M and G.M of roots of a quadratic equation are 8 and 5 respectively, then obtain the quadratic equation
10.A calculator company produces scientific and graphic calculators. Long term prediction indicates an expected demand of at least 100 scientific calculators and 80 graphic calculators each day. Because of limitations on production capacity, no more than 200 scientific and 170 graphic calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators must be shipped each day. If each scientific calculator sold results in 2000/= loss and each graphic calculator produces 5,000/= profit, how many of each type should be made daily to maximize net profit. What is the maximum profit per day?
FORM SIX BAM EXAM SERIES 7
FORM SIX BAM EXAM SERIES 7
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256