FORM ONE MATHEMATICS EXAM SERIES 226
FORM ONE MATHEMATICS EXAM SERIES 226
FORM ONE MATHEMATICS EXAM SERIES 200
FORM ONE MATHEMATICS EXAM SERIES 200
OFFICE OF THE PRESIDENT, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
MID TERM EXAMINATION
MATHEMATICS FORM ONE
MARCH-APRIL-2025
- (a) Differentiate between rational and irrational numbers.
(b) Convert the fraction below into mixed fraction
(i) 13/5 (ii) 16/3
2. (a) Convert the number below into fraction;
(i) 0.3333..
(ii) 0.4747474…
(b) Convert the following into fraction
(i) 0.3, where 3 is recurring
(ii) 0.83 where 8 and 3 are recurring
3.(a) write any three irrational numbers
(b) Find irrational number such that x2=7
4.(a) What are real numbers
(b) Evaluate
(i) |-2|
(ii) |-3x6|
5.(a) Write each of the following fractions into decimals
(i) 5/9
(ii) 29/6
(b) If x = 1.3 recurring and y=0.21 recurring find value of xy and x-y
6. If a pond has a capacity of 35,000 litres of water, how long does it take to be filled by a hose with capacity of filling 13 litres per minute?
7. There are 64 pipes each with a length of 4.22m arranged horizontally end to end. Estimate the length of all the pipes.
8. A tablet contains 0.1763688 milligrams of a certain chemical. A dose requires a child to take ½ tablet three times a day for 7 days. Find the total amount of chemical in the dose correct to hundredths of a milligram.
9. Show the relationship between mathematics and;
(i) Business studies
(ii) Geography
(iii) History
(iv) Literature
10. Briefly explain importance of studying mathematics
FORM ONE MATHEMATICS EXAM SERIES 198
FORM ONE MATHEMATICS EXAM SERIES 198
PRESIDENT’S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES,
MID TERM ONE – MARCH-2024
MATHEMATICS FORMONE
Time: ..............
Instructions
1. Answer all questions
2. All necessary working and answers for each question must be shown clearly.
3. NECTA Mathematical tables and non-programmable calculator may be used.
- (a) Amani deposited Tsh 360,000 in her bank account. If the bank account charges 100 for every withdrawal. Calculate amount of money remained in her account if :
(i) She withdraws Tsh 106,000.
(ii) She makes a further withdraw of Tsh 50,000 from the remained amount
(b) Re- writes the number 2.430 as mixed fraction
- A dog, a cat and a goat have masses 30.7 kg, 13.44 kg and 18.26kg respectively. Calculate the mass of all three animals giving the answer in nearest whole number.
(b) Round the masses of dog to nearest ones, mass of cat correctly to one decimal place and goat to 3 significant figures
- (a) Asha and Juma received 630,000 shillings from their father. The father wanted to give Asha twice as much as much money as the amount that could be given to Juma. How much did Asha receive?
(b) By using listing method write the lowest common multiple of 3, 10 and 15
- (a)Write the fractions 2/3, 5/3, 5/8 and ½ in order of magnitude starting with smallest fraction, and find product of fraction above.
(b Subtract 0.03 of Tsh 270,000 from 36% as product of prime.
- (a) Write each of the numbers 18, 24, and 36 as product of prime factors and hence find their greatest common factor
(b) Write the numbers 0.009765
- Correct to 3 decimal places
- Correct to three significant figures
- State the place value of 9 in the given number
- (a)Write in numerals: Six hundred thousand and sixty six
(b) In a School there is a menu that has already been prepared for students. In every 5 days mango fruits is provided for lunch, every 4 days fish and every 9 days mixed salad. if today all the three types of food given above are in all today’s menu. After how many days will all three types of food be found together in the menu?
- (a) Change 0.230 into fraction
(ii) Amos scores 27 marks out of 45 scores in mathematics. What percentage is this?
(b) Approximate 13.95 and 9.72 to nearest tens, hence evaluate 13.95*9.72 by using approximated numbers
- The age of the Father is three times the age of his son. If the sum of their ages is 64 years. Find their age.
(b) In a sales promotion, the price of a shirt costing Sh 15000 is reduced by 15%. What is the new price for the shirt?
(a) Find the value for this expression.
![]() -3(
-3(![]() +1
+1![]() -
-![]() )
)
- (b) An article was sold for Tshs 160,000 at the profit of 25%. Find the buying price of the article.
- (a) The sum of two numbers is 127. If the difference between the number is 7. Find the number
(b) Find the value of 0.0000234*120 in standard notation correct to three significant figures
FORM ONE MATHEMATICS EXAM SERIES 166
FORM ONE MATHEMATICS EXAM SERIES 166
PRESIDENT OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSESSMENT
BASIC MATHEMATICS FORM ONE
ANNUAL EXAMINATION 2023
Instructions
- This paper consists of ten (10) compulsory questions.
- Show clearly all the working and answers in the space provided.
- All writing must be in blue or black ink except drawing which must be in pencil.
1.(a) (i) Add the first three multiples of 2, 3 and 5.
(ii) The numbers K, 2, 3 and 5 have an average of 5. What is the number represented by the letter K?
(b) Re-write the number ![]() as a mixed fraction.
as a mixed fraction.
2. (a) The number of pupils in three primary schools is as follows. Iganzo primary school is 1600 pupils, Ruanda primary school is 1500 pupils and Ilea primary school is 1800 pupils. Approximate the number of pupils of the three schools to the nearest thousands.
(b) Calculate (80kg 49g) – (39kg 850g)
3.(a) (i)Arrange 2/5, 5/8 ,48% and 0.6 in ascending order
(ii) Show on the number line the solution set of the inequality
?2x+1?>3
(b) Equal squares as large as possible are drawn on a rectangular board measuring 54cm by 78cm. Find the largest size of the squares.
4.(a) Solve 3 - ![]() of (6x+9) = 5-2x
of (6x+9) = 5-2x
(b) Solve the following simultaneous equations
2x+3y=5
4x+23=5y
5(a) One - third of the sum of ages of Ana and Asha is 50 years, and one - fifth of the difference of their ages is 2 years, find the age of Ana and Asha respectively.
(b) The width of the football ground is 40m. If the area of the same football ground is 1700m2
(i) find the length of the football ground
(ii) if the person has to walk around the football ground, what length of the football ground is expected to be covered by the person?
6.(a) Differentiate between rational number and irrational number
(b) Sketch the graph of the equation x-2y=4
7. (a) A car was sold at a profit of 90000 shillings. If the rate of profit is ![]() % , find the purchasing price of the car and its selling price?
% , find the purchasing price of the car and its selling price?
(b) Mr. Juma deposited a certain amount of money in a bank for a period of 3 years at the rate of 3.5% which gives an interest of 8400 shillings. Determine the amount of money that Mr. Juma deposited initially.
8.(a) (i) John, Ramadhani , Marry and Sam have 600 ,100, 500 and 300 shares in a cooperative shop respectively. Divide 150,000 shs among them in the ratio of their shares.
(ii) A real estate agent received a 6% discount on the selling price of a house . If the discount was Tsh.888,000. What was the selling price of the house ?
(b) Find the area of the shaded region in the figure below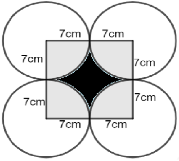
9. (a) Study carefully the figure below
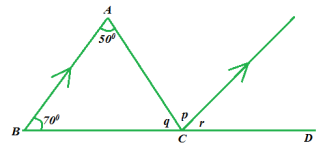
- Find the values of the angles marked p, q and r respectively.
- Find the value of p+q+r
(b) If 2x +700 and 3x+200 are supplementary angles, determine the value of x
10.(a) If the straight line CD which is passing through the points C (2 , 6) and D ( K , 3 ) has a gradient of -1, find the value of K.
(b) Find equation of a line passing through point ( 0 , 3 ) and ( 1 , 2 )
FORM ONE MATHEMATICS EXAM SERIES 157
FORM ONE MATHEMATICS EXAM SERIES 157
PRESIDENT OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSESSMENT
BASIC MATHEMATICS FORM ONE
ANNUAL EXAMINATION 2023
Instructions
Answer all questions from this paper
1. (a) Nine best friends share 52 sweets equally. How many sweets does each friend get and how many remain
(b)A farmer uses ![]() of his farm for giving bananas
of his farm for giving bananas ![]() pineapple
pineapple ![]() for mangoes and remaining portion of his land in used for growing oranges. What fraction of his land used to grow orange?
for mangoes and remaining portion of his land in used for growing oranges. What fraction of his land used to grow orange?
2. (a)A lorry is filed with 7.1 tones of land. During the Journey 210kg of sand either falls or blows away. What mass of sand in tones in delivered at end of Journey?
(b)Juma measured the height of his friend Moses by using a tape measure. He found that his friend was 167.5cm high. Approximate his height
- To 1 significant figure
- To nearest ten
3. (a)The perimeter of a square plot is 240m. What length is its side?
(b)A goat is tied on a post by a rope of length 7m
- Draw the shape of a figure the goat can describe on the land when it is grazing
- What is the area of land the goat can reach?
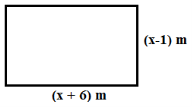
4. (a)The length and width of a rectangular field shown below are respectively (x + 6) metres and (x – 1) metres. Let P be the Perimeter of the field. Write the algebraic expression of P in terms of x
(b)A wooden table is bought for Tsh 80,000 and then sold for Tsh 96,000/=. Find
- The profit made
- Percentage profit
5. (a)If x= 0.2![]() and Y = 5
and Y = 5![]() express X and Y in form of
express X and Y in form of ![]() where
where ![]() and ‘a’ and ‘b’ are integers find value of find value of
and ‘a’ and ‘b’ are integers find value of find value of ![]()
(b)Mr. John has three classes. Each class has 28, 42 and 56 students respectively. Mr. John wants to divide each class into groups so that every group in every class has same number of students and there are no students left. What is the maximum number of students Mr. John can put in each group?
6. (a) Rectangular table top is 2m long. If the area of the rectangular table top is 3.96°m2. Find its width
(b)Solve simultaneous equation below
![]()
7. (a) If Fatuma is 4years less than Bakari and 3times Fatuma’s age is equal to 2 times Bakaris age what are their ages?
(b) Solve ![]()
8. (a) John, Ramadhani, Mary and Sam have 60°, 100, 500, and 300 shares in a cooperative shop respectively. Divide 150,000 shs among them in ratio of their shares.
(b)A real estate agent received a 6% discount on selling price of a house. If the discount was Tsh 888,000. What was selling price of the house?
9 (a) Find the sum of 85% of 9861 and ![]() of 12458. Write your answer in two significant figures.
of 12458. Write your answer in two significant figures.
(b)Jenk and Jerry are riding on a circular path. Jenk complete a round in 24 minutes where as Jerry Complete a round is 36 minutes. If they started at the same place and time and go in same direction, after cows many minutes will they meet again at starting point?
10. (a)If the lines whose equation is y=3x – p passes through points (6,10) and (q, 22) Find the values of P and q, where P and q are integers
(b)Asha and Juma received 630,000 shillings from their father. The father wanted to give Asha twice as much as the amount that could be given to Juma. How much did Asha receive?
FORM ONE MATHEMATICS EXAM SERIES 154
FORM ONE MATHEMATICS EXAM SERIES 154
PRESIDENT OFFICE REGIONAL ADMINISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSESSMENT
MATHEMATICS FORM ONE
MID-TERM EXAMS-AUG – 2023
Instructions
Answer all questions from this paper
- (a) Write 624.3278 correct to
- Five significant figure
- There denial placer
(b)(i)A rope of 18m and 80 cm is to be divided into four equal part. How long will each part be? Give your answer in meters and centimeters.
(ii) 50% of the content in a box weigh 8kg 40gm. What does the whole content weigh?
- (a)A rectangular table top is 2m long. If the area of the rectangular table top is 3.96m2. Find its length
(b)(i)Solve the following simultaneous equation
![]()
(ii)If fatuma is 4 years less than Bakari and 3 times Fatuma’s age is equal to 2 times Bakaris age, what are their ages?
- (a)Three bells ring at intervals of 20 minutes, 30 minutes and 40 minutes. If they start ringing together at 7:30am
- After how long will they ring together again
- At what time will this be?
(b)Round off 349.678 to nearest
(i)Tens (ii) Hundredth (iii) One significant figure
- (a)Perform operation
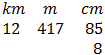
(b)Find the time in which sh 200,000/= will eam sh 48,000 at the rate of 4% interest per annum.
- (a)(i)Write the fraction
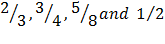 in order of magnitude starting with the smallest fraction
in order of magnitude starting with the smallest fraction
(ii)Find the product of fraction given in part (a)(i)
(b)Subtract ![]() of Tsh 270,000 from 36% of Tsh 50,000
of Tsh 270,000 from 36% of Tsh 50,000
- (a)Find the value of the expression
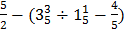
(b)(i)In sales promotion, the price of a shirt costing shs 15,000= is reduced by 15%. What is the new price of the shirt?
(ii)Change ![]() into fraction in its simplest form
into fraction in its simplest form
- (a)Find the value of x and y in the following figure
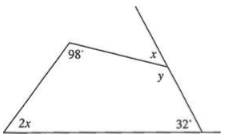
(b)Suppose a metal wire in bend to form a semi-circle with a radius of 14cm. Find (i) The length of the metal wire
(ii)The area bound by metal wire
- (a)Find the creates common factor (GCF) of 18, 24 and 60
(b)The population of three towns are 65, 600, 13,400 and 29,700 to approximate total to the nearest
- (a)Rehema spent
 of her salary on Transport and
of her salary on Transport and  on food. If she remained with shs 80,000, What was her salary?
on food. If she remained with shs 80,000, What was her salary?
(b)Change ![]() into,
into,
(i)Percentage (ii) Decimal
- (a)Lightness, Nancy and zawadi shared some money zawadi got
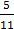 of the money, Nancy got
of the money, Nancy got 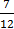 of remaining money. What fraction of the money did lightness get?
of remaining money. What fraction of the money did lightness get?
FORM ONE MATHEMATICS EXAM SERIES 143
FORM ONE MATHEMATICS EXAM SERIES 143
PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM TWO
MID-TERM EXAMS-MARCH – 2023
- (a)Solve
By elimination method
(b)The length of a book exceeds its width by 5cm. Calculate the dimensions of the book given that its area is 50cm2
- (a) A rectangular table top is 2m long. If the area of the rectangular table top is 3.96m2 find its width
(b)(i)Solve the following simultaneous equation
2x + 3y=5
4x + 23 = 5y
(ii) If Fatuma is 4years less than Bakari and 3 times Fatuma’s age equal to 2 times Bakari age. What are their ages?
- (a)(i)x2 + bx + c= (x – 3) + 2) determine the value of b and c
(i) If x2 + ax + 4 = 0 is a perfect square. Find value of a
(iii)Solve the following quadratic equation by completing the square method x2+6x+7 = 0
(b)Solve
- (a)Asha and Juma received 630,000 shilling from their father. The father wanted to give Asha twice an much money as the amount that could be given to Juma. How much did Asha receive
(b)Mr and Mrs. Juma deposited some money in a bank that pays a simple interest of 3% per annum. After 4 years they eamed an interest of 900,000 shillings Determine the amount of money
Determine the amount of money
- Deposited initially
- Accumulated after a period of four years
- (a)if the line equation is y=3x – p passes through points (6, 10) and (9, 22) find the value of P and Q
(b)A mason wants design a small room 500cm. by 200cm.
(i)Draw a diagram of a room at a scale of 1.100
(ii)Calculate the area of the room using the result of 6 (b)(i)
- (a)(i)Write 498,030 in words
(ii)Express the number given in part (a)(i) in standard rotation
(iii)By using listing method, write down lowest common multiple of 3, 10, and 15
(b)(i)Write in numeral; Nine hundred ninety million nine hundred ninety nine thousand, nine hundred and one.
(ii)Determine the number of significant figures in each of numbers, 400, 780 and 0.00606, then approximate each number into one significant figure.
- (a)Find the value of x in the equation
(b) If , Find the value of x
- (a)If
Find value of x and Y
(b)(i) Find value of 0.0000234 x 120 in standard rotation correct is 3 significant figures
(ii)Rationalize the denominator of the expression
- (a) A machine that costs shs 180,000 was sold at a profit of 40%. Find the selling price
(b)A father divided shs 150,000 among Rose and Japheth in the ratio of 2:3 respectively. How much money did each get?
- (a)Find the value of x equation 9 x 34x+ = 27(x – 1)
(b)Factorize the expression 6x4x – 11x + 4 by splitting the middle term.
FORM ONE MATHEMATICS EXAM SERIES 127
FORM ONE MATHEMATICS EXAM SERIES 127
THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL OF TANZANIA
FORM ONE TERMINAL EXAMINATION
BASIC MATHEMATICS
Time: 2:30 Hours Year : 2022
Instructions
1. This paper consists of ten (10) compulsory questions.
2. Show clearly all the working and answers in the space provided.
3. All writing must be in blue or black ink except drawings which must be in pencil.
4. NECTA mathematical tables, geometric instruments and graph papers may be used where necessary.
5. All communication devices, calculators and any unauthorized materials are not allowed in the assessment room.
1(a) Subtract 25% of 24 from 6
(b)On a number line perform an operation of -4 – 3
2(a)Find the sum of ![]()
(b)If 0.000701 is expressed in the form A x 10n, where 1≤A<10 and n is an integer, find the value of n
3. Re-arrange the order of the digits in the number 5879613 to make it
- The largest number
- The smallest number
4.Convert (a) 4 kilometers + 8 hectometers into centimeters
(b)24 hours into seconds
5.(a)Arrange the following numbers from the largest to the smallest ![]()
(b)Given the number 0.00803, write the number of significant figures.
6.(a)If a*b= (a – b) / (a + b), find 7*3
(b)A clock loses 4 minutes every day. If the clock is set to start on Monday, on which day will it have lost 1 hour?
7.(a)Simplify ![]()
(b) A person borrows Tshs 6,000/= for a period of 6 years at 20% simple interest per annum. Calculate the total amount the person will pay back after 6 years.
8.(a) A straight passes through two A(-3,6) and B(-6,3) Find the equation of this line in the form of y = mx + c.
(a) A shopkeeper makes 40% profit by selling an article for Tshs. 63,000/= What would be his percentage loss if he sold the article for Tshs 40,000/=?
9. (a)Simplify ![]()
(b)Approximate 13.95 and 9.72 to the nearest tens, hence evaluate 13.95 x 9.72 by using the approximated numbers.
(c). The length of rectangle is twice its width. If the perimeter of the rectangle is 18cm, find its area.
10.(a) Solve the equation 0.03x – 0.003 = 0.03
(b)The sum of the ages of David and Juma is 80 years. The difference of their ages is 10 years. Find the age of each of them
(c)Solve the following simultaneous equations.
![]()
FORM ONE MATHEMATICS EXAM SERIES 97
FORM ONE MATHEMATICS EXAM SERIES 97
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM ONE BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 2:30 Hours Year: 2022
Instructions
1.This paper consists of ten (10) compulsory questions.
2.Show clearly all the working and answers in the space provided.
3.All writing must be in blue or black ink except drawings which must be in pencil.
4. NECTA mathematical tables, geometric instruments and graph papers may be used where necessary.
1. (a) Given the numbers 8, 12 and 24. Write in set notation: { }:
i. The factors of each integer
ii. The first 3 lowest multiples of each number
(b)Find the H.C.F and L.C.M of the numbers 8,12 and 24 by prime factorization or by method in (a)
(c)Evaluate:
(i) (-8) – (-16) + (-10)
(ii)![]()
2. (a)Evaluate:
(i) Value of m if ![]()
(ii)![]()
(b)Express: 2hours and 30 minutes as a fraction of ![]() hours
hours
(c)Write down the fraction ![]() in ascending order of magnitude.
in ascending order of magnitude.
3.(a)(i) Express 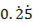 in the form of a/b and find a+b
in the form of a/b and find a+b
(ii)Evaluate: ![]()
(b)Write each fraction as a repeating or terminating decimal
i. ![]() (ii)
(ii)![]()
(c)Express: 17.67547 (i) Correct to 3 decimal place (ii) Correct to 3-significant figures
4. (a) A lorry can take a load of 15 tonnes once. How many times can a pick-up of capacity 3,000kgm take the same amount of 15 tonnes
(b) A plank of wood timber of length 31.5 metres is cut into rectangular pieces of 10.5cm long . How many rectangular pieces can be cut without wasting wood?
(c) Evaluate in terms of hours and minutes
3 x [4hrs + 40 min + 30 sec] and express the result in decimals
5. (a) Factorize
(i) a(c+d) – b(c+d)
(ii) xy + 4x – 2y – 8
(b)Simplify ![]()
(c)Expand (3a + b) (x – y)
6. (a)The diagram represent the frame of a picture (shaded).
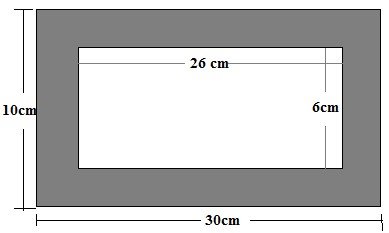
Find the area of the frame
(b)ADEF represent a trapezium
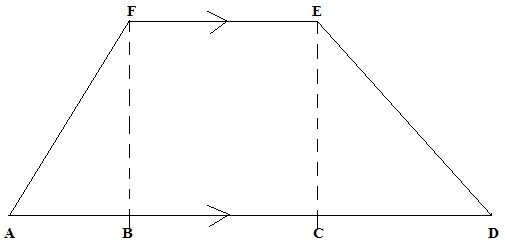
FE=6cm ED=5cm CD=3cm AB=2cm
Calculate the area of the trapezium
7. (a)Given the points A(2,1), and B(8,9)
Find (i) Length of AB
(ii)The slope of AB
(iii)The coordinates of the mid-point M and AB
(b) Find the equation of the line whose slope is ![]() and passing through the point (4,2)
and passing through the point (4,2)
(c)(i)Find the radius of a circle of area 38.5sq.cm, taking ![]()
(ii)How many times does the wheel of a car of radius 10cm. Revolve in travelling a distance of 30![]() metres
metres
8. (a)(i)Solve the following simultaneous equations:
![]()
(ii)Solve for x ![]()
(b)The difference between increasing a number by a number N by 20% and decreasing the same number by 15% is 14. Find N
(c)Solve the following inequalities
(i)![]()
(ii)![]()
9. (a)A 20litre-plastic of cooking oil is bought at 100,000/= and sold at 6,000/= per litre. Find the percentage profit.
(b)Convert the following into percentage
(i)![]()
(ii)![]()
(iii)![]()
(iv)0.03
(c)Convert the following percentages into fractions
(i)20%
(ii)0.8%
(iii)![]()
(iv)3.5%
10. (a)Give one mathematical name for the relation between the following angles and write their relation.
(i)

(ii)

(iii)
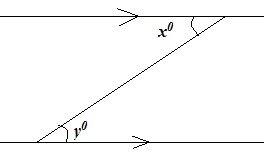
(iv)
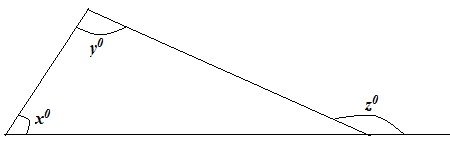
(b)If the angles x°, 2x°, and 3x° are supplementary angles, find the value of x and write down the angles
(c)The angles in a triangle are x°, 2x° and ![]()
Find x and indicate the angles in a triangle
FORM ONE MATHEMATICS EXAM SERIES 96
FORM ONE MATHEMATICS EXAM SERIES 96
![]() PRESIDENT’S OFFICE
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT AUTHORITY
BASIC MATHEMATICS MID TERM-AUG
FORM ONE
TIME: 2:30 HRS
Instructions
Answer all Ten questions
Show all the workings clearly for score awards
Only mathematical tools and writing materials are allowed in the examination room Write your name on each answer script
1. (a) Round 34.796 to the
- Nearest hundredth
- Two decimal places
- Ones
(b) Identify the numbers which are both prime and odd numbers from
15,17,19,21,23,25,27,29,31,33,35, and 37
2. (a) (i) Write 15, 12 and 21 as the product of prime number
(ii) Use the answers in (i) above to deduct the LCM and GCF and the sum of
the LCM and GCF.
(b). Evaluate 3+ (5x(-2+7)) ÷(6+(-3))
3. (a) Compute the difference between the product of -50 and -10 and the sum of -50 and -10 (b) Simplify 3a – 5b - 7a + 6c + 7a + 8b
4. (a) Re – arrange the following fractions in descending order 7 ⁄ 12,3⁄4,5⁄ 6,2 ⁄ 3,1 ⁄2
(b) Express 2.i3? in the form of ⁄ where b≠0 and a and b are integers.
5. (a) Evaluate 28% of the two third of 4,500cm. (b) If m = 2 and n = 2. Compute
(ii) 3(m+2) – 5(n-7)
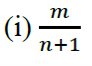
6. (a) A bus leaves the bus station at 06:43am and it takes 2hours and 48 minutes to
reach the destination. What is the arrival time in 24 hours clock system?
![]() (b) Allan set out a travel from Kilalo village to Mandu ward which are 450km apart. He cycled the first 31 of the distance; ran 1 2 of the remaining distance and walked the rest. How many metres did Allan walk?
(b) Allan set out a travel from Kilalo village to Mandu ward which are 450km apart. He cycled the first 31 of the distance; ran 1 2 of the remaining distance and walked the rest. How many metres did Allan walk?
![]()
![]() 7. (a) Gedion was given four number cards with digits 5,2,3 and 9 to formulate the largest and the smallest possible four digits numbers. Write down the numbers that Gedion formed.
7. (a) Gedion was given four number cards with digits 5,2,3 and 9 to formulate the largest and the smallest possible four digits numbers. Write down the numbers that Gedion formed.
(b) Azam biscuit factory packs biscuit in packets of 18, 48 or 60 biscuits each. Identify the smallest number of biscuits that the factory packs in any of these quantities without any biscuit being left over.
8. (a) The sum of two consecutive whole numbers is 109 what are the two numbers? (b) Round off
- 9.67 to ones
- 0.205 to one decimal place
- 0.0197 to two decimal places
Hence use the results to estimate the value of 9.67 0.205
0.0197
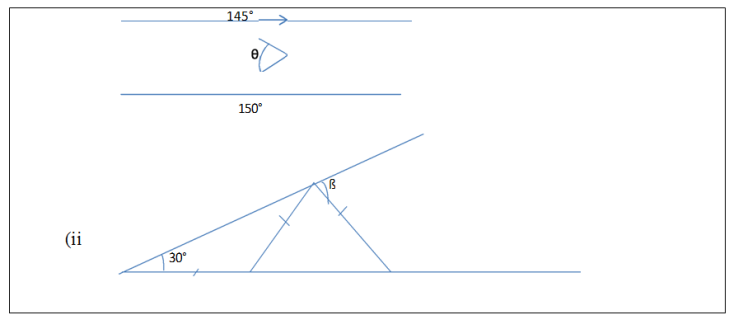
9. (a) Compute the value of the unknowns from the diagrams below
![]() (b) In constructing angles, Amani realized 160° is an interior angle of a regular polygon. He further realized that the regular polygon have n sides and m total internal degrees for the interior angles. Evaluate n and m values.
(b) In constructing angles, Amani realized 160° is an interior angle of a regular polygon. He further realized that the regular polygon have n sides and m total internal degrees for the interior angles. Evaluate n and m values.
10. (a) In Namabengo village 70 percent of 1200 cows are black and 22.3 percent of 18000 donkeys are white. Determine the sum of black cows white donkeys.
(b) How many hours, minutes and seconds are there in 5,480 seconds?
All the best
FORM ONE MATHEMATICS EXAM SERIES 69
FORM ONE MATHEMATICS EXAM SERIES 69
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM ONE BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 2:30 Hours Year: 2021
Instructions
1.This paper consists of ten (10) compulsory questions.
2.Show clearly all the working and answers in the space provided.
3.All writing must be in blue or black ink except drawings which must be in pencil.
4.NECTA mathematical tables, geometric instruments and graph papers may be used where necessary.
5.All communication devices and calculators are not allowed in the assessment room.
1. (a) Write the numerals of the statement: Ninety two million two hundred seventy five thousand two hundred seventy five.
(b) Write the number 2373695 in words.
2. (a) Find the value of 98 – {(15 ÷ 3) – (45 ÷ 15)} × 10 + 4
(b) Simplify the algebraic express and state the coefficient of x: -2( x – 3 ) + 4( -2x + 8)
3.(a) Round off the number 0.007326 correct to:
(i) 3 significant figures
(ii) 3 decimal places
(b) Change the following :
(i) 1608 hrs into 12 – hours clock system
(ii) 7:08 pm into 24 – hours clock system
(iii) 980 dam into centimeters
4.(a) Find the H.C.F of 112, 168 and 420 by prime factorization
(b) The sum of three consecutive odd numbers is 51. Find the numbers.
5. (a) Add the difference of ![]() and
and ![]() to the sum of
to the sum of ![]() and
and ![]() .
.
(b) Express ![]() in form of
in form of ![]() where b ? 0
where b ? 0
6. (a) Solve for x given that ![]()
(b) In a School, ![]() of the students are boys and the number of girls is 990. Find the number of boys in the School.
of the students are boys and the number of girls is 990. Find the number of boys in the School.
7.(a) Three traffic lights at three different road crossings change after 48 seconds, 72 seconds and 100 seconds respectively. If they all change simultaneously at 8:00 am. At what time will they change again simultaneously?
(b) If 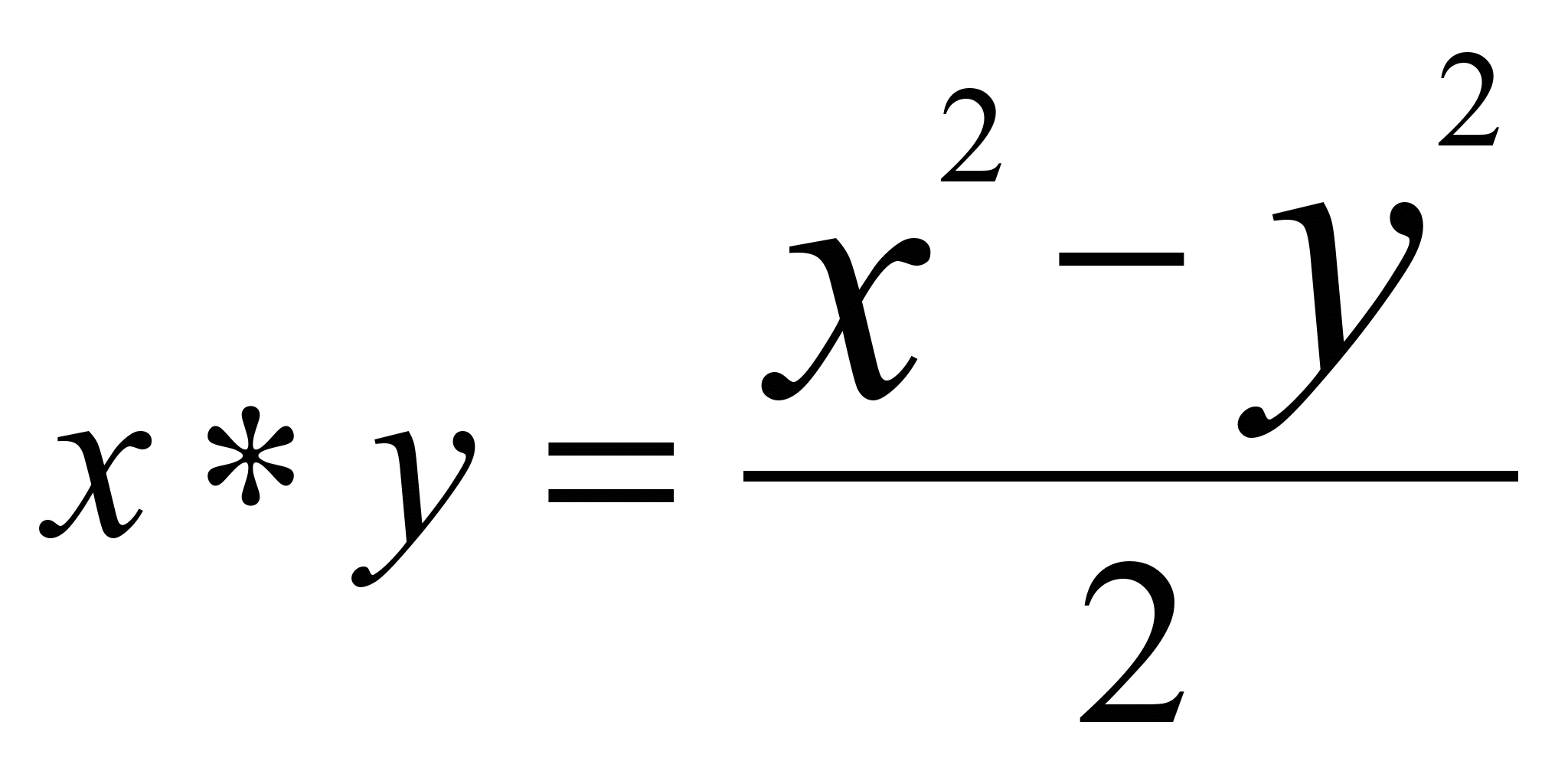 ,find
,find
(i) ![]()
(ii) find n if ![]()
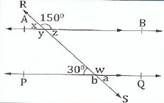
8.(a) In the following figure, AB is parallel to PQ - and RS is a transversal. Find the angles labeled a, b, w, x, y, and z.
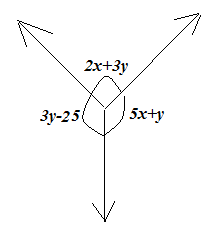
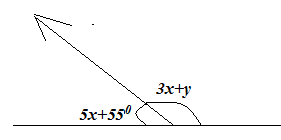
(b) Use the two figures below to find the values of x and y
9. (a )A father is 24 years older than his son. After 2years, the father’s age will be three times that of his son. Find their present ages.
(b) The length of a rectangular park exceeds its width by 17m. If the perimeter of the park is 178m. Find the dimensions of the park.
10. Solve the following simultaneous equations:
(a) 3x – y = 10
5x + 2y = 24 (Using Elimination Method)
(b) 3x + 4y = 17
5x – 2y = 11 (Using substitution method )
FORM ONE MATHEMATICS EXAM SERIES 62
FORM ONE MATHEMATICS EXAM SERIES 62
Student’s Examination No.....................................
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS MID TERM EXAMINATION-MARCH
FORM ONE-2021
TIME: 2.00 HRS
INSTRUCTIONS
- This paper consist of two sections
- Answer all questions
- All work must be shown clearly
- Write your examination number on every page of your answer sheet
- (a) Write 2446 in words
(b) Express 1260 as a product of its prime number
- (a) Write the fraction
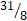 as a mixed number
as a mixed number
(b) How many prime numbers between 40 to 60
- Arrange the following numbers from
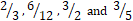
- Ascending order
- Descending order
- Rearrange the order of the digits in the number 5879613 to make;
- Largest possible number
- Smallest possible number
- Which is greater between
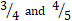
- Use a number line to find;
- Find product of LCM and GCF of 40 and 24
- Perform the following:
- 0.31 + 0.46 – 0.18
- (a) Convert the following into faction
- 1.2.
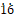
- 0.
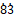
- 0.4

(b) (i) convert ¾ into percentage
(ii) Express 3½% as a decimal
- (a) convert the following into metre
- 3 km
- 939 dm
(b) Find the following;
- Kg g cg
2 8 40
+ 489
________________
.
- Kg g
14 300
+ 8917
__________
1
FORM ONE MATHEMATICS EXAM SERIES 53
FORM ONE MATHEMATICS EXAM SERIES 53
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS MID TERM EXAMINATION
FORM ONE-2021
Time: 2:30Hours
Instructions.
- This paper consists of TEN compulsory questions
- Show all the working and answers in the spaces provided
- All writing must be in blue or blank ink, except drawing which should be in pencil
- Section A carries 35 marks, section B 50 marks and section C 15 Marks
- All answers should be written in the spaces provided.
- All communication devices, calculators and any unauthorized material are not allowed in examination room.
- Write your number on every page of your answer booklet.
FORM ONE MATHEMATICS EXAM SERIES 46
FORM ONE MATHEMATICS EXAM SERIES 46
PRESIDENT'S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
ANNUAL EXAMINATION MATHEMATICS- FORM ONE
Time: 2:30 Hours November 2020 a.m.
Instructions
1.This paper consists of ten (10) compulsory questions.
2.Show clearly all the working and answers in the space provided.
3.All writing must be in blue or black ink except drawings which must be in pencil.
4.Four figure mathematical tables, geometric instruments and graph papers may be used where necessary.
5.All communication devices, calculators and any unauthorized materials are not allowed in the examination room.
1. (a) Write the place value of digits in the brackets
i. 785061 (5) ii. 52401 (2)
(b) Write the following into expanded form
i.720902
ii.53901
2.(a) Write 0.003685 correct to
i) 3-significant figure ii) 3-decimal places
(b) Convert ![]() into decimal, correct to 2-decimal places.
into decimal, correct to 2-decimal places.
3. (a) Change
i) 1608 hrs into 12 – hours clock system ii) 7:08 pm into 24 – hours clock system
(b) The length of 200 dam is what percent of the length of 1.6 km?
4.(a) Find the H.C.F of 112, 168 and 420 by prime factorization.
(b) Three traffic lights at three different road crossings change after 48 seconds, 72 seconds and 100 seconds respectively. If they all change simultaneously at 8:00 am. At what time will they change again simultaneously?
5. (a) Express 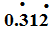 in form of
in form of 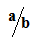 where b ≠ 0
where b ≠ 0
(b) Solve for x given that
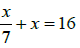
6.(a) Two complementary angles differ by 120. Find the angles
(b) Two angles of polygon are right angles and each of the remaining is 1250. Find number of sides of the polygon and sum of the interior angle.
7.(a) Solve following system of simultaneous equations
![]()
4x - 3y = 22
(b) 10 years ago a man was 12 times as old as his son and 10 years from now a man will be twice as old as his son. Find their present age.
8. (a) What is the absolute value of :
i) 5/6 - 6/7 ii) -3 x 7
(b) Solve the following
![]()
9.(a) A loss of 15% on the price of an item is equal to T.sh 9,000/=. Find the selling price of an item for the profit of 25%.
(b) Find slope, y-intercept and x-intercept of a line 3x + 2y +6=0.
10. (a) In the figure below, find the value of: (i) x (ii) y
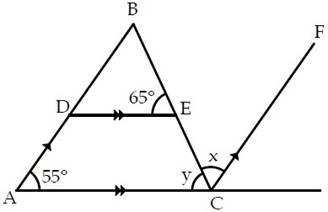
(b) Twice the width of a rectangle is greater than its length by 3cm. If the perimeter of the rectangle is 36cm, find its dimensions
FORM ONE MATHEMATICS EXAM SERIES 34
FORM ONE MATHEMATICS EXAM SERIES 34
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
COMMERCE- TERMINAL EXAMINATION-MAY
FORM ONE
TIME: 2HRS 2020
NAME:_______________________________________________ CLASS:___________
INSTRUCTIONS
- This paper consist of section A,B and C with a total of seven(7) questions.
- Answer all questions.
SECTION A (30 MARKS)
Answer all questions in this section
1. For each of the following items (i) – (x), choose the correct answer from among the given alternatives and write its letter besides it.
(i) The production process in which a farmer grows maize for sale is referred to as
- Direct production
- Direct service
- Indirect production
- Indirect services
(ii) The label which shows the price of particular goods in a shop is called.
- Price list
- Price tag
- Invoice
- Branding
(iii) What is the main purpose of commerce?
- To ridge the gap between wholesalers and retailers
- To bridge the gap between producers and the retailers
- To bridge the gap between producers and consumers
- To bridge the gap between retailers and consumers
(iv) Which one among the following is part of aids to trade?
- Commerce
- Direct services
- Trade
- Communication
(v) A person who coordinates all productive resources and bear the business risks is called.
- A business manager
- An entrepreneur
- Entrepreneurship
- Consumers
(vi) The best way in which individuals and organizations use to protect their businesses against risks is:
- Creating bank account through which all business cash are deposited
- Increasing number of employees into the business
- Insuring their employees through insurance companies
- Insuring their businesses through insurance companies
(vii) Examples of free goods are:
- Tanzania Broadcasting, ITV and star TV
- Refrigerator, tractors and tailoring machine
- Roads, public hospitals and public schools
- Rainfall, sunshine and air
(viii) Which of the following presents a disadvantage of barter system?
- Double coincidence of wants
- Divisibility
- Standard of deferred payment
- Indivisibility
(ix) Which of the following is not included in commerce flow chart?
- Insurance
- Warehousing
- Production
- Transportation
(x) Which of the following group presents a broad classification of occupations?
- Trade and production
- Industrial, commerce and tertiary
- Extractive, manufacturing and constructive industries
- Trade, aids to trade and industrial
2. Match items in list A with the responses in list B by writing the letter of the correct response below the number of the corresponding item in the table provided.
| LIST A | LIST B |
|
|
| LIST A | i | ii | iii | iv | v |
| LIST B |
|
|
|
|
|
3. Complete the following sentences by filling in the blanks with the correct term(s)
- Goods and services that are sold within the country are termed as___________________
- The industries dealing with assembling of already manufactured goods into finished goods are called_____________________
- An auxiliary service which involves exchange of information between people or organization is known as ________________
- The last person to receive goods in the channel of distribution is called_______________
- The art of selling goods in small quantities to the final consumer is called_____________
- Human needs which are not necessary for human survival are called_________________
- Human needs which are necessary for human survival are called____________________
- The process of letting the public be aware about your new products is called____________
- Hair dressing is an example of_____________________
- Anything that can be touched, seen is called__________________
SECTION B (30 MARKS)
Answer all questions in this section
4. With examples briefly explain the meaning of the following terms
- Specific factor of production
- Non – specific factor of production
- Aids to trade
- Capital
- Normal goods
5. a)Define the term supply of labour
b) Mention six factors affecting supply of labour
SECTION C (40 MARKS)
Answer all questions in this section
6. Draw the commerce flow chart and label it clearly
7. Carefully study the table below then complete it by filling in the blanks
| Capital | labour | Total product | Average product | Marginal product |
| 1 | 1 | 10 |
|
|
| 1 | 2 | 25 |
|
|
| 1 | 3 | 43 |
|
|
| 1 | 4 | 57 |
|
|
| 1 | 5 | 66 |
|
|
| 1 | 6 | 73 |
|
|
| 1 | 7 | 78 |
|
|
| 1 | 8 | 81 |
|
|
| 1 | 9 | 82 |
|
|
| 1 | 10 | 82 |
|
|
FORM ONE MATHEMATICS EXAM SERIES 12
FORM ONE MATHEMATICS EXAM SERIES 12
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
MATHEMATICS- TERMINAL EXAMINATION-MAY
FORM ONE
Time 2:30 Hours MAY
Instructions
- This paper consists of two sections A and B.
- Answer all questions in all sections
- Show clearly all working for each question
SECTION A :( 60 Marks)
1. Simplify the algebraic express and state the coefficient of x: -2( x – 3 ) + 4( -2x + 8)
2. Find the value of 98 – {(15 ÷ 3) – (45 ÷ 15)} × 10 + 4
3. Round off the number 0.007326 correct to (a) 3 significant figures (b) 3 decimal places
4. Write the numerals of the statement: Ninety two million two hundred seventy five thousand two hundred seventy five.
5. Write the number 2373695 in words.
6. Find the H.C.F of 112, 168 and 420 by prime factorization.
7. Three traffic lights at three different road crossings change after 48 seconds, 72 seconds and 100 seconds respectively. If they all change simultaneously at 8:00 am. At what time will they change again simultaneously?
8. The H.C.F of two numbers is 18 and their L.C.M is 108. If one of the numbers is 54. Find the other number.
9. Add the difference of ![]() and
and ![]() to the sum of
to the sum of ![]() and
and ![]() .
.
10. Express ![]() in form of
in form of ![]() where b ≠ 0
where b ≠ 0
11. Change (a) 1608 hrs into 12 – hours clock system (b) 7:08 pm into 24 – hours clock system
12. Convert 980 dam into centimetres
13. Solve for x given that ![]()
14. In a School, ![]() of the students are boys and the number of girls is 990. Find the number of boys in the School.
of the students are boys and the number of girls is 990. Find the number of boys in the School.
15. Solve for x given that 2(x – 5) + 3(x – 2) = 8 + 7(x – 4)
16. How many kilograms are there in a milligram
17. A sum of money was divided between Mary and Agnes. Mary gets ![]() of the whole money and her share is Tshs. 4050. What is the total amount of money?. What is Ashura’s share?
of the whole money and her share is Tshs. 4050. What is the total amount of money?. What is Ashura’s share?
18. Using a number line, add -5 + -2
19. Arrange the numbers 0.35, ![]() , 50%, 25 and 0.33
, 50%, 25 and 0.33
20. A room with length 270cm and width 150cm is to be covered with square tiles. What is the largest size of the tiles to be used if no space of the room is to be left uncovered?
SECTION B: (40 Marks)
21. (a )A father is 24 years older than his son. After 2years, the father’s age will be three times that of his son. Find their present ages.
(b) The length of a rectangular park exceeds its width by 17m. If the perimeter of the park is 178m. Find the dimensions of the park.
- Solve the following simultaneous equations:
(a) 3x – y = 10
5x + 2y = 24
Use substitution method
(b) 3x + 4y = 17
5x – 2y = 11
Use elimination method
23. (a) The sum of three consecutive odd numbers is 51. Find the numbers
(b) A man gave ![]() of his money to his son,
of his money to his son, ![]() of the remainder to his daughter and the remaining to his wife. If his wife gets shs 8700, what was the total amount?
of the remainder to his daughter and the remaining to his wife. If his wife gets shs 8700, what was the total amount?
24. If 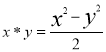 ,find (a)
,find (a) ![]() (b) find n if
(b) find n if ![]()
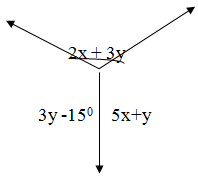
25. Use the two figures below to find the values of x and y
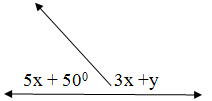
FORM ONE MATHEMATICS EXAM SERIES 11
FORM ONE MATHEMATICS EXAM SERIES 11
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
MID TERM EXAMIATIONS
024 MATHS- ONE
Duration: 2:30 Hours
Instructions
- This paper consists of two sections A and B.
- Answer all questions in all sections
- Show clearly all working for each question
SECTION A
- Write the following into expanded form a) 720902 b) 53901
- Write the place value of digits in the brackets
a) 985041 (0)
b) 324001 (2)
3. Express the following as the product of prime factors
a) 144 b) 208
4 a) Evaluate 96 – [ (15 – 3) – (45 – 15) ] x 10 +4
a) What percent of 2.8kg is 70g ?
5. Write the following in the form of a/b
a) 0.367
b) 06789
6 a) Represent 7/6 on a number line
b) b) Use number line to multiply -2 x 5
7. Change  into a)Decimal b) Fraction
into a)Decimal b) Fraction
8. Find LCM and GCF of 21, 28, 45 and 36
9. From a rope  m long, a piece of
m long, a piece of  m has been cut off. What is the length of the remaining piece?
m has been cut off. What is the length of the remaining piece?
11. Find value of y in the following equation 3y + 2 = 14
12. Find value of x in the below

13. If 85% of the workers in a factory are males and the number of female is 36. Find total number of workers in a factory.
14. Arrange the following numbers in ascending order
a) 0.07, -1, 5, -10, 0.5, 0.9
b) 
15. On increasing the price of an article by 6%, the price of an article becomes Sh. 1551. What was the original price of the article?
SECTION B
 16. If a – b=2, find value of 25 + 2b + 7 – 2a
16. If a – b=2, find value of 25 + 2b + 7 – 2a
3b – 3a
.
17. a) List all odd numbers between 20 and 40 which are not divisible by 3.
b) List all prime numbers between 1 and 20
18. A man is 35 years older than his son. 9 years ago he was six times as old as his son. What is their present age now?
19 Mashaka’s cow produces 19 litres of milk in one day. How many cows should mashaka keep so that he can sell 114 litres in one day? How much money did he get by producing 19 liters’ in a day if 200ml costs Sh. 150/= ?
20 Find dam dm cm
18 9 9
11 7 5

 + 31 1 4
+ 31 1 4
FORM ONE MATHEMATICS EXAM SERIES 8
FORM ONE MATHEMATICS EXAM SERIES 8
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256