FORM FOUR MATHEMATICS EXAM SERIES 221
FORM FOUR MATHEMATICS EXAM SERIES 221
THE OFFICE OF THE PRESIDENT, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT.
SECONDARY EXAMINATION SERIES
MARCH 2025
MATHEMATICS FORM FOUR
TIME: 2:30HRS
Instructions
- This paper will consist of sections A and B with a total of 14 questions
- Answer all questions in both sections A and B
- Section A will carry 60 marks and section B will carry 40 marks
- Mathematical tables/ Calculator may be used
- Write your Examination number on the top right corner of your answer booklet provided. Use R = 6400 and π= 3.14
SECTION A (60 MARKS)
1. (a) Write a number in which O represents hundreds, 7 represents ten thousands, 3 represents ones, 9 represents thousands, 6 represents hundred thousand and 8 represents tens.
(b) Convert and 360% to decimal, then approximate their products to one significant figure.
(c) 14 - [−2 − (8 ÷ 2) + 5]
2. (a) Express (7 + √2)2 in the form of a + b√c
(b) Find the value of x given that 2logx = log4 + log (2x − 3)
(c) Solve for y given that 125y+1 + 53y = 630
3. (a) In a class of 60 students, 40 students like History, 36 students like Geography, 24 students like both subjects. Find the number of students who like;
(i) history only
(ii) geography only
(iii) either history or geography
(iv) neither history nor geography
(b) When a fair die is tossed, find the probability that the number obtained is,
(i) more than five
(ii) at least one
(iii) at most six.
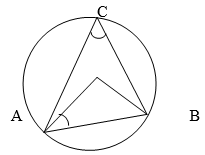
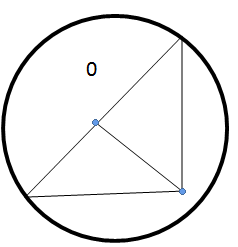
4. (a) In the figure below AB= 3cm, < BCA = 300 and <BDC = 90. Given that <ABC =<BDC
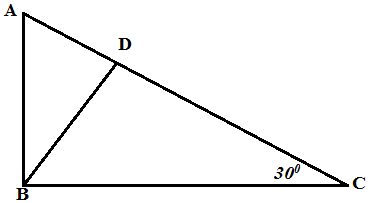
(i) Prove that ∆BDC ~ ∆ ABC
(ii) Calculate length BD
(b) Two concentric regular Hexagons are such that the radius of circle inscribing the larger on is twice that inscribing the smaller hexagon. If the radius of smaller is 5cm. find area between the two Hexagons.
5. (a) The value of “V” of a diamond is proportional to the square of its weight “W”. It is known that a Diamond weighing 10grams is worth Tsh 200,000/=
(i) Write down expression that relates V and W
(ii) Find the weight of a diamond that worth Tsh 5,000,000/=
(b) A day worker is paid Tsh 48,000/= for 16 hours work.
(i) What is the rate of payment?
(ii) At this rate, how much would he receive for 30 hours of work?
(iii) At this rate, for how long must he work in order to receive Tsh 120,000/=
6. (a) A students had two plant seedlings. She measured the rate at which the seedlings were growing. Seedling A grew 5 cm in 10 days and seedling B grew 8 cm in 12 days. Which seedling was growing more quickly?
(b)Suppose x varies directly as y square and inversely as p. if x=2, when y=3 and p=1, Find the value of y when x=4 and p=5.
7. (a) Kabujage Saved Tshs 6 million in a savings Bank whose interest rate was 100% compounded annually. Find the amount in Kabujages’s savings accounts after 5 years
(b) A small business sells products with 1,000,000tshs during its first year. The owner of the business has set a goal of increasing annual sales by Tshs 750,000 each year. Assuming this goal is met. Find the total sales during the first 10 years of the business in operation
8. a) Given that (Z + 1) is directly proportional to x and inversely proportional to the square root of y. If x =2 when y=4 and Z =4 find Z when X = 3 and y =9
(b) A bus travels 240 km using 16 litres of diesel. How many liters of diesel are needed to drive 90km?
9. (a) Solve the quadratic equation x2 – 8x +7 = 0
(b) A field is 10m longer than its wide. The area is 7,200m2. What is the width?
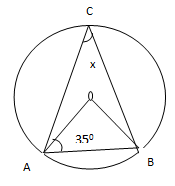
10. (a)In a class of 20 pupils, 12 pupils study English but not History, 4 pupils study History but not English and one pupils study neither English nor History. How many pupils in class study History? (Use Venn diagram)?
(b)Inside the class, there are 6 wooden chairs and 8 plastic, two chairs are taken at random from the class without replacement. By using tree diagram, find the probability that the first chair taken is wooden and the second chair is plastic.
FORM FOUR MATHEMATICS EXAM SERIES 207
FORM FOUR MATHEMATICS EXAM SERIES 207
PRESIDENT OFFICE REGIONAL ADMNISTRATION
AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
COMPETENCE BASED ASSEMENT
MATHEMATICS FORM FOUR
MID-TERM-AUG/SEPT – 2024
TIME: 3HOURS
INSTRUCTION
- This paper consists of two sections A and B with total of fourteen (14) questions
- Answer all questions
- Programmable calculators, phones and any other unauthorized materials are not allowed in examination room
- Write your examination on every page of your answer sheet provided
- All diagrams must be drawn in pencils
- All writings must be in black/blue ink
SECTION A. 60 MARKS
1. (a) Three brothers visit the grandfather at intervals of 5days, 7 days and 12 days. If they start together at 15th July. Then find the date that they will visit the grandmother together next time. (Each moths are 30 days)
(b) The total mass of cotton harvested in Ali’s district was 17452.225 kg. Round off this number to the nearest (i) Hundreds (ii) Thousandth.
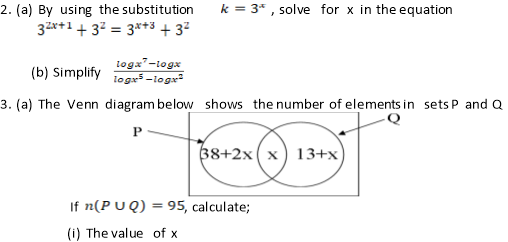
(ii) ![]()
(b) A letter is chosen from the word “RANDOM”. What is the probability that it is;
(i) n? (ii) A vowel
- (a) Find the equation of the line which is parallel to the line x +4y -1 = 0 and which passes through the point (4, -3)
-
 If and
If and  Find x and y given that
Find x and y given that
-
- In the following figure, a regular hexagon is inscribed in a circle.
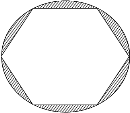
If the perimeter of the hexagon is 42cm. find
(i) the radius of the circle
(ii) the radius of the circle
(iii) the area of the circle and the regular polygon
- (a) In the preparation of Pepsi cola, a bottling filling machine can fill 1,500 bottles in 45
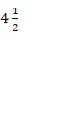 minutes. How many bottles will it fill in hours?
minutes. How many bottles will it fill in hours?
- The energy (E) stored in an elastic band varies as the square of the extension (x). When
the elastic band is extended by 4cm; the energy is 240Joules. What is the energy stored when the extension is 6cm? What is the extension when the stored energy is 60 Joules?
- (a) A car which its buying price was sh.12, 500,000 was sold at a loss of 40 percent. Find the loss made and selling price
- Given the following transactions
Sales for 2009. ......................................................................... 51,000/=
Stock at start. ............................................................................. 9,000/=
Purchases. ................................................................................. 34,650/=
Stock at close .............................................................................. 6,000/=
Returns on sales (inwards). .......................................................... 1,000/=
Return outwards (return on purchase). ............................................. 150/=
From the above transactions, deduce
(i) Cost of sales
(ii) Average stock
(iii) Rate of stock turn
(iv) Net sales (turnover)
- (a) How many integers are there between 14 and 1,000 which are divisible by 17?
(b) The 4th and 7th terms of a G.P are 144 and 18 respectively. Find
- The common ratio
- The first term
- The sum of the first six terms
- (a) A ladder reaches the top of wall 18m high where the other end on the ground is 8m from The wall. Find the length of the ladder,
(b)Verify that
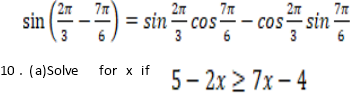
(b). The length of the sides of a right angled triangle is (2x+1) cm, (2x1) cm and xcm. Find x if 2x+1 is the hypotenuse
SECTION B (40 marks)
- (a) The following table shows the distribution of marks scored by 42 candidates in Mathematics exam at Kihesa Secondary School of Mock 2023.
| Marks (%) | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 |
| frequency | 7 | x | 11 | y | 4 | 2 |
Calculate
- The values of x and yif the Mode and the modal class is 53.75 and 50-55 respectively.
- The mean (use an assumed mean of the class mark within the modal class)
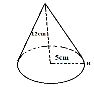
(b) Find the value of angles a and b in the figure below
![]()
![]()
![]()
- (a) The following rectangular prism represents a room 6m by 5m by 4m.
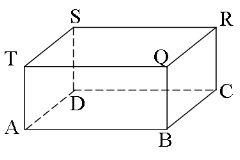
(i) Calculate the diagonal AR
(ii)Find the angle AR makes with the floor (iii) Find the total surface area
- Find the distance (in km) between towns P (12.450S, 30.50E) and Q (12.40S, 39.90E) along a line of latitude, correctly to 4 decimal places.
- (a) Find the value of k such that the matrix is singular 4
![]()
- The vertices of triangle ABC are A (1,2) B (3,1) and C (-2,1). If the triangle is reflected in the x –axis. Find the coordinates of the vertices of its image.
- Solve the following simultaneous equations by matrix method
![]()
-9x+8y – 1 = 0
- (a) A technical school is planning to buy two types of machines. A lather machine needs 3m2 of floor and a drill machine requires 2m2. The total space available is 30m2. The cost of one lather machine is 25,000 shillings, a drill machine costs 30,000 shillings and the school can spend not more than 300,000. Find the greatest number of machines the school can buy. (b) Given that
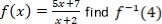
FORM FOUR MATHEMATICS EXAM SERIES 199
FORM FOUR MATHEMATICS EXAM SERIES 199
PRESIDENT’S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES,
MID TERM ONE – MARCH-2024
MATHEMATICS FORM FOUR
Time: 3Hours
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions in sections A and B
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA Mathematical tables and non-programmable calculator may be used.
6. All communication devices and any unauthorized materials are not allowed in the examination room.
7. Write your examination number on every page of your answer sheet(s).
SECTION A. (60 MARKS)
Answer all questions in this section.
- (a) Given the number 857636721. Write this number
- To the nearest thousands
- To hundreds
- In expanded form
(b) Three brothers visited their grandfather at interval of 5 days, 7 days and 12 days. If they started together on 15th July. Find the date they will visit the grandfather together next time. (Each month has 30days)
- (a) (i) Solve for X if
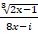 =16
=16
(ii) Simplify ![]()
(b) given that log 34 =1.262 and log 35=1.1465. Find log 3 0.8
- (a)In a class of 60 students, 40 students like history, 36 like geography, 24 students like both subjects. Find the number of students who like
- History only
- Either history or geography
- Geography only
- Neither history nor geography
(b) When a fair die is tossed, find probability that the number obtained is
- More than five
- At least one
- At most six
- If a=5i+4j, b= -3i+3j, and c = -2i+5j. find
- V= 3a+b-3c
- The magnitude of V
(b) given the point A (3,3) B (-3,1) C (-1,-1) and D (1,-7)
- Show the line through AB and CD are perpendicular to each other.
- Find the equation of the line through point (-4,5) which is parallel to BC
- (a) A school cow produces18 litres of milk every day. How many cows of same type should the school keep to get 126 litres of milk every day.
(b) One family from England traveled for holiday to France and exchanged 450 pounds for Euros when exchange rate was 1.41 Euros to Pound. They spent 500 Euros and then exchanged the remaining amount into pounds by that time the exchange rate had become 1.46 Euros to Pound. How much money remained in terms of pounds?
- (a) A school hall has 32 rows of seats. If there are 26 seats in the first row, 30 seats in 2nd row, 34 seats in 3rd row and so on. How many seats are there in a theatre?
(b) Mr Cuthbert starts an employment with a monthly salary of 340,000 and receives an increment of Tsh 12,000/= per year.
- What will be his salary in fourteen year of employment
- After how long will he earning Tsh 592,000 per month.
- (a) The fifth and eleventh terms of AP are 8 and -34 respectively. Find the sum of first ten terms.
(b) A school wishes to invest Tsh 100,000,000 in a bank which pays an interest rate of 2% compounded annually.
- Find total amount of money that will accumulate after 2years
- Calculate the interest after 2 years
- (a) Asha is three years older than her brother Juma. Three years to come the product of their age will be 130 years.
- Formulate the quadratic equation representing information above
- Use the quadratic equation formula to find present age of Asha and Juma
- Solve the equation by completing the square
2x2-3x-5=0
- What do the following terms mean as used in Accounts
- Cash book
- Asset
- Credit transactions
(b) A company bought two cars for Tsh 25,000,000/= each. If one car was sold at a profit of 18% and another was sold at a loss of 6%. In the whole transaction there was no loss. What was the profit made by the company?
- If the square of the hypotennce of an isosceles right angled Triangle is 128cm2. Find the length of each other sides.
(b) From the top of the tower, of height 60m the angle of depression of the top and the bottom of a building are observed to be 300 and 600 respectively. Find height of the building.
SECTION B. 40 MARKS
- (a) If matrix A is singular, what will be value of Y given that
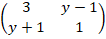
(b) Solve the following simultaneous equation by matrix method
2x+y=7
4x+3y=17
(c) Find the image of (3,5) after rotation of 2700 about the origin in the ant-clockwise direction.
- (a) A rectangular box with top WXYZ and base ABCD has AB= 9 cm, BC =12 cm, WA=3cm. calculate
- The length of AC
- The angle between WC and AC
- Consider the following frequency distribution table below.
| Marks | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 | 100-109 | 110-119 |
| frequency | 1 | 2 | 5 | 11 | 21 | 20 | 17 | 10 | 6 | 4 | 2 | 1 |
(a)Draw the histogram and use it to estimate the mode in one decimal place
(b) Find the value of angle x in the figure below
- (a) A function F is defined by the formula f(x) =
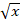 where x is a whole number.
where x is a whole number.
- If f(x) =25. Find the value of x
- Fund the value of
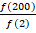
(b)A craftsman wishes to decide how many of each type A and B charcoal stove has to fabricate in order to maximize profit for the month. Unit profit for type A stove is 1000/= and 1500/= for type B. type A stove requires 1m2 of mild steel sheet per unit and type B 2m2 . He has only 12m2 of mild steel available. He can fabricate a total of 8 stoves of either type per month. How many stove of each type should be fabricated.
FORM FOUR MATHEMATICS EXAM SERIES 183
FORM FOUR MATHEMATICS EXAM SERIES 183
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
MID TERM EXAMINATION AUG- 2023
SECONDARY EXAMINATION SERIES
MATHEMATICS FORM FOUR
TIME: 3 HOURS AUG-2023
Instructions
- This paper consists of section A and B with fourteen (14) questions.
- Answer all questions.
- Each question in section A caries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- Mathematical tables and non – programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room
- Write your Examination number on every page of your answer booklet(s).
SECTION A (60 MARKS)
- (a) Simplify the sum of 85% of 9861 and
 of 12458. Write your answer correct to two significant figures.
of 12458. Write your answer correct to two significant figures.
(b) (i) Mr. Tumai Distributed Tshs 960,000/= awards to students who passed well in their examinations and their respective teachers as follow: 23% to all students who passed Arts Subjects. 15% to students who passed Mathematics and 27% to students who passed science subjects. The remained amount was distributed to teachers. Find the amount that were awarded to teachers.
(ii) Three bells commence tolling together and toll at intervals of 8, 10 and 12 seconds respectively. How many times do they toll together in 50 minutes?
- (a) If
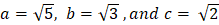 . Simplify
. Simplify 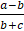
(b) Describe the applications of Logarithm in real life situations
- In a certain class MSUVA displayed counting numbers less than 30. From the displayed numbers, OKWI mentioned all numbers divisible by 2 and FEITOTO mentioned all numbers that were the multiples of 3.
- (i) Outline all numbers that were mentioned by OKWI and FEITOTO in common.
(ii) How many numbers were mentioned by either OKWI or FEITOTO?
- If a number was selected at random from the numbers displayed by MSUVA, what is the probability that a selected number was a multiple of 3?
- (a) Given that
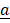 = 4i + 3j and
= 4i + 3j and 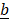 = 6i – 3j, find the value of “h” and “k” if h
= 6i – 3j, find the value of “h” and “k” if h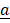 + k
+ k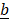 = 10i + j
= 10i + j
(b) A perpendicular line from the point P(2,-4) to the line meets the line at point Z(-1,3). Find:
i. Distance ![]()
ii. If the point Z(-1,3) is a mid-point of the line ![]() , find the coordinates of point
, find the coordinates of point ![]()
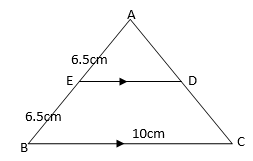
- (a) In the following figure;
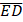 //
//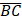 and
and 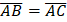 ; If
; If  and
and  , find the Area of BCDE
, find the Area of BCDE
(b) By considering the Alternating opposite angles theorem, draw the diagram hence identify the corresponding angles.
- (a) The time “t” taken to buy fuel at LAKE OIL PETROL STATION in Morogoro varies directly as the number of vehicle “V” in the queue and inversely as the number of pumps “P” available in the station. In petrol station with 10 pumps it takes 20 minutes to fuel 40 vehicles.
- Write vehicle “V” in terms of pumps “P” and time “t”
- Find the time it will take to fuel 60 vehicles in a station with 4 pumps.
(b) Mayele bought 3 bottles of juice of capacity 350 ml and Dialo bought 1 bottle of juice of capacity 1 litre.
i. Who had more juice to drink?
ii. How much more?
- (a) What do the following terms mean as used in Accounts?
- Cash book
- Assets
- Credit transactions
(b) A company bought two cars for Tshs 25,000,000/= each. If one car was sold at a profit of 18% and another was sold at a loss of 6%. In the whole transactions there were no loss. What was the profit made by a company?
- (a) A BODA BODA driver rates after each kilometre. The fare is Tshs. 1000/= for the first kilometre and raise by Tshs. 500/= for each additional kilometre. If BALEKE want to travel 10 kilometres by BODA BODA. What will he be charged by BODA BODA driver?
(b) The number 19683 is in which term in the following Geometric sequence; 3, 9, 27 …?
- (a) If the square of the hypotenuse of an isosceles right-angled triangle is 128 cm2 find
the length of each other sides
(b) From the top of a tower of height 60m the angles of depression of the top and the bottom of a building are observed to be 300 and 600 respectively. Find the height of the building.
- (a) If the length of each side of a square is increased by 6, the area become increased to 16 times the area of the small square. Find the length of one side of the original square.
(b) A large rectangular garden in a park is 120m wide and 150m long. A contractor is called in to add a brick walkway to surround this garden by the same width. If the area of the walkway is 2800m2, how wide is the walkway?
SECTION B (40 MARKS)
- (a) In certain research the data were summarized as shown in a table below:
| Class Mark | 10 | 15 | 20 | 25 | 30 | 35 |
| Frequency | 3 | 2 | 10 | 5 | 4 | 1 |
By using the data above reconstruct a frequency distribution table including class interval and frequency.
(b) Prove that equal chords of a circle subtend equal angles at a centre.
- (a) Two towns P and Q on the Latitude 480 are 370 Nautical miles apart. Find the
difference in their longitude.
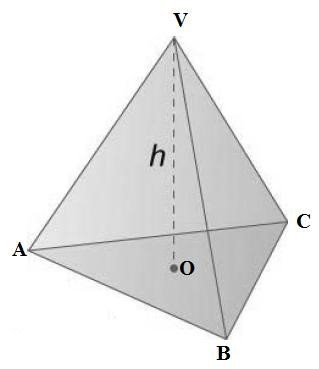
(b) A pyramid with vertex V and edges VA, VB, VC, VD each 15cm long has a rectangular base ABCD where AB = CD = 10cm and AD = BC = 8cm.
i. Sketch the pyramid using the above information.
ii. Calculate the height “VO” of the pyramid where “O” is the centre of the rectangle.
- Calculate the angle between the base and edge
- (a). (i). Find the possible values of x if the matrix
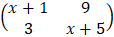 has no inverse.
has no inverse.
(ii). By using matrix method, solve the equations ![]()
(b). A transformation is given ![]()
![]() and
and ![]() , find the image of the equation 2x – 3y = 6 under the transformation matrix which performs the above transformations.
, find the image of the equation 2x – 3y = 6 under the transformation matrix which performs the above transformations.
- (a) A function f is defined as;
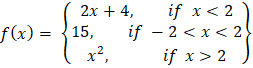
Find (i) f(1.95) (ii) f(15) (iii) Domain of f (iv) identify the type of a function f
(b) A school is preparing a trip for 400 students. The company who is proving the
transportation has 10 buses of 50 seats each and 8 buses of 40 seats, but only 9 drivers available. The rental cost for a large bus is 800,000/= and 600,000/= for the small bus. How many buses of each type should be used for the trip for the least possible cost?
Page 1 of 6
FORM FOUR MATHEMATICS EXAM SERIES 172
FORM FOUR MATHEMATICS EXAM SERIES 172
PRESIDENT OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS
FORM FOUR
TERMINAL EXAMINATION - MAY, 2023
TIME 3:00 HOURS
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in section A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your examination number on every page of your answer booklet(s)
SECTION A (60 Marks)
Answer all questions in this section.
1. ![]()
![]()
![]()
![]()
![]()
2. ![]()
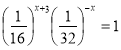
![]()
3. (a) A box contains 4 white balls and 5 black balls. Two balls are selected at random without replacement. Find the probability that
(i) Both are white balls
(ii) The first is black and the second is the white ball
(b) In a class of 15 students who take either Mathematics or Biology, 12 students take Mathematics, 8 students take Biology. If each student takes either subjects find by using formula the number of students who take Biology but not Mathematics.
4. (a) The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
(b) The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
5. (a) The area of the triangle ABC is 140 cm2, AB = 20, AC = 14cm, find the angle BAC
(b) Triangle XYZ is similar to triangle ABC and XY = 8 cm. If the area of the triangle XYZ is 24 cm2 and the area of the triangle ABC is 96 cm2. Calculate the length of AB.
6.![]()
![]()
![]()
![]()
![]()
7. ![]()
![]()
![]()
![]() =
=
![]() /=
/=
19 bought Shelves for cash 110,000/=
20 sold goods for cash 900,000/=
21 purchases goods for cash 800,000/=
22 sold goods for cash 1, 400,000/=
26 paid rent 300,000/=
Record the above transactions in Cash account ledger and extract a Trial balance.
8. (a). The product of a three terms of a geometric progression (GP) is 8000. If the first term is 4. Find the second term and third term
(b). Mahona invested a certain amount of money in a Savings Bank whose interest rate was 10% compounded annually. After two years he got 5000 shillings.
- How much did he invest at the start?
- How much did he receives as Interest at the end of two years.
9. (a) Find the value of
Sin (1500) cos (3150) Without using mathematical tables
Tan (3000)
(b) Calculate the angles of a triangle which has sides of lengths 4m, 5m and 7m
10. (a). Given that x2 –y2 = 27 and x + y = 9 find the value of xy
(b). Solve the equation 2x2 – 3x – 5 = 0 by completing the square.
SECTION B (40 Marks)
Answer all questions
11. (a) The number of workers absent in 52 working days is given in a cumulative frequency table below
| No.of absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 - 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find (i) Percentage of workers who are absent at least for 20 days
(ii) Median
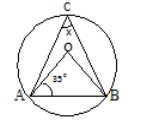
(b) Find the angle x in the figure below
12. (a) A ship sails from point A (40![]() ) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and
) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and ![]() (give your answer in nearest degree)
(give your answer in nearest degree)
(b) VABCD is a pyramid with VA=VB=VC=VD=5cm and ABCD is a square base of sides 4cm each. Assume that the centre of the base is at point N. Find
- The angle between VA and the base ABCD
- The volume of the pyramid
13. ![]()
![]()
![]()
![]()
![]()
14. (a). A function F is defined by the formula f(x) = ![]() where x is a whole number
where x is a whole number
- If f(x) = 25 find the value of x
- Find the value of
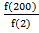
(b). A craftsman wishes to decide how many of each type A and B charcoal stove he has to fabricate in order to maximize profit for this month. Unit profit for type A stove is shs. 1000 and Unit profit for type B is shs. 1500. Type A stove requires 1m2 of mild steel sheet per unit and type B requires 2m2. He has only 12 m2 of mild steel available. He can fabricate a total of 8 stoves of either type per month. How many of each type should he fabricate?
FORM FOUR MATHEMATICS EXAM SERIES 157
FORM FOUR MATHEMATICS EXAM SERIES 157
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCY BASED SECONDARY EXAMINATION SERIES
BASIC MATHEMATICS
FORM FOUR- SEPT 2022
INSTRUCTION
- This papers consist of sections A and B with a total of fourteen (14) questions
- Answer all questions
- Each question A carries six (06) marks while each question in section B carries ten (10) marks
- All necessary working and answers for each question must be shown clearly
- Mathematical table and non-programmable calculators may be used
- All communication devices and any unauthorized materials are NOT allowed in the examination room
- Write your examination number on every page of your answer booklet(s)
SECTION A: (60 MARKS)
Answer all questions in this section
- (a)Round each of the numbers x=2.354, y=4.843 and z=1.789 to one decimal place and then use the results obtained to find the value of A to two significant figures given that
![]()
![]() If k=0.5
If k=0.5![]() and P=0.8
and P=0.8![]() , find the value of
, find the value of ![]()
- (a)Use the substitution = 2y to solve the equation 22+1 – 2y+2 + =2y
(b)Find the solution set of the system
![]()
- (a)In a class of 40 students, each must take at least one of the subject either mathematics or Additional mathematics. If 25 students take mathematics and 20 Additional mathematics,
Determine
- The number of those who take both subjects
- The number of those who take mathematics but not Additional mathematics
(b)(i) What do the mutually exclusive events mean as used in probability?
(ii))Find the probability of obtaining a 3 or 5 in one roll of a die
- (a)Given two lines 5x + 6y=5 and kx – 3y=10, find the value of k if the lines are;
- Perpendicular
- Parallel
(b)Given vectors ![]() calculate,
calculate,
(i) ![]() (ii) |w|w
(ii) |w|w
- (a)Two triangles are similar. The ratio of their corresponding sides is 4:5. If the area of the first triangle is 20cm2, find the area of the second triangle.
(b)The interior angle of regular polygon is 120° greater than the exterior angle. Find the number of sides of the polygon and hence identify the name of the polygon.
- (a)Mr. Haruna bought a car from Japan worth 5,900,000 Japanese Yen. When he arrived in Tanzania he was charged custom duty of 25% on the car. If the exchange rate were as follows
1 us dollar = 118 Japanese Yen
1 us dollar = 76 Tanzanian shillings
Calculate the total cost of buying a car including the charged custom duty of 25% in Tanzania shillings.
(b) The number of eggs which a goose lays in a week varies as the cube root of the average number of hours of sleep she has. When she has 8 hours sleep, she lays 4 eggs. How long does she sleep when she lays 5 eggs?
- (a)Moses sold his computer for sh. 2,430,000 and result lost 20% of the price he paid for it.
- How much did he pay for the computer/
- What was the loss he incurred
(b)(i)The ratio of boy to girls at Mtakuja secondary school is 3:7. If the school has 500 students, find the number of boys at the school.
(ii)Define the term trial balance as used in Accounts and write one uses of it.
- The third, the fourth and eight terms of arithmetic progression (A.P), forms the first three consecutive terms of a geometric progression (G.P). If the sum of the first ten terms of the A.P is 85. Calculate
- The first terms of both the A.P and the G.P
- The common ratio
- The sum of the first 5 terms of the GP
- (a) Given that
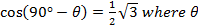 is an acute angle, without using tables, find the value of
is an acute angle, without using tables, find the value of 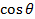
(b)A building has an angle of elevation of 35° from point P, and angle of the elevation of 45°from a point Q. if the distance between points P and Q is 30cm, what is the height of the building (Write your final answer to the nearest whole number)
- (a)Solve for if
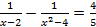
(b)Find two consecutive numbers such that the sum of their squares is equal to 145.
SECTION B: (40 Marks)
Answer all questions in this section
- (a)The examination score of 33 students are given on the following cumulative frequency table.
| Class interval | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Cumulative frequency | 2 | 4 | 9 | 17 | 29 | 33 |
- Find the mean score
- Find the median and median class
- Find the mode and the modal class
(b)Show that the radius of a circle with an arc of a length ![]() m and central angle
m and central angle ![]() is 6m
is 6m
- (a)(i) Calculate the volume of a right cylinder whose base radius is 18cm, and the height is 14cm (Use
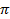 = 3.142) (ii)Calculate the total surface area of a right circular cone below, whose base radius is 5cm and whose height from the vertex to the centre is 12cm. (Use
= 3.142) (ii)Calculate the total surface area of a right circular cone below, whose base radius is 5cm and whose height from the vertex to the centre is 12cm. (Use 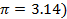
(b)Calculate the distance from Ruvuma (15°S, 45°E) to Mtwara (15°S, 49E) in km. use ![]() and the diameter of the earth as 12800km and the answer should be correct to two decimal places.
and the diameter of the earth as 12800km and the answer should be correct to two decimal places.
- (a)Determine the Matrix A from the equation
![]()
(b)A liner transformation maps the point (x,y) onto (x' y') where x'=4x + 3y and y'=x – 2y. Find
- The matrix T
- Inverse of the matrix T
- The image of a point (5,3) under T
- (a)If f(x) = x2 – 4x+3
Find (i) f-1 (x)
(ii) the domain and range of f(x)
(b)A shopkeeper buys two types of sugar, White sugar and brown Sugar. The white sugar is sold at shs 40,000/= per bag and the brown sugar is sold at shs 60,000/= per bag. He has shs 1,500,000/= available and decides to buy at least 30 bags altogether. He has also decides that at least one third of 30 bags should be brown sugar. He buy x bags of white sugar and y bags of brown sugar.
- Write down three (3) inequalities which will summarize the above information.
- Represent these inequalities graphically
- The shopkeeper makes a profit of shs 10,000/= from a bag of white sugar and shs 20,000/= from a bag of brown sugar. Assuming he can cell his entire stock, how many bags of brown sugar. Assuming he can cell his entire stock, stock, how many bags of each type should he buy to maximize his profit? Find that profit.
FORM FOUR MATHEMATICS EXAM SERIES 120
FORM FOUR MATHEMATICS EXAM SERIES 120
OFFICE OF THE PRESIDENT, MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
TERMINAL EXAMINATIONS- MAY 2022
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a) By using mathematical table evaluate ![]() to three significant figures taking
to three significant figures taking ![]()
(b)If ![]() Find Z = x + y hence express Z as fraction in its lowest form.
Find Z = x + y hence express Z as fraction in its lowest form.
2(a) Simplify ![]()
(b)Solve the equation ![]()
3.(a)Given ![]() then find
then find ![]()
(b)In class of 25 students, 12 students have taken mathematics, 8 have taken Biology. Represent this information on the Venn diagram hence or otherwise find number of students who.
- Have taken mathematics and biology
- Biology but not mathematics
4(a)If Alice deserves twice as many marks as Brenda and Brenda deserve half as much as many marks as Catherine, how many marks does each deserve when their total marks are 125.
(b)Given the vector ![]() determine;
determine;
- The value of k such that
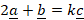
- A unit vector parallel to
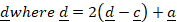
5(a)The radius of the circle which inscribe an equilateral triangle is 2cm, find the perimeter of the triangle correct to two decimal places.
(b)In the diagram below O is the centre and ![]() is the diameter of the circle
is the diameter of the circle ![]() If
If ![]() and
and ![]() Find the size of the angles of Quadrilateral ABCD
Find the size of the angles of Quadrilateral ABCD
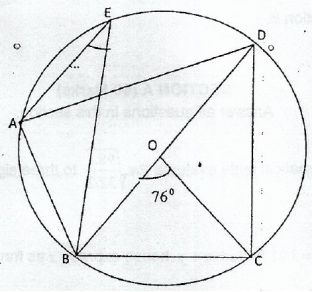
6(a)The mass of a plastic disc is inversely proportional to its area. If a disc of area 180cm2 has a mass of 200g
- Write down the equation relating mass (M) and area(A) of a disc.
- If a similar disc has mass of 250g what is its area?
(b)Given ![]() make t the subject of the formula
make t the subject of the formula
7.(a) If ![]() determine
determine ![]()
(b)The sides of the rectangle are in the ratio 4:5. Given that the area of this rectangle is 20cm2. Find the dimension of the rectangle.
8(a)The seventh term of a geometric progression is eighth times the fourth term and the fifth term is 48, find the term and the common ratio.
(b)A display of beef masala in supermarket is to have the form of a pyramid with 20 cans in the bottom row, 19 on the next row, 18 cans on the next row, and so on, with a single can at the top. How many cans of beef masala will be required for the display?
9.(a)If A and B are two complementary angles and ![]() find
find ![]() hence use the results to verify that
hence use the results to verify that ![]()
(b)A man 12m directly away from a tree and from this position the angle of elevation of the top of the tree is 24°. If the measurement is taken from a point 1.5m above the ground level, find the height of the tree.
10(a)By completing the square solve the quadratic equation ![]()
(b)Given ![]() Find
Find
- The value of a and b
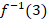
SECTION B (40 MARKS)
Answer Any Four Questions from this section
11.One end of the rectangular tank of length 6m is a square ![]() of side 2m. If AP is a diagonal of the tank, calculate;
of side 2m. If AP is a diagonal of the tank, calculate;
- AP correct one decimal places
- The angle between AP and the plane ABCD
- The surface area of the tank.
12.From a linear programming problem the following graph is draw
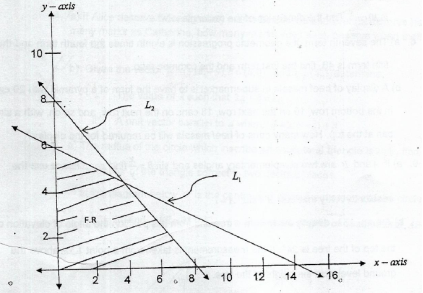
From the graph
- Find the equation of lines L1 and L2
- Write down the four inequalities representing the shaded region
- Determine the corner points of the feasible region
- Maximize the objective function
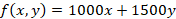 subjected to constraints in (ii)above
subjected to constraints in (ii)above
13.The number of workers in 52 working days is given in a cumulative frequency table below.
| Number of absences | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find;
- The percentage of workers who are absent at least 20days
- Mean, use assumed mean A=17
- Median
14.The following information relates to Mr. Mtipanga a trade as 31st December, 2011
Net profit 2,000,000/=
Cost of sales 60% of sales
Purchases 8,000,000/=
Closing stock 20% of purchase
Sales to Net profit ratio 10:1
Determine
- Sales
- Cost of sales
- Closing stock
- Opening stock
- Expenses
15.(a)Find the image of the point (1, -5) after reflection on the line x=0, and then translated by a vector a= (0, -6)
(b)![]() find two values of k such that
find two values of k such that ![]()
(c) Find the inverse of matrix ![]() hence use the results to solve the system of equations
hence use the results to solve the system of equations![]()
16(a)A bag contains 24 tennis balls, some white and some green. If a ball is chosen at random the probability of getting a green ball is ![]() . How many white balls are there?
. How many white balls are there?
(b)The probability that it’s raining at 8:30am on any one day is ![]() The probability that a boy wears a rain coat as he leaves for school at 8:30am is
The probability that a boy wears a rain coat as he leaves for school at 8:30am is ![]() if it rain at any time. If it is not raining the probability that he wear a coat is
if it rain at any time. If it is not raining the probability that he wear a coat is ![]() . What is the probability that he wear a coat on any one day?
. What is the probability that he wear a coat on any one day?
FORM FOUR MATHEMATICS EXAM SERIES 93
FORM FOUR MATHEMATICS EXAM SERIES 93
OFFICE OF THE PRESIDENT, MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
TERMINAL EXAMINATIONS- MAY 2022
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions.
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a) By using mathematical table evaluate ![]() to three significant figures taking
to three significant figures taking ![]()
(b)If ![]() Find Z = x + y hence express Z as fraction in its lowest form.
Find Z = x + y hence express Z as fraction in its lowest form.
2(a) Simplify ![]()
(b)Solve the equation ![]()
3.(a)Given ![]() then find
then find ![]()
(b)In class of 25 students, 12 students have taken mathematics, 8 have taken Biology. Represent this information on the Venn diagram hence or otherwise find number of students who.
- Have taken mathematics and biology
- Biology but not mathematics
4(a)If Alice deserves twice as many marks as Brenda and Brenda deserve half as much as many marks as Catherine, how many marks does each deserve when their total marks are 125.
(b)Given the vector ![]() determine;
determine;
- The value of k such that
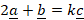
- A unit vector parallel to
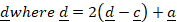
5(a)The radius of the circle which inscribe an equilateral triangle is 2cm, find the perimeter of the triangle correct to two decimal places.
(b)In the diagram below O is the centre and ![]() is the diameter of the circle
is the diameter of the circle ![]() If
If ![]() and
and ![]() Find the size of the angles of Quadrilateral ABCD
Find the size of the angles of Quadrilateral ABCD

6(a)The mass of a plastic disc is inversely proportional to its area. If a disc of area 180cm2 has a mass of 200g
- Write down the equation relating mass (M) and area(A) of a disc.
- If a similar disc has mass of 250g what is its area?
(b)Given ![]() make t the subject of the formula
make t the subject of the formula
7.(a) If ![]() determine
determine ![]()
(b)The sides of the rectangle are in the ratio 4:5. Given that the area of this rectangle is 20cm2. Find the dimension of the rectangle.
8(a)The seventh term of a geometric progression is eighth times the fourth term and the fifth term is 48, find the term and the common ratio.
(b)A display of beef masala in supermarket is to have the form of a pyramid with 20 cans in the bottom row, 19 on the next row, 18 cans on the next row, and so on, with a single can at the top. How many cans of beef masala will be required for the display?
9.(a)If A and B are two complementary angles and ![]() find
find ![]() hence use the results to verify that
hence use the results to verify that ![]()
(b)A man 12m directly away from a tree and from this position the angle of elevation of the top of the tree is 24°. If the measurement is taken from a point 1.5m above the ground level, find the height of the tree.
10(a)By completing the square solve the quadratic equation ![]()
(b)Given ![]() Find
Find
- The value of a and b
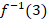
SECTION B (40 MARKS)
Answer Any Four Questions from this section
11.One end of the rectangular tank of length 6m is a square ![]() of side 2m. If AP is a diagonal of the tank, calculate;
of side 2m. If AP is a diagonal of the tank, calculate;
- AP correct one decimal places
- The angle between AP and the plane ABCD
- The surface area of the tank.
12.From a linear programming problem the following graph is draw

From the graph
- Find the equation of lines L1 and L2
- Write down the four inequalities representing the shaded region
- Determine the corner points of the feasible region
- Maximize the objective function
 subjected to constraints in (ii)above
subjected to constraints in (ii)above
13.The number of workers in 52 working days is given in a cumulative frequency table below.
| Number of absences | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find;
- The percentage of workers who are absent at least 20days
- Mean, use assumed mean A=17
- Median
14.The following information relates to Mr. Mtipanga a trade as 31st December, 2011
Net profit 2,000,000/=
Cost of sales 60% of sales
Purchases 8,000,000/=
Closing stock 20% of purchase
Sales to Net profit ratio 10:1
Determine
- Sales
- Cost of sales
- Closing stock
- Opening stock
- Expenses
15.(a)Find the image of the point (1, -5) after reflection on the line x=0, and then translated by a vector a= (0, -6)
(b)![]() find two values of k such that
find two values of k such that ![]()
(c) Find the inverse of matrix ![]() hence use the results to solve the system of equations
hence use the results to solve the system of equations![]()
16(a)A bag contains 24 tennis balls, some white and some green. If a ball is chosen at random the probability of getting a green ball is ![]() . How many white balls are there?
. How many white balls are there?
(b)The probability that it’s raining at 8:30am on any one day is ![]() The probability that a boy wears a rain coat as he leaves for school at 8:30am is
The probability that a boy wears a rain coat as he leaves for school at 8:30am is ![]() if it rain at any time. If it is not raining the probability that he wear a coat is
if it rain at any time. If it is not raining the probability that he wear a coat is ![]() . What is the probability that he wear a coat on any one day?
. What is the probability that he wear a coat on any one day?
FORM FOUR MATHEMATICS EXAM SERIES 92
FORM FOUR MATHEMATICS EXAM SERIES 92
PRESIDENT�S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAM SERIES
FORM 4 BASIC MATHEMATICS
SECTION A (60 MARKS)
Answer ALL questions in this section
1(a)Express the number 0.000038583
- In standard form
- Correct to 4 significant figures
(b)Change ![]() into fraction
into fraction
2(a)Solve the following equation simultaneously:
![]()
(b)Rationalize the denominator of the expression ![]()
3(a)Solve the following equations simultaneously
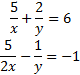
(b)Given ![]() . Find:
. Find: ![]()
4(a)Find the equation of the perpendicular bisector of the points A(4,8) and B (-4,-6)
giving your answer in the form ![]()
(b)Given that ![]() .
.
Find the relation between the three vectors a, b and c
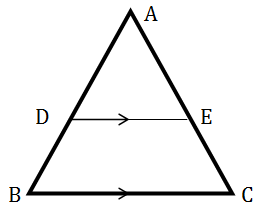
5. In the figure below ![]() //
//![]() and
and ![]()
If the area of DECB is 21cm2; find the area of ![]()
6(a) Given that w is directly proportional to x2 and inversely proportional to t and that
w=12 when x=2 and t=2. Find the value of w when x=3 and t=3
(b)Sophia and Alex had each Tsh.10,000. If Sophia wanted to buy the South African Rand and Alex wanted to buy the Malawian Kwacha, how much would each one receive?
(1 Rand =210 Tanzania shillings; and 1 Malawian Kwacha=10.80 Tanzanian shillings)
7(a)Given that A:C=10:7 and B:C=5:14; Find A:B
(b)Anna paid Tsh. 20,000 for 10 books. She sold ![]() of them at Tsh. 3,000 each and the remaining at Tsh. 3,500each. What was her percentage Loss or percentage profit?
of them at Tsh. 3,000 each and the remaining at Tsh. 3,500each. What was her percentage Loss or percentage profit?
8.(a)The sum of three terms which are in G.P is 28 while the product of these terms is 512.
Find the largest term.
(b)The fourth and sixth terms of an arithmetic progression are 45 and 55 respectively. Find;
- The first term
- The tenth term
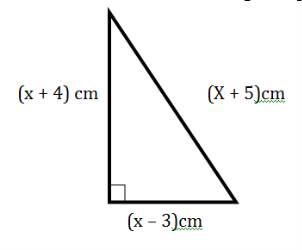
9.(a)Find value of x in the following triangle and hence find the area of the triangle.
(b)It is known that ![]() , find the relationship between
, find the relationship between ![]()
10(a)Factorize![]()
(b)Find the only solution of the equation ![]()
SECTION B (40 MARKS)
Answer any four (4) questions from this section
11(a)The following graph shows the feasible region of a linear programming problem where the shaded region is the feasible region. Study the graph and answer the questions that follow.
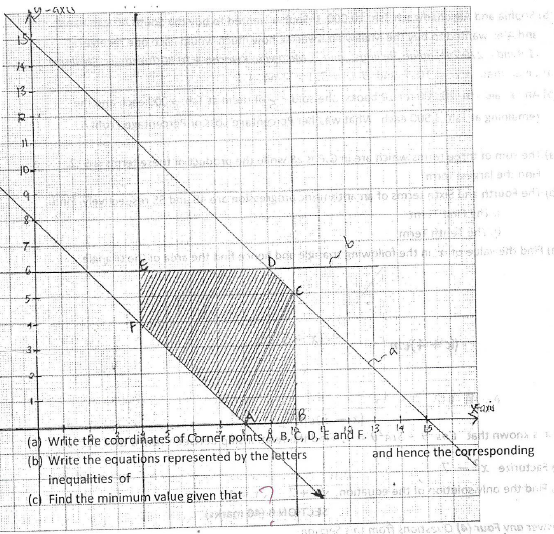
- Write the coordinates of Corner points A, B, C, D, E, and F
- Write the equations represented by the letters and hence the corresponding inequalities of
- Find the minimum value given that
12. The following frequency distribution table shows scores of marks of 50 students in a Mathematics Test:
| CLASS INTERVAL | 1.0 � 2.0 | 2.0 � 3.0 | 3.0 � 4.0 | 4.0 � 5.0 | 5.0 � 6.0 | 6.0 � 7.0 |
| FREQUENCY |
Calculate the measures of central Tendency
13(a) Town X and Y are located at (60�N, 30�E) and (60�N, 45�W) respectively on the earth�s surface. Calculate the distance between the two towns in Kilometers.
(b)Find the value of the angles marked X and Y in the figure below, given that O is the center of the circle.
(c)Find the area of a prism (rectangular) with l=8cm, w=6cm and h=4cm
14.from the balances given below, prepare a balance sheet at 31st December 2010. Capital shs 205,000; Furniture shs.54,000; cash in hand shs 16,000; Net profit sh.74,000; Motor van sh 30,000; stock sh. 110,000; Drawings shs. 24,000; shop fittings shs 20,000; loan from Bank sh. 80,000; Debtors shs. 180,000; Creditors shs.45,000 and Bank Overdraft shs. 30,000
15.(a)Use the inverse of matrix B to find matrix A given that;
![]()
(b)Write two conditions fr a transformation to be a linear.
(c)By using a sketch and not otherwise, find the image of P(3, 4) when rotated about 90� anticlockwise followed by another rotation of 180� clockwise.
16.(a)The ordered pairs of a Quadratic function f are ![]() Find the function f(x)
Find the function f(x)
(b)A fair die is tossed once. Find the probability that an even number or a prime number occurs
(c) Given that ![]()
1
FORM FOUR MATHEMATICS EXAM SERIES 82
FORM FOUR MATHEMATICS EXAM SERIES 82
THE UNITED REPUBLIC OF TANZANIA
PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM FOUR MID TERM EXAMINATION-2021
041 BASIC MATHEMATICS
Time: 3 Hours AUG, 2021
Instructions
- This paper consists of section A and B with a total of fourteen (14) questions
- Answer all questions in sections A and B, each question in section A carries six (6) marks while each question in section B carries ten (10) marks
- NECTA Mathematical tables may be used
- Cellular phones, calculators and any unauthorized materials are not allowed in the examination room
- Write your examination number on every page of your answer sheet (s)
SECTION A (60 MARKS)
Answer all questions in this section
- (a) Simplify
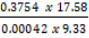 without using mathematical table express your answer in four significant figures.
without using mathematical table express your answer in four significant figures.
(b) Jenk and Jemry are riding on a circular path. Jenk completes a round in 24 minutes where as Jemry completes a round in 36 minutes. If they started at the same place and time and go in the same direction, after how many minutes will they meet again at the starting point?
- (a) Use mathematical table to evaluate
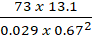
(b) Find the value of x and y if ![]() = 2025
= 2025
- (a) Let U be a universal set and A and B be the subsets of U where
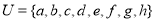 ,
, 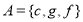 and
and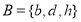 .
.
- Find the number of subsets of set A’
- Find
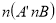
- If an element is picked at random from the universal set (u), find the probability that it is an element of set B
(b) Find the probability that a king appears in drawing single card from an Ordinary deck of 52 cards
- (a) The coordinate of P, Q and R are (2, m), (-3, 1) and (6, n) respectively. If the length of PQ is
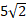 units and midpoint of QR is
units and midpoint of QR is 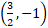 find the possible value of m and n
find the possible value of m and n
(b)The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
 (a) if
(a) if 
 and angle ABD =
and angle ABD = 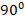 Calculate the length
Calculate the length 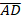
(b) (i) Given ![]() =
= ![]() =
= ![]() = 3 where
= 3 where ![]() ,
,![]() and
and ![]() are the sides of the triangle ABT and
are the sides of the triangle ABT and ![]() ,
,![]() and
and ![]() are the sides of the triangle KLC. What does this Information imply?
are the sides of the triangle KLC. What does this Information imply?
(ii) A regular Hexagon is inscribed in a circle if the perimeter of the hexagon Is 42cm, find the radius of the circle and its Area
- (a) If y varies inversely as
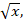 and x is multiplied by n. What is the ratio of the first y to the second y?
and x is multiplied by n. What is the ratio of the first y to the second y?
(b) The headmaster has enough food to last for his 600 students for 20 days from tomorrow. If 120 students leave the school today for UMISSETA game, how long will the food last?
- (a) By selling an article at shs 22,500/= a shopkeeper makes loss of 10%. At what price must the shopkeeper sell the article in order to get a profit of 10%?
(b) The following trial balance was extracted from the books of Nzilandodo on 31st December 2005.
TX MARKET LTD
TRIAL BALANCE AS AT 31.12.2005
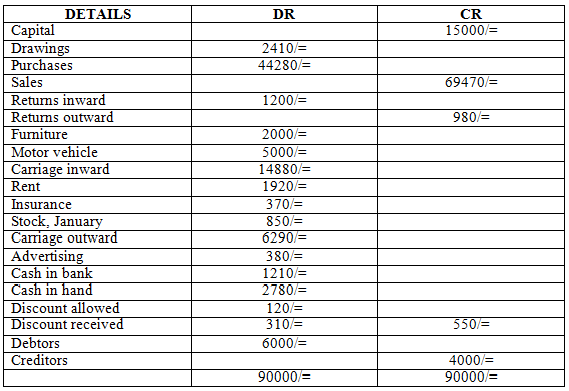
Note: Stock at close 31st December 7360. Required, prepare balance sheet as that date.
- (a) The sum of the first six terms of an A.P is 72 and the second term is seven times the fifth term.
- Find the first term and the common difference
- Find the sum of the first ten terms
(b) Find the sum of the first four terms of a geometric progression which has a first term of 1 and a common ratio of ![]()
- (a) If tan A =
 , where A is an obtuse angle,
, where A is an obtuse angle,
Find (i). Cos A + Sin A (ii). – Cos2 A – Sin2 A
(b) A and B are two points on the ground level and both lie west of flagstaff. The angle of elevation of the top of the flagstaff from A is 560 and from B is 430. If B is 28m from the foot of the flagstaff. How far apart are the points A and B?
- (a) Solve the quadratic equation x2 – 8x +7 = 0
(b) A field is 10m longer than its wide. The area is 7,200m2. What is the width?
SECTION B (40 marks)
Answer all questions in this section
- ( a) Consider the following frequency distribution tale below;
| Marks | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 | 100-109 | 110-119 |
| Freq | 1 | 2 | 5 | 11 | 21 | 20 | 17 | 10 | 6 | 4 | 2 | 1 |
Draw the histogram and use it to estimate the mode in one decimal place.
b) Find the value of angle X in the figure below.
- (a) A rectangular box with top WXYZ and base ABCD has AB=9cm, BC=12cm and WA = 3cm

Calculate (i) The length AC (ii) The angle between WC and AC
(b) Two places P and Q both on the parallel of latitude ![]() N differ in longitudes
N differ in longitudes
by ![]() find the distance between them along their parallel of latitude.
find the distance between them along their parallel of latitude.
- (a) If matrix A is singular, what will be the value of y given that
![]()
(b) Solve the following simultaneous equation by matrix method
2x + y = 7
4x+3y = 17
(c) Find the image of (3, 5) after rotation of 270o about the origin in anticlockwise direction.
- (a) If f(x) is the function such that
f(x)=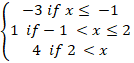
- Sketch the graph of f(x)
- State the domain and range of f(x)
(b) A transport company is hired to transport 420 people it has two types, P and Q of vehicle to be used. Type P carries 35 passengers and type Q carries 14 passengers. There are at least 10 vehicles of type Q and not more than 9 vehicles of type P. Write down inequalities to represent this information.
1 of 5
FORM FOUR MATHEMATICS EXAM SERIES 64
FORM FOUR MATHEMATICS EXAM SERIES 64
THE PRESIDENT�S OFFICE MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
COMPETENCE BASED SECONDARY EXAMINATION SERIES
FORM FOUR BASIC MATHEMATICS� TERMINAL� EXAMINATION
Time: 3 Hours Year: 2021
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions.
2.Answer all questions in sections A and B.
3.Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
5.NECTA mathematical tables and non-programmable calculator may be used.
6.All communication devices and any unauthorized materials are not allowed in the examination room.
7.The following constants for your calculations
Radius of the Earth =6370km,�� ![]() �
�
SECTION A (60 Marks) �
Answer All Question In This Section
1.(a) Calculate without using Mathematical tables, correct to two decimal places
![]() �
�
(b) Each student of Leo academy belongs to one club. ![]() �are members in drama club.
�are members in drama club. ![]() �are members in mathematics club and the number of science club is twice that of drama club .The rest are members of research club. What fraction of students are members of research club? 2. (a) Make x subject of the formula
�are members in mathematics club and the number of science club is twice that of drama club .The rest are members of research club. What fraction of students are members of research club? 2. (a) Make x subject of the formula
 �
�
(b)Three variables p, q and r are such that p varies directly as q and inversely as square of r. When p=9, q=12 and r=2. Find p when q=15 and r=5.
3.(a) ) Given that� ![]() ��and�
��and� ![]() ,� where X is an integer. Represent this in a venn diagram, hence find elements of: �
,� where X is an integer. Represent this in a venn diagram, hence find elements of: �
(i)AuB
(ii)AnB�
�(b) In a school of 95 pupils, 42 of the pupils take Biology but not Chemistry, 32 take both subject and 10 of them take Chemistry but not Biology. How many pupils do not take either Biology or Chemistry?
4.(a) Let P and Q be two points at (2,5) and (4, -1) respectively. Find
(i)Find equation of the line that passes through the midpoint of PQ and is perpendicular to it in form of ax + by +c=0
(ii)The distance between P and Q
�(b) A chord is 6cm from the center of a circle with radius 10cm. What is the length of a chord?
5.(a) In triangle PQR, PR=5cm, PQ=6cm and�
(i)The length of side QR
(ii) (b) The size of the exterior angle of a regular polygon is 450. Find (i)The number of sides (ii)The sum of all interior angles. 6.(a) Given t=3x , by using the substitution solve the equation� 32(1+x) - 3x =3(x+3) - 3 (b) A shopkeeper makes a profit of 40% by selling an article for T.Sh. 63,000/=. What would be his percentage loss if he sold the article for T,Sh. 40,000/= 7.(a) Prepare the balance sheet for the balances given below Capital 4,500,000/= Drawings 800,000/= Creditors 430,000/= Closing stock 500,000/= Debtors 800,000/= Buildings 1,600,000/= Motor Van 800,000/= Bank 400,000/= Cash 900,000/= Net profit 270,000/= Loan 600,000/= (b) What is the aim of preparing balance sheet 8.(a) The third, fifth and eighth terms of� arithmetic progression� A.P form the first three terms of Geometric Progression G.P . If the common difference of the A.P is 3, find (i)The first term of the G.P (ii)The sum of the first 9 terms of the G.P to one decimal place. (b)� Find the sum of first eight terms of the following sequence 1, -2, 4, -8 . . . . . � 9. (a) In the figure below� BD=5cm, DC=5cm and DE=3cm. Find length of AC and AE (b) A plane is flying at a constant height. The pilot observed of an angle of depression of 270 to one end of the lake and 150� to the opposite end of the lake. If� the lake is 12 km long. Determine the altitude of the plane. 10. (a) 10 years ago a man was 12 times as old as his son and 10 years from now a man will be twice as old as his son. Find their present age. (b) Find the values of x that satisfy the equation log(x+5) + log(x + 2) = log4 SECTION B ( 40 marks) Answer all questions from this section. 11. The examination scores in Basic Mathematics of 40 Form IV students are given in the following cumulative frequency table Class Interval 10-19 20-29 30-39 40-49 50-59 60-69 Cumulative Frequency 3 6 12 22 35 40 (a)Find the mean score using assumed mean A=44.5 (b)Draw Histogram and use it to estimate the mode (c)Calculate the median 12.(a) The two towns P and Q lie on the earths surface such that P(650N, 960E) and Q(650N, 840W). Find the distance between the towns in kilometers and nautical miles. (b) The figure below shows a tetrahedron. The length of each edge is 8cm. O is the centre of triangle ABC. Calculate (i)The length of VO (ii)The angle between line AV and the plane ABC (c) Find the volume of a cone which has a base diameter of 10 cm and slant height of 13 cm. 13. (a) The matrices� � are such that AB=A + B. Find the values of a, b, c and d (b)Triangle PQR vertices at P(2, 2), Q(5, 3) and R(4, 1) is mapped onto triangle PQR by transformation matrix� Find coordinate of triangle PQR (c)Determine the values of x which the matrix below has no inverse 14.(a)Given that h(x)= -1 - | x + 3| i.Sketch the graph of h(x) ii.Use the graph to deduce domain and range (b) The manager of a car park allows 10m2 of parking space for each car and 30m2 for each lorry. The total space available is 300m2. He decides that the maximum number of vehicles at any time must not exceed 20 and also insists that there must be at least as many cars as lorries. If the number of cars is X and the number of lorries is Y. (i) Write down the inequities which must be satisfied (ii)If the parking charge is sh.10 for each car and sh.50 for each lorry. How many vehicles of each kind he should admit to maximize his income and calculate his income �
�
 �
�![]() ���� and��������
���� and�������� ![]() ����
����![]() �
�![]()
![]() �
�
FORM FOUR MATHEMATICS EXAM SERIES 53
FORM FOUR MATHEMATICS EXAM SERIES 53
PRESIDENT�S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
041BASIC MATHEMATICS
(For Both School and Private Candidates)
Time:3 HoursWednesday, 5th August 2020 a.m.
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in section A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your examination number on every page of your answer booklet(s)
SECTION A (60 Marks)
Answer all questions in this section.
1. ![]()
![]()
![]()
![]()
![]()
2. ![]()
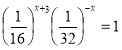
![]()
3. (a) A box contains 4 white balls and 5 black balls. Two balls are selected at random without replacement. Find the probability that
(i) Both are white balls
(ii) The first is black and the second is the white ball
(b) In a class of 15 students who take either Mathematics or Biology, 12 students take Mathematics, 8 students take Biology. If each student takes either subjects find by using formula the number of students who take Biology but not Mathematics.
4. (a) The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
(b) The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
5.(a) The area of the triangle ABC is 140 cm2, AB = 20, AC = 14cm, find the angle BAC
(b) Triangle XYZ is similar to triangle ABC and XY = 8 cm. If the area of the triangle XYZ is 24 cm2 and the area of the triangle ABC is 96 cm2. Calculate the length of AB.
6.![]()
![]()
![]()
![]()
![]()
7. ![]()
![]()
![]()
![]() =
=
![]() /=
/=
19 bought Shelves for cash 110,000/=
20 sold goods for cash 900,000/=
21 purchases goods for cash 800,000/=
22 sold goods for cash 1, 400,000/=
26 paid rent 300,000/=
Record the above transactions in Cash account ledger and extract a Trial balance.
8. (a). The product of a three terms of a geometric progression (GP) is 8000. If the first term is 4. Find the second term and third term
(b). Mahona invested a certain amount of money in a Savings Bank whose interest rate was 10% compounded annually. After two years he got 5000 shillings.
- How much did he invest at the start?
- How much did he receives as Interest at the end of two years.
9. (a) Find the value of
Sin (1500) cos (3150) Without using mathematical tables
Tan (3000)
(b) Calculate the angles of a triangle which has sides of lengths 4m, 5m and 7m
10.(a). Given that x2 �y2 = 27 and x + y = 9 find the value of xy
(b). Solve the equation 2x2 � 3x � 5 = 0 by completing the square.
SECTION B (40 Marks)
Answer all questions
11. (a) The number of workers absent in 52 working days is given in a cumulative frequency table below
| No.of absent | 0 � 4 | 5 � 9 | 10 � 14 | 15 � 19 | 20 � 24 | 25 - 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find (i) Percentage of workers who are absent at least for 20 days
(ii) Median
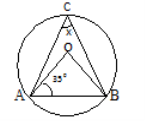
(b) Find the angle x in the figure below
12. (a) A ship sails from point A (40![]() ) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and
) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and ![]() (give your answer in nearest degree)
(give your answer in nearest degree)
(b) VABCD is a pyramid with VA=VB=VC=VD=5cm and ABCD is a square base of sides 4cm each. Assume that the centre of the base is at point N. Find
(i) The angle between VA and the base ABCD
(ii) The volume of the pyramid
13. ![]()
![]()
![]()
![]()
![]()
14. (a). A function F is defined by the formula f(x) = ![]() where x is a whole number
where x is a whole number
- If f(x) = 25 find the value of x
- Find the value of
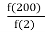
(b). A craftsman wishes to decide how many of each type A and B charcoal stove he has to fabricate in order to maximize profit for this month. Unit profit for type A stove is shs. 1000 and Unit profit for type B is shs. 1500. Type A stove requires 1m2 of mild steel sheet per unit and type B requires 2m2. He has only 12 m2 of mild steel available. He can fabricate a total of 8 stoves of either type per month. How many of each type should he fabricate?
FORM FOUR MATHEMATICS EXAM SERIES 45
FORM FOUR MATHEMATICS EXAM SERIES 45
Student’s Examination No.....................................
THE PRESIDENT’S OFFICE
MINISTRY OF EDUCATION, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
SECONDARY EXAMINATION SERIES
MATHEMATICS MID TERM EXAMINATION-MARCH
FORM FOUR-2021
Time: 3Hours
Instructions.
- This paper consists of section A, and B with a total of 14 questions
- Answer all questions in section A and B.
- Each question in Section A carries 06 marks, while each question in section B carry 10 marks
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables and non programmable calculators may be used.
- Cellular phones and any unauthorized materials are not allowed in the examination room.
- Write your number on every page of your answer booklet.
SECTION A (20 Marks)
Answer All questions in this section.
- (a) Write;
- 4.20098 into two decimal places
- 0.002758 into two significant figures
- 0.0497 rounding off to hundredth
(b) Use mathematical tables to evaluate ![]()
- (a) Solve for
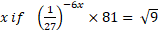
(b) Evaluate ![]() without using mathematical tables
without using mathematical tables
- (a) Two sets A and B are subsets of a given universal set µ =
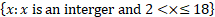 Find
Find
(b) A mother’s age is four times the age of her daughter. If the sum of their ages is 50 years, find the age of the mother.
- (a) Given that
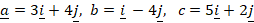
Find the magnitude of ![]()
Leaving your answer in the form of ![]()
(b) Find the equation of the line passing at the point (6,-2) and it is
perpendicular to the line crosses the ![]() – axis at 3 and the
– axis at 3 and the ![]() – axis at -4
– axis at -4
- (a) The ratio of the areas of two similar polygons is 144:225. If the length of a side of the small polygon is 60cm, find the length of the corresponding side of the other polygon.
(b) Find the length of a side and the perimeter of a regular nonagon inscribed in a circle of radius 6cm
- (a) The variable
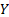 is directly proportional to
is directly proportional to 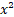 and inversely proportional to
and inversely proportional to 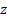 . If
. If 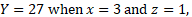 find
find 
(b) A car is travelling steadily covers a distance of 480km in 25 minutes. What is its rate in ![]()
- (a) a car was bought for 4,000,000/= and sold for 4,500,000. Calculate
- The profit made
- The percentage profit
(b) A factory employs skilled, semi-skilled and office workers in the ration 6:5:4 respectively. If there are 120 semi-skilled workers, how many skilled workers are there?
- (a) The sum of the first six terms of an A.P is 72 and the second term is seven times the fifth term. Find the sum of the first ten terms of this A.P
(b) Find the amount accumulated at the end of 2 years after investing 500,000/= at a compound interest rate of 10% annually.
- (a) Without using tables, evaluate
(b) a ladder reaches the top of a vertical wall 18m high when the other end on the ground is 8m from the wall. Find the length of the ladder correct to one decimal place
- (a) Solve the equation
 by using quadratic formula.
by using quadratic formula.
(b) Pulukuchu is 6 years younger than her brother Mpoki. If the product of their age is 135, find how old is Pulukuchu and Mpoki
SECTION B (40 MARKS)
- A small industry makes two types of clothes namely type A and type B. Each type A take 3 hours to produce and uses 6 meters of material and each type B take 6 hours to produce and uses 7 meters of material. The workers can work for a total of 60 hours and there is a 90 meters of materials available. If the profit on a type a cloth is 4,000 shillings and on type b Is 6,000 shillings, find how many each.
- The following distribution table shows the scores of 64 students in a chemistry weekly test;
| Scores | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Frequency | 5 | 10 | 15 | 17 | 4 | 6 | 7 |
- Calculate the mean and mode (do not us assumed mean)
- Draw the give and use it to estimate the median
- (a) Calculate the distance from Chagwe (5?S, 39?E) to Minga (12?S,39?E) in kilometres. Use π = 3.14, and th radius of the earth R = 6370 km and write the answer correct to 1 decimal place.
(b) If a bus leaves Chagwe at 8.00 am on Monday and travels at 40km/hour, at what time will it reach Minga?
(c) Find the values of ![]() in the figure below;
in the figure below;
- Study the following trial balance and then answer the questions that follow:
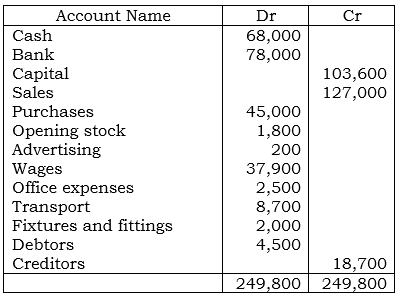
NB: Closing stock was Tshs 7,400;
Prepare:
- Trading profit and loss account
- Balance sheet
- (a) Find the inverse of matrix
A![]()
(b) Use the result of part (a) to solve the simultaneous equation;
![]()
(c) Find the value of ![]() which the matrix
which the matrix ![]() has no inverse
has no inverse
- (a) The function
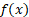 is defined by
is defined by
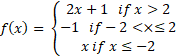
- Sketch the graph of
- State the domain and range of
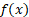
(b) The probability that Anna and John will be selected for advanced level is 0.5 and 0.3 respectively. Determine the probability that;
- Both of them will not be selected
- Anna will be selected and John will not be selected
- One of them will be selected
1 | Page
FORM FOUR MATHEMATICS EXAM SERIES 44
FORM FOUR MATHEMATICS EXAM SERIES 44
THE PRESIDENT'S OFFICE
MINISTRY OF REGIONAL GOVERNMENT AND LOCAL GOVERNMENT
PRE-NATIONAL EXAMINATION SERIES-1
MATHEMATICS FORM-4
2020
TIME: 3:00 HRS
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in sections A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) Mangoes are to be exactly divided into groups of 20, 30 or 36 .What is the minimum number of mangoes required?
(b) Mary was given 60,000 shillings by her mother. She spent 35 percent of the money to buy shoes and 10 percent of the remaining money to buy books. How much money remained?
2. (a). Evaluate log10 40,500 given that log10 2 = 0.3010 , log10 3 = 0.4771 and log10 5 = 0.6990.
(b). Find the values of x and y if
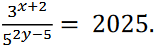
3(a) Factorize the following expressions:
(i) 16y2 +xy -15x2
(ii) 4 - (3x - 1)2
(b) At Moiva’s graduation ceremony 45 people drank Pepsi-Cola, 80 drank Coca-Cola and 35 drank both Pepsi-Cola and Coca-Cola. By using a Venn diagram, found out how many people were at the ceremony if each person drank Pepsi-Cola or Coca-Cola.
4. (a) Given vectors a = 6i + 12j, b = 17i + 18j :
(i) Find the vector c = 2a – b and its magnitude correctly to 3 significant figures. (ii) Represent vector c in part (a)(i) on the x - y plane.
(b) Find the equation of the line passing passing through the midpoint of the points A(− 3 2, ) and B(1,− )4 and which is perpendicular to line AB .
5. (a) In triangle ABC , X , Y and Z are the midpoints of sides AB , AC and BC respectively. If
ZX = ZY and ZXBˆ = ZY Cˆ = 90°;
(i) Represent this information diagrammatically, (ii) Show that ABZˆ = ACZˆ .
(b) The areas of two similar polygons are 27 and 48 square metres. If the length of one side of the smaller polygon is 4.5 cm, find the length of the corresponding side of the larger polygon.
6. (a) The variable v varies directly as the square of x and inversely as y. Find v when x = 5 and y = 2 ? given that when v = 18 and x = 3 the value of y = 4 .
(b) The temperature (Ti) inside a house is directly proportional to the temperature (To) outside the house and is inversely proportional to the thickness (t) of the house wall. If Ti = 32°C when To = 24°C and t = 9cm , find the value of t when Ti = 36°C and To = 18°C
7.(a)Given that 49, x and 81 are consecutive terms of a geometric progression. Find:
(i) The value of x.
(ii)The geometric mean.
(b) A wall is in the shape of a trapezium. The first level of wall is made-up of 50 bricks where as the top level has 14 bricks. If the levels differ from each other by 4 bricks, determine the number of
(i) levels of the bricks.
(ii) bricks used to make the wall.
8. (a) Three relatives shared Tshs 140,000 so that the first one got twice as much as the second, and the second got twice as much as the third. How much money did the first relative get?
(b) Kitwana paid Tshs 900,000 for a desktop computer and sold it the following year for Tshs 720,000. Find:
- The loss made,
- The percentage loss.
10. (a) Solve the equation 4x2 ? 32x + 12 = 0 by using the quadratic formula.
(b) Anna is 6 years younger than her brother Jerry. If the product of their ages is 135, find how old is Anna and Jerry.
9. (a) A river with parallel banks is 20 m wide. If P and Q are two points on either side of the river, as shown in the figure below, find the distance PQ.

(b) In the triangle LMN , LM = 5m, LN = 6m and angle MLN = 66°. Find MN .
SECTION B (40 Marks)
Answer four (4) questions from this section.
11. A shopkeeper sells refrigerators and washing machines. Each refrigerator takes up 1.8 m 2 of space and costs 500,000 2 of space and costs 300,000 shillings; whereas each washing machine takes up 1.5 mshillings. The owner of the shop has 6,000,000 shillings to spend and has 27 m 2 of space.
(a) Write down all the inequalities which represent the given information.
(b) If he makes a profit of 30,000 shillings on each refrigerator and 40,000 shillings on each washing machine, find how many refrigerators and washing machines he should sell for maximum profit.
12. (a) Given:
Opening stock 01-01-2012 34,430/=
Closing stock 31-12-2012 26,720/=
Net purchases during 2012 212,290/=
Expenses for the year 45,880/=
Gross Profit is 50% of cost of goods sold
Find: (i) Cost of goods sold (ii) The gross profit
(b) On 1 st June, 2013 Mrs. Lemisha started business with capital of 100,000/= and mad ehte following transactions
June 2 bought furniture 40,000/=
7 bought goods 70,000/=
11 sold goods 65,000/=
16 paid Sundry expenses 30,000/=
19 cash sales 80,000/=
24 paid wages 50,000/=
26 withdraw cash 30,000/=
(i) Prepare the cash account
(ii) Prepare the balance sheet as at 30/06/2013
(iii) Explain the importance of the balance sheet you have prepared in part (b)(ii) above.
13.(a) Given matrices
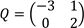
And
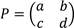
Such that
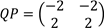
Find elements of matrix P
(b) Determine the matix A from the equation
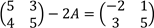
14.(a) A ship sails from Pemba (4.5°S, 39.5°E) to Dar es salaam (7.5°S, 39.5°E). If it leaves Pemba at 11:30 am and arrived in Dar es salaam at 13:30 pm, use  and RE=6370km to find speed of ship in km/h
and RE=6370km to find speed of ship in km/h
(b) Sketch a square pyramid whose base is PQRS, vertex is at W and centre is at N, then answer the questions that follow:
(i) State the projection of 
(ii) Name the angles between 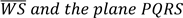
(c) The volume of a square pyramid is 28.2 cm3. If the sides of its base are 4 cm long, find the height of the pyramid correct to one decimal place.
FORM FOUR MATHEMATICS EXAM SERIES 28
FORM FOUR MATHEMATICS EXAM SERIES 28
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
MID TERM EXAMIATIONS
024 MATHS- FOUR
Duration: 3 Hours
INSTRUCTIONS.
- This paper consists of two sections A and B.
- Answer all questions in Section A and only four questions in section B
- Show clearly all working for each question
- Mathematical tables, geometrical instruments and graph paper may be used where necessary
SECTION A (60 MARKS)
1. a) Use mathematical table, evaluate
![]()
b)Express 45.456 in form of ![]() where a and b are both integers.
where a and b are both integers.
2. a) If ![]() ,
,
evaluate ![]()
b)Solve for x the following equation 32x-3 X 8x+4 = 64 ![]() 2x
2x
c)Rationalize the denominator ![]()
3. a) Find value of P which makes the following equations perfect square
i) x2 + 8x +P=0
ii) x2 - ![]() x + P=0
x + P=0
b) Solve for x the equation ![]()
4. a)Given the universal set U={p, q, r, s, t, x, y,z} A={p, q, r, t} B={r, s, t, y }. Find i)(AUB) ii)(A’nB’)
b)In a class of 60 students, 22 students study Physics only, 25 study Biology only and 5 students study neither Physics nor Biology. Find i) Number of students study Physics and Biology. ii) Number of students that study Biology.
5. a) A, B and C are to share T.sh 120,000/= in the ratio of![]() . How much will each get?
. How much will each get?
b)A radio is sold at T. sh 40,500/= this price is 20% value added tax(V.A.T). Calculate the amount of V.A.T.
6.a) The sum of 1st n-terms of certain series is 2n-1, show that this series is Geometric Progression. Find an the nth term of this series.
b) Point P is the mid-point of a line segment AB where A(-3,8) and B(5,-2), find an equation through P which is perpendicular to AB.
7.a) Without using mathematical table, evaluate ![]()
b) A man standing on top of cliff 100m high, is in line with two buoys whose angles of depression are 170 and 210. Calculate the distance between the buoys.
8.a) The lengths of two sides of triangle are 14cm and 16cm. Find the area of the triangle if the included angle is 300.
b)The area of a regular 6-sided plot of land inscribed in a circular track of radius r is 720cm2. Find the radius of the track.
9.a) Find values of angles marked x0 and y0 in the figure below
b) Prove that exterior angle of cyclic quadrilateral is equal to interior opposite angle.
10. a)Solve for x if ![]()
b) A two-digit of positive number is such that, the product of the digits is 8. When 18 is added to the number, then the digits are reversed. Find the number.
SECTION B (40 MARKS)
11. The daily wages of one hundred men are distributed as shown below
| Wages in T.Sh. x 1,000 | 3.0-3.4 | 3.5-3.9 | 4.0-4.4 | 4.5-4.9 | 5.0-5.4 | 5.5-5.9 | 6.0-6.4 | 6.5-6.9 |
| Number of men | 4 | 6 | 10 | 14 | x | 20 | 14 | 6 |
a) Find the value of x
b) Calculate the daily mean wage of the 100 men
c) Draw histogram to represent this data and use it to estimate Mode
d) Draw cumulative frequency curve and use it to represent Median
12. Shirima makes two types of shoes A and B. He takes 3hours to make one shoe of type A and 4hours to make one shoe of type B. He works for a maximum of 120hours. It costs him sh. 400 to make a pair of type A and sh. 150 to make of type B. His total cost does not exceed sh.9000. He must make at least 8 pairs of type A and more than 12 pairs of type B.
a) Write down the inequalities that representing the given information.
b) Represent these inequalities graphically
c)Shirima makes a profit of sh. 150 on each pair of type A and sh.250 on each pair of type B. Determine the maximum possible profit he makes.
13. The following trial balance was extracted from the books of Magoma Moto at 31stt December 2015
| Name Of Account | Dr | Cr |
| Sales | 1,800,000/= | |
| Purchases | 1,155,000/= | |
| Opening Stock | 377,000/= | |
| Carriage inwards | 32,000/= | |
| Carriage outwards | 23,000/= | |
| Return Inwards | 44,000/= | |
| Return Outwards | 35,000/= | |
| Salaries and wages | 244,000/= | |
| Motor expenses | 66,000/= | |
| Rent | 45,000/= | |
| Discount allowed | 12,000/= | |
| General office expenses | 120,000/= | |
| Motor vehicles | 2,400,000/= | |
| Furniture and Fittings | 600,000/= | |
| Debtors | 457,000/= | |
| Creditors | 304,000/= | |
| Discount Received | 35,600/= | |
| Cash at bank | 387,000/= | |
| Cash in hand | 12,000/= | |
| Drawings | 205,000/= | |
| Capital | 4,005,000/= |
Stock at 31stt December 2015 was Tsh.499,000/=
a) Prepare trading, profit and loss account for the year ended 31stt December 2015
b)The balance sheet as at 31stt December 2015
14.a) In the triangle ABC below, find values of angles marked x0 and
y0 where AB=12cm, BC=7cm and AC=8cm
b) Solve the following equations given that ![]()
i) ![]()
ii) ![]()
c) Show that ![]()
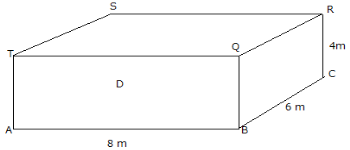
15. a) In a figure below, represents a room 8m by 6m by 4m. Calculate
i)Length of diagonal AR
ii) Angle that AR makes with the floor
iii) Angle which plane TSAD makes with plane TSBC.
b)A water pipe made of material 2cm thick has an external diameter of 16cm. Find the volume of material used in making of the pipe 200m long.
16. a) The function f is defined as follows:
F(x) = 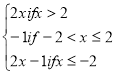
![]()
i) Sketch the graph of f(x)
ii) Determine domain and range
iii) Find i) f(1) ii) f(-4) iii) f(π)
b)For what values of x is function f(x)=![]() is undefined?
is undefined?
FORM FOUR MATHEMATICS EXAM SERIES 6
FORM FOUR MATHEMATICS EXAM SERIES 6
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256