FORM TWO MATHEMATICS EXAM SERIES 206
FORM TWO MATHEMATICS EXAM SERIES 206
FORM TWO TERMINAL EXAMINATION
BASIC MATHEMATICS
Time: 2:30 Hours Year : 2022
Instructions
1. This paper consists of ten (10) compulsory questions.
2. Show clearly all the working and answers in the space provided.
3. All writing must be in blue or black ink except drawings which must be in pencil.
4. NECTA mathematical tables, geometric instruments and graph papers may be used where necessary.
5. All communication devices, calculators and any unauthorized materials are not allowed in the assessment room.
6. Write your Assessment Number at the top right corner of every page.
1. (a) Calculate the sum of the GCF and LCM of 42, 45, 50.
(b)![]()
2.(a) Convert (i)256800cm into km
(ii)0.125 into percentage
(b) Round off (i) 260743 to the nearest thousand
(ii) 0.04261 to three decimal places
3.(a) Factorize the expression ![]()
(b)![]()
4. (a) Make A the subject of the formula ![]()
(b) If 4tanB=3 and B is an acute angle, find the value of;
- Cos B
- 4 tan B + sin B
(c) A straight line passes through two points A(-3, 6) and B (-6, 3). Find the gradient of the line AB
5. (a) Find (i) the largest possible number; and
(ii) The smallest possible number by changing order of the digits in 47986.
(b).Write 0.0.346 in standard form.
6. (a) In a certain office, every man owns either a car or a lorry or both 23 own lorries, 14 own cars and 5 own both lorries and cars. How many men are there in that office?
(b) .Joyce used 1/3 of her money to buy sugar, 1/4 of it to buy soap and she remained with Shs 35/=
- How much money did she have at the beginning?
- How much money did she use to buy sugar?
7. (a) Simplify ![]()
(b)Use a number line to find the sum of ![]()
(c)Arrange 2/5, 5/8, 48% and 0.6 in ascending order of magnitude.
(d)Decrease 160,000 by 16%
8. (a) Rationalize the denominator of ![]()
(b) Show on the number line the solution set of the inequality ![]()
9. (a)Without using Tables evaluate ![]()
(b)Given A=1/2 where A is an acute angle, find the value of 1 – cos2 A.
10. (a) Simplify ![]()
(b)If N=2x10-8 find the value of 1/N in scientific form
(c) Find the equation of a line through the point (2, -2) crossing the y-axis at the same point as the whose equation is ![]()
FORM TWO MATHEMATICS EXAM SERIES 106
FORM TWO MATHEMATICS EXAM SERIES 106
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM TWO BASIC MATHEMATICS TERMINAL EXAMINATION
Time: 2:30 Hours Year: 2022
Instructions
1.This paper consists of ten (10) compulsory questions.
2.Show clearly all the working and answers in the space provided.
3.All writing must be in blue or black ink except drawings which must be in pencil.
4.NECTA mathematical tables, geometric instruments and graph papers may be used where necessary.
5.All communication devices, calculators and any unauthorised materials are not allowed in the assessment room.
ATTEMPT ALL QUESTIONS
1. (a)(i)List down all the prime numbers between 1 and 12 and represent the numbers on the number line
(ii) Find the H.C.F and L.C.M of the numbers 8, 12 and 20 by prime factorization
(b)(i) Evaluate
![]()
(ii) Evaluate ![]()
(iii)Evaluate
![]()
(c)Evaluate
![]() .
.
Write your answer in repeating decimal notation
2. (a) The distance between two points is 30.567km. Write the distance in metres in one significant figure
(b) The velocity of a car between two stations AB and BC is 40m/sec and 60km/hr. respectively. Find the average velocity in m/minute assuming that AB and BC are straight roads
(c)If 6,000/= amount to 9,600/= in five years simple interact what is the percentage rate?
3. (a) Given that the rectangle ABCD is similar to rectangle MBCN below
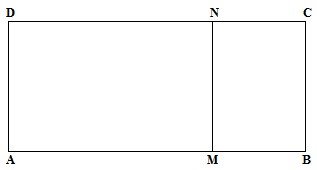 |
AB=10 BC=6 and
NC=x
(i )Find the value of x
(ii) Verify that the ratio of the areas = k2 where k is the ratio of the sides
(b)If ![]() is isosceles where AD=BD and E and C are the mid-points of AD and BD
is isosceles where AD=BD and E and C are the mid-points of AD and BD
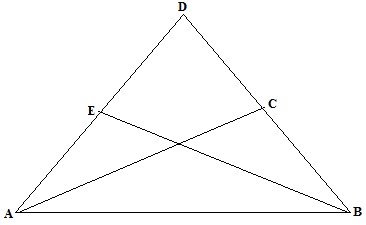
Prove that ![]() (congruent)
(congruent)
4. (a)Evaluate
i. ![]()
ii. ![]()
(b)Solve for x and y
i. ![]()
ii. If x=5 and y=3, Find the value of ![]() ,
,
(c) If ![]() , make p the subject
, make p the subject
5. (a)Find the value of
i. ![]()
ii. ![]()
(b)Find x
i. ![]()
ii. ![]()
(c)With the use of common logarithm find x
i. ![]()
ii. ![]()
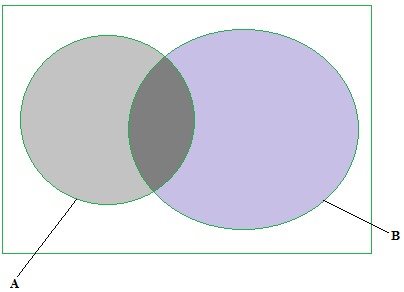
6. (a) A and B are two intersecting circles of radius 4cm and 6cm respectively. Find the area enclosed by A![]() B, is 10cm2, find the area enclosed by the circles (shaded)
B, is 10cm2, find the area enclosed by the circles (shaded)
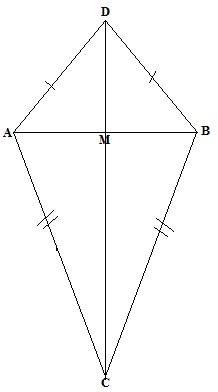
(b) In figure below, Triangles ABD and ABC are two isoscetes triangles CD=36cm, AB=12cm and ![]() Find the area of the figure ACBD
Find the area of the figure ACBD
(c)Find the area of squire whose length of the diagonal = 6cm
7. (a)Find the equation of the line perpendicular to the 2y – x – 6=0 and passing through the point (4,6)
(b) Represent the equation in (a) in forms
i. y=mx+c
ii. ![]() (A and B are x-intercept and y-intercept)
(A and B are x-intercept and y-intercept)
(c) The point A (4, 3) is reflected in the line y=x. What are the coordinates of the image?
8. (a)(i)Express; ![]() as a perfect squire
as a perfect squire
(ii) If (6+x)(8+x) = ![]() find the value of a and b
find the value of a and b
(b) Factorize.
i. ![]()
ii. ![]()
iii. ![]()
(c) Evaluate ![]()
9. (a) An item is sold at 480,000/= with profit of 20%
i. Find the ratio of the buying price to the selling price
ii. If the same item would be sold at 360,000/= what would be the percentage lose ?
(b)Find the interest for a principal of 100,000/= at 4% compound interest after 10years
(c)Tarimo wants to borrow 10 million Tanzania shillings from a Bank to promote his business. The Bank agree to charge his compound interact at 10% per year. How much interest Mr. Tarimo will owe the bank at the end of 5 years?
10. (a)Solve the equation: ![]() by
by
i. Factorization
ii. Completing the square (using the formula)
(b) Solve the following simultaneous equation
i. ![]()
ii. ![]()
(c)Solve the following inequalities
i. 3x + 6 < 10 – 5x
ii. ![]()
FORM TWO MATHEMATICS EXAM SERIES 105
FORM TWO MATHEMATICS EXAM SERIES 105
THE PRESIDENT’S OFFICE MINISTRY OF EDUCATION, LOCAL ADMINISTRATION AND LOCAL GOVERNMENT
MATHS- TERMINAL EXAMINATION-MAY
FORM TWO
Time 2:30 Hours MAY 2020
Instructions
- This paper consists of two sections A and B.
- Answer all questions in both sections
- Show clearly all working for each question
- Geometrical instruments and graph paper may be used where necessary
- Use
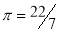
SECTION A (60 MARKS)
1. a) Rearrange the following in ascending order ![]()
b) Write 56 as the product of prime factors
2. Express ![]() in form of
in form of ![]() where p and q are both integers and
where p and q are both integers and ![]()
3. A room of length 270cm and 150cm is to be covered with square tiles. What is the largest size of the tiles to be used if no space of the room is left to be uncovered and how many tiles will be used?
4. Round off 34.9545 correct to i) Two significant figure ii) One decimal places
5. Write the following into 24-hours system i) 03: 15 Pm ii) 01: 01Pm
6. Given 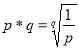 , find i) 64*3 ii) a if
, find i) 64*3 ii) a if ![]()
7. Two angles of pentagon are 580 and 380 and the other remaining three are in the ratio of 5:6:7. Find the largest angle.
8. Given a straight line 2y+5x+1=0, f
Fnd a) Slope b) y-intercept c) x-intercept
9. Two supplementary angles differ by 120. Find the angles.
10. Add the following
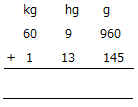
11. Anna is two years older than betty. Last year, Anna was two times as old as Betty. What is their age?
12. Make r-subject of formula in the following ![]()
13. Express ![]() in the form of
in the form of ![]()
14. Use method of difference of two squares to evaluate the following
i) ![]() ii) 0.9852 – 0.0152
ii) 0.9852 – 0.0152
15. Given log2=0.3010 and log7=0.8451, without using logarithm table evaluate:
a) log1.25 b) log 3.5
16. Factorize the following expression
a)15t2-14t-8=0 b) (2c+3)2 – c2
18.Simplifythe following
a)![]()
b) 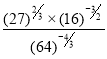
19. Expand the following
a) [y- 3] [ ![]() + y ] b) (6n -
+ y ] b) (6n - ![]() )2
)2
20. For value of P which makes the following equations perfect square
(i) x2 – Px +16=0
(ii) x2 - ![]() x + P=0
x + P=0
SECTION B (40 MARKS)
21. a) From the quadratic equation ![]() show that
show that 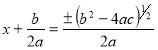
b) By using general formula of quadratic equation solve the following equation ![]()
22. The figure ABCD below is rectangle with sides as shown where C1 and C2 are two quarter circles inside it.
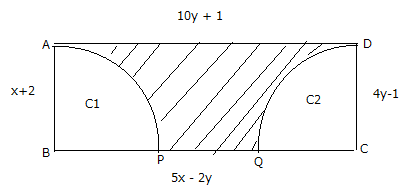
Find:
a) Value x and y shown in the figure
b) Perimeter of the rectangle
c)Area of the rectangle ABCD
d) Area of the shaded region
23.a) A rope is tired at the top of the flagpole and the other end of the rope is fixed on a point 36m from the base of the flagpole. If the flag pole is 15m high, what is the length of the rope?
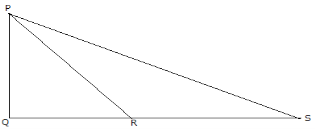
b) In the figure below find the length of PQ and PS if QR=8cm, RQ=12cm and PR=17cm.
24. A farmer sold a quarter of his maize harvest and give one third of the remaining to his relatives. If the farmer remained with 36 bags of maize, find:-
a) How many bags of maize did the farmer harvest.
b) How many bags of maize did the farmer sold.
25. a) By using logarithm tables, evaluate 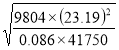
b) Evaluate the following without using logarithm tables:
(i) ![]()
(ii) 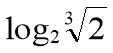
(iii) 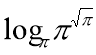
FORM TWO MATHEMATICS EXAM SERIES 14
FORM TWO MATHEMATICS EXAM SERIES 14
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256