CHAPTER 1: COORDINATE GEOMETRY
By the end of this chapter, you should be able to:
- Derive the general equation of a straight line.
- Determine the coordinates of mid-point of a line segment.
- Calculate the distance between two points on the xy-plane.
- Determine the conditions for both parallel and perpendicular lines.
- Solve problems involving parallel and perpendicular lines.
- Solve problems on parallel and perpendicular lines in real-life situation.
Equation of a Line
The General Equation of a Straight Line
Derive the general equation of a straight line
COORDINATES OF A POINT
•The coordinates of a points - are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.
The plane is called xy-plane and it has two axis.
- horizontal axis known as axis and
- vertical axis known as axis
Consider the xy-plane below
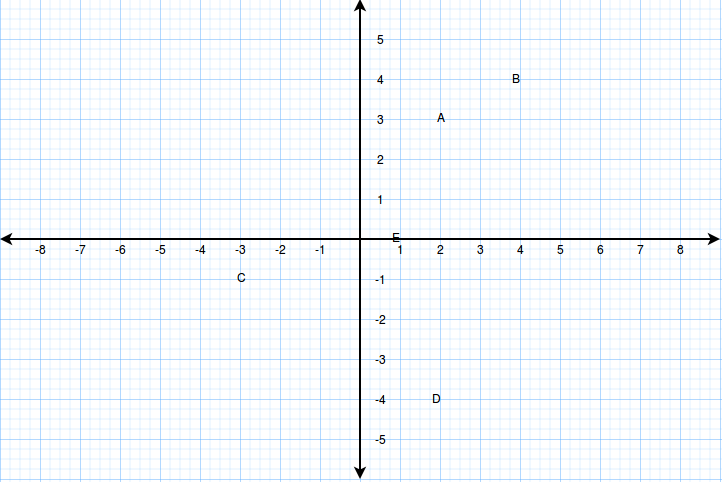
The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).
Definition

Example 1
Find the gradient of the lines joining
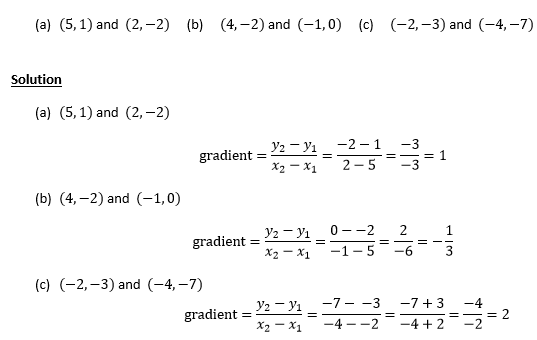
Example 2
(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

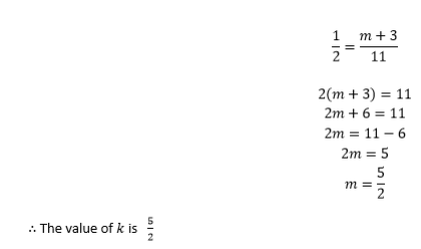
Exercise 1
1. Find the gradientof the line which passes through the following points ;
- (3,6) and (-2,8)
- (0,6) and (99,-12)
- (4,5)and (5,4)
2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?
3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.
FINDING THE EQUATION OF A STRAIGHT LINE
The equation of a straight line can be determined if one of the following is given:-
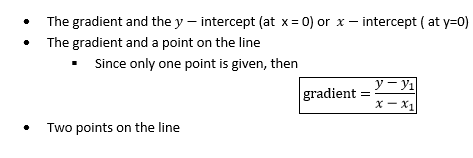
Example 3
Find the equation of the line with the following
- Gradient 2 and y-intercept -4
- Gradient -2/3 and passing through the point (2,4)
- A line passing through the point (3,4) and (4,5)
Solution


EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS
The equation of a line can be expressed in two forms

Example 4
Find the gradient of the following lines

INTERCEPTS

Therefore

Example 5
Find the y-intercept of the following lines

Example 6
Find the x and y-intercept of the following lines


Exercise 2
Attempt the following Questions.
- Find the y-intercept of the line 3x+2y = 18 .
- What is the x-intercept of the line passing through (3,3) and (-4,9)?
- Calculate the slope of the line given by the equation x-3y= 9
- Find the equation of the straight line with a slope -4 and passing through the point (0,0).
- Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).
GRAPHS OF STRAIGHT LINES
The graph of straight line can be drawn by using the following methods;
- By using intercepts
- By using the table of values
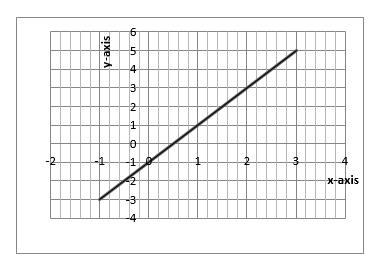
Example 7
Sketch the graph of Y = 2X - 1

SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD
- Use the intercepts to plot the straight lines of the simultaneous equations
- The point where the two lines cross each other is the solution to the simultaneous equations
Example 8
Solve the following simultaneous equations by graphical method

Exercise 3
1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point
2. Find the solutionfor each pair the following simultaneous equations by graphical method;
- y-x = 3 and 2x+y = 9
- 3x- 4y=-1 and x+y = 2
- x = 8 and 2x-3y = 10
Midpoint of a Line Segment
The Coordinates of the Midpoint of a Line Segment
Determine the coordinates of the midpoint of a line segment
Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:
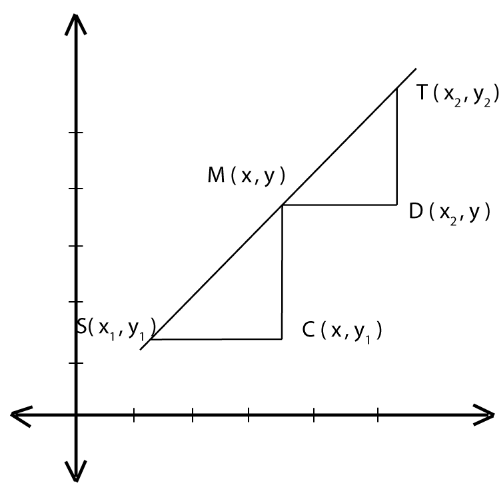 |
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9
Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)
Solution
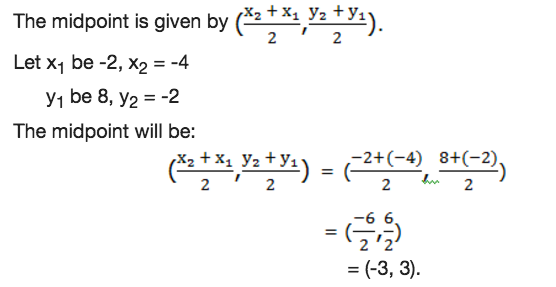
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).
Distance Between Two Points on a Plane
The Distance Between Two Points on a Plane
Calculate the distance between two points on a plane
Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:
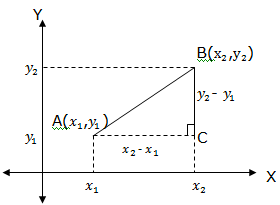
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.
Then, AC = x2– x1and BC = y2– y1
Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.
Parallel and Perpendicular Lines
Gradients in order to Determine the Conditions for any Two Lines to be Parallel
Compute gradients in order to determine the conditions for any two lines to be parallel
The two lines which never meet when produced infinitely are called parallel lines. See figure below:
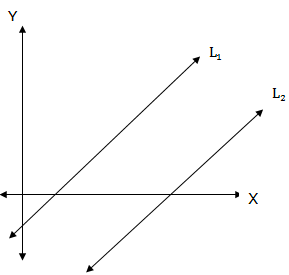
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2
Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular
Compute gradients in order to determine the conditions for any two lines to be perpendicular
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.
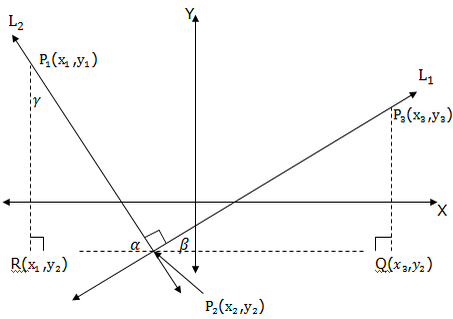
Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).
- α+β = 90 (complementary angles)
- α+γ= 90 (complementary angles)
- β = γ (alternate interior angles)
Therefore the triangle P2QP3is similar to triangle P1RP2.

Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.
Example 10
Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.
Solution
Let us find the slope of the lines AB, DC, AD and BC

We see that each two opposite sides of the parallelogram have equal slope. This means that the two opposite sides are parallel to each other, which is the distinctive feature of the parallelogram. Therefore the given vertices are the vertices of a parallelogram.
Problems on Parallel and Perpendicular Lines
Solve problems on parallel and perpendicular lines
Example 11
Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.
Solution
Right angled triangle has two sides that are perpendicular, they form 90°.We know that the slope of the line is given by: slope = change in y/change in x
Now,
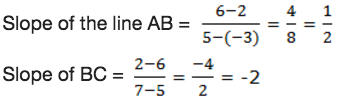
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.
Revision Question
1. Find the distance between point (? 3,? 2) and the point midway between (2,13) and (4,7). Write your answer in the form a?c where a and c are positive real numbers.
Soln.
Let (x, y) be the midpoint between
(2, 13) and (4,7)
![]()
![]()
The midpoint is (3, 10)
Let d be distance between (3,10) and (-3,-2)
d=![]()
d=![]()
d=![]()
d=![]()
d=![]()
d=![]()
Distance = ![]()
2. Find the equation of the line through the points (4,6) and the midpoint of (2,4) and (10,4).Soln.
Given points (4,6), (2,4) and (10,4)
Mid-point (x,y)![]()
![]()
Then new points are (4,6) and 6,4)
Slope = ![]()
Equation, y=m(x – x1)+y. Take point P(4,6)
y=m(x – x1) + y1
y=-1(x – 4)+6
y=-x+10
The equation of line y=-x+10
3. Find the equation of the line passing through (6,4) and perpendicular to the line whose equation is 12x + 6y = 9.
Soln.
If line L1 with slope M1 is perpendicular to line L2 of slope M2 then, M1 M2=-1
Let the equation of line L1 be: 12x + 6y=9 (given). Rearranging in the form y=mx + c,
6y=12x+9
![]()
![]()
M1M2=-2M2=-1
M2=![]()
Using the given coordinates,
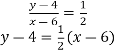
![]()
![]() is the required equation.
is the required equation.
4. The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
solution.
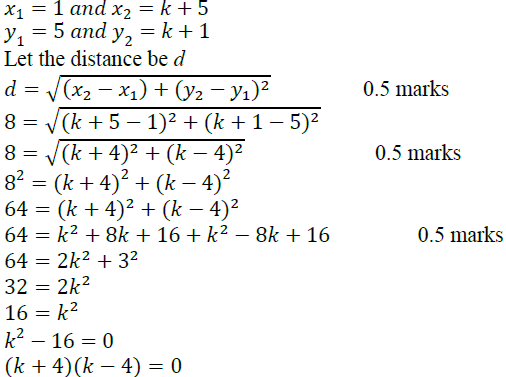
Therefore k =4 since k is positive. 0.5 marks.
5. The gradient of line L1is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
Soln.
let M1be the gradient of L1, M1 = −2let M2be the gradient of L2,
![]() 0.5 marks
0.5 marks
but M1M2 = -1 For perpendicular lines
-![]() 0.5 marks
0.5 marks
-2y − 4 = −x − 3
−2y = −x − 3 + 4 0.5 marks
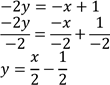
The equation is ![]() 0.5 marks
0.5 marks
6(a) The coordinate of P, Q and R are (2, m), (-3, 1) and (6, n) respectively. If the length of PQ is ![]() units and midpoint of QR is
units and midpoint of QR is ![]() find the possible value of m and n (b)The gradient of line
find the possible value of m and n (b)The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
Soln.
(a) Length of PQ=![]() …………………….00
…………………….00![]()
![]()
PQ=![]()
5![]() =
=![]()
![]() =
=![]() ………………………..00
………………………..00![]()
25x2= 25+![]()
50 = 25 +![]()
50-25 =1-2m+m2
25 = 1-2m+m2
M2-2m-24=0
M2+4m-6m+24= 0
M(m+4)-6(m+4)=0
(m-6)(m+4)=0
m-6=0 or m+4=0
![]() ………………………..01
………………………..01
Mid point of QR
From m(x,y) =![]() ………………………00.
………………………00.![]()
![]() =
=![]()
-1 = ![]() ……………………00
……………………00![]()
-2 = 1+n
![]() ……………00
……………00![]()
(b) Let m be the gradient of L1
m1= -2
Let m2 be the gradient of L2
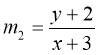 ..........................00 ½
..........................00 ½
![]() ...............................00 ½
...............................00 ½
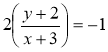 ........................................................ 00 ½
........................................................ 00 ½
![]()
![]()

The equation of L2 is 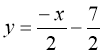 .................................00 ½
.................................00 ½
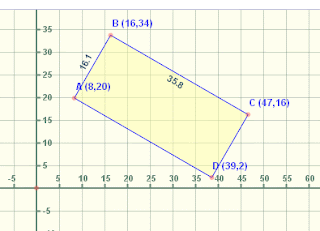
7. OBCA form a quadrilateral with coordinates A (-5, 0), B(4,3) C(-1,3) and O(0,0)
- Find the slopes of the line segments
- AO and CB (ii) AC and OB
- Find the distance AO, CB, AC and OB
- Find the equation of the lines AB and CO and show that they are perpendicular. Using name (a), (b) and (c) suggest the name of the quadrilateral OBCA
Soln. The coordinates of the quadrilateral OBCA are O(0,0), A(-5,0), C(-1,3) and B(4,3)
(i) Slopes AO=(-5-0)/(0-0)=0
Slope of CB = ![]()
AO and CB are parallel
(ii) Slope of AC and OB
Slope of AC= ![]()
Slope of OB = ![]()
OB and AC are parallel
(b)Distances
AO=![]()
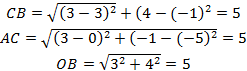
AO=CB=AC=OB
All the sides are equal in length
(c)Equation of AB
Slope of AB= ![]()
Equation of line AB
![]()
Equation of CO
Slope =![]()
Equation of line
![]()
Equation of CO:![]()
The lines AB and CO are perpendicular
Since, all the sides are equal and opposite sides are parallel, the quadrilateral OBCA is a rhombus.
8 An engineer is in the process of constructing two straight roads, RI and R, which will meet at the right angles. If RI will be represented by the equation 2x—3y—4=0 and R, will pass through the point , find the equation representing R2 in the form ax+by+c=0
Ans
Soln
Consider the figure below
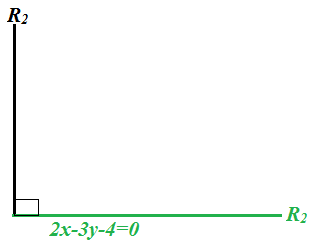
The equation of R1?2x – 3y – 4=0
2x – 3y – 4=0
3y=2x – 4
![]()
hence slope (m)=2/3
Since the two line are in perpendicular
m1m2 = -1
(2/3)m2=-1
![]()
But R2 pass through point (4, -2)
![]()
![]()
Cross-multiplication
![]()
![]()
![]()
![]()
![]()
9 Find the length of a line segment joining the points (3,-2) and (15,3) .
Soln.
![]()
![]()
![]()
![]()
L=13 unit length.
10 Let P and Q be two points at (2,5) and (4, -1) respectively. Find
(i)Find equation of the line that passes through the midpoint of PQ and is perpendicular to it in form of ax + by +c=0
(ii)The distance between P and Q
Soln.
Given P(2,5) and Q(4, -1)
Slope of PQ
![]()
![]()
Form perpendicular line, M1M2 = -1
-3 x M2 =-1
M2 = 1/3
Now, midpoint of line PQ
![]()
![]()
M.P=(3 , 2)
![]()
x - 3 = 3y - 6
x - 3y + 3 =0
11 Find the equation of the line passing at point (6, 2) and it is perpendicular to the line that crosses the x-axis at 3 and the y-axis at 4.
Soln.
Given that; point (6, -2) is perpendicular to line that passes at point (3,0) and (0,-4)
Now, lets find slope(M1) of line athe passes at the two points
![]()
But for perpendicular lines, M1M2=-1
(4/3 ) M2=-1
So, M2=(-3/4)
![]()
Cross-multiplication above
-3(x - 6)=4(y + 2)
-3x +18= 4y +8
3x +4y +8 -18=0
Therefore, Equation Of A Line Is 3x +4y - 10=0
12 Find the equation of the line passing passing through the midpoint of the points A(? 3 2, ) and B(1,? )4 and which is perpendicular to line AB .
Soln.
Lets find the midpoint of A(? 3 2, ) and B(1,? 4)
From midpoint formula
![]()
![]()
M(x,y)=(-1, -1)
Now lets find the slope of line AB
![]()
But for perpendicula lines
M1M2 =-1
M2=-1/ M1 = -1 ÷ -3/2
M2=2/3
Now Eqn. of line
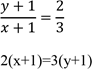
2x+2=3y+3
2x-3y=3-2
2x -3y=1
Therefore, Eqn. of a line is 2x -3y=1
13 . Find the point of intersection of the lines x ? 2y = ?5 and 2x + 7y ? 34 = 0
Soln.
Point of intersection btn line x ? 2y = ?5 and 2x + 7y ? 34 = 0 can be obtained by solve simultaneous equation
2x+7y=34 ...(i) Eqn 1
x-2y=-5
x=2y-5
Substitute x in the eqn1 that 2x+7y=34
2(2y-5) +7y=34
4y-10 + 7y=34
11y=34+10=44
11y=44
y=4
but x=2y-5
x=2x4 -5=8-5=3
x=3
Therefore, point of intersection is (3, 4)
14 The points P, Q and R are (5, —3), (-6, I) and (1, 8) respectively. Show that these points form an isosceles triangle.
soln.
Given point P, Q and R are (5,-3) (-6,1) and (1,8) respectivelly
Required to show these points form an is isosceles triangle.(Two sides are equal) Consider the triangle below:
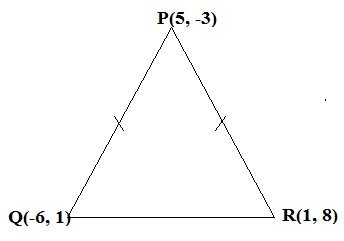
So, if is an isosceles triangle; PQ=PR
Recall distance formula
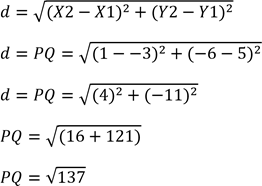
Now, find Length of PR
![]()
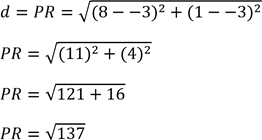
Since, PQ=PR, Hence triangle formed by points P, Q, R is an Isosceles triangle.
15 Find the equation of a line which passes through the point A(-3, 4) and which is parallel to the line 3x + 4y - 15=0.
soln
Condition for parallel line M1=M2
3x+4y-15=0
![]()
from eqn y= mx +c then, M1=-3/4
Therefore, M2= -3/4
Equation of line passes though point A(-3,4)
![]()
Now, cross multiplication
4(y-4) = -3(x+3)
4y-16 = -3x-9
4y+3x=-9+16
4y+3x=7
4y+3x-7=0
.:The equation of the line is 4y+ 3x-7=0
16 Show that triangle ABC is right-angled where A = (-2,-1), B = (2,1) and C = (1,3).
Soln.
Given, the vertices Of Triangle ABC are A(-2, -1), B(2, 1) and C(1, 3)
For triangle ABC to be right angled triangle, two lines must meet perpendicularly
For perpendicular lines: M1M2=-1
Slope of AB(M1)
![]()
M1= 1/ 2
Slope Of BC(M2)
![]()
M2=-2
M1 x M2= 1/ 2 x -2 =-1;
Therefore, triangle ABC is right-angled triangle.
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
WHATSAPP US NOW FOR ANY QUERY
App Ya Learning Hub Tanzania