APPLICATION OF VECTOR
At the end of this Topic you should be able to:
a) Distinguish between scalar and vector quantities
b) Add vectors using graphical methods
c) State the triangular and parallelogram law of forces
d)Explain the concept of relative motion
e) Calculate relative motion of bodies
f) Apply the concept of relative motion in daily life
KEY TERMS AND CONCEPTS.
- Scalar quantity- this is quantity that that has only magnitude
- Vector quantity – is a quantity with both magnitude and direction
- Resultant vector- this is the vector obtained when two vectors are connected by a third line.
- Triangle law of addition- It states that; "If three forces are in equilibrium and that two of the forces are represented in magnitude and direction by two sides of a triangle, then the third side of the triangle represents the resultant of the two forces"
- Parallelogram law of addition states; "If two forces/vectors are represented by the two sides given and they include angle
between them, then resultant of the two forces/vectors will be represented by the diagonal from their common point of a parallelogram formed by the two forces/vectors" - Relative velocity- This is the velocity of a body in relation to another
Scalar quantity.
Is a physical quantity with both magnitude only.
Examples are time, speed,distance,temperature, energy,mass, area, volume, density, volume, electric current etc.
Vector Quantities
Vector quantity is the any physical quantity that has both magnitude and direction.
Example, force, displacement, velocity, momentum, acceleration, etc
Vector Arithmetic
Scalar quantity can be added, multiplied, divided or subtracted.
Example, if you have two liquid in different measuring cylinder let say fist one contain 10 cm3 and second contain 20cm3 if you asked to find total volume you must add to obtain total volume
Vector quantity can be represented on a diagram by a directed line segment, consider the diagram below.
![]() a
a
The length of line segment represents the magnitude and the arrow represents the direction
NB:
- The direction can be represented by using compass direction
- Two vector are equal if the magnitude and direction the same.
When adding two or more vectors, by mathematical formula is used to sum up vectors. For example, pythogoras theorem, and trigonometric ratios.
- The triangle method and parallelogram method are used to adding two vectors.
- The vector we get after the adding of two or more vectors is called resultant vector
- Resultant vector can be added by mathematical or graphical/drawing
- Resultant vector is measured as an anticlockwise angle of rotation from due east
Adding By graphical Method
The following are steps followed when adding two or more vectors by graphical method
Choose a suitable scale and write it down on a graph paper
Pick starting and draw the first vector to scale direction stated (indicate the magnitude and direction)
Starting from the head of the first vector, draw the second vector to scale in the started direction until all given vectors finished
Draw the line to connect tail of the first drawn vector and the head of the last vector. This is called resultant vector
Measure the length of the resultant vector and convert to actual unit
Determine the direction of vector
Example,
Suppose a man walks starting from point A, a distance of 20m due north and then walks 15m due east. Find his new position from A
Solution
- Using a scale of 1 cm to represent 5 m
- Draw a vector AB 4cm due north.
- From B draw BD 3cm due east.
- Join A and D point
The resultant diagram is a triangle as shown below
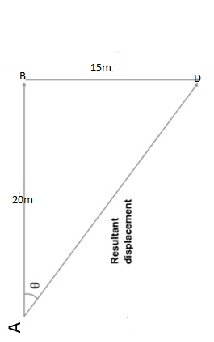
- Measure the length of AD
AD = 5 cm
Change to actual unit
lcm = 5 m
5 cm = ?
Cross multiplication you get 25 m
- Determine the direction of vector
Tanθ =![]() = 0.75
= 0.75
θ= 36051
Therefore position of D is represented by vector AD of magnitude 25 m at an angle of 36051 east of north
The Triangle Method/Triangle Law
The triangle law is appropriate when adding two vector quantities. The law state that
"If three forces are in equilibrium and that two of the forces are represented in
magnitude and direction by two sides of a triangle, then the third side of the triangle represents the resultant of the two forces"
Example,
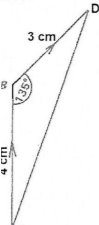
A brick is pulled by a force of 4N acting northward and another force of 3N acting north-east. Find the resultant of these two forces.
Solution
Data
Initial force, F1=4N northward
Final force, F2=3N north-east
Steps
i/ Using a scale of lcm to represent 1 N
ii/ Draw a vector AB 4cm due north.
iii/ From B draw BD 3cm at 450
iv/Join A and D point
The resultant diagram is a triangle as shown below
![]()
![]()
v/ Measure the length of AD
AD = 6.5 cm
Change to actual unit
lcm = 1 N
6.5 cm = ?
Cross multiplication you get 6.5 N
Therefore the resultant of these two forces= 6.5 N
Example,
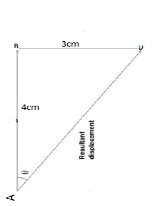
Two forces, one 8 N and the other 6 N, are acting on a body. Given that the two
forces are acting perpendicularly to eachother, find the magnitude of the third force which would just counter the two forces.
Solution
Data
Force, F1=8N
Force, F2=6N
Stapes
i/ Using a scale of 1 cm to represent 2 N
ii/ Draw a vector AB 4cm due north.
iii/ From B draw BC 3cm at 900
iv/Join A and C point
The resultant diagram is a triangle as shown below
v/ Measure the length of AC
AD = 5 cm
Change to actual unit
lcm = 2 N
5 cm = ?
Cross multiplication you get 10 N
Therefore magnitude of third force is 10 N
Parallelogram Method
The parallelogram law of vector is applicable when adding two vector quantities. The law state that
"If two forces/vectors are represented by the two sides given and they include angle
between them, then resultant of the two forces/vectors will be represented by the diagonal from their common point of a parallelogram formed by the two forces/vectors"
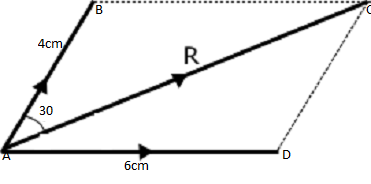
Example1;
Two forces AB and AD of magnitude 40 N and 60 N respective are pulling a body on horizontal table. If the two forces makes an angle 300 between them, find the resultant force on the, body.
Solution
Data
Force AB, FAB=40N
Force AD, FAD=60N
Angle between, θ=300
i/ Using a scale of 1 cm to represent 10 N
ii/ Draw a vector AD 6 cm horizontal from point A
iii/ From point A draw AB 3 cm at 300 from vector AD
iii/Complete the parallelogram ABCD
iv/ Join A and c point
The resultant diagram is a triangle as shown below
v/Measure the length of Ac
Ac = 9.7 cm
Change to actual unit
1 cm = 10 N
9.7 cm = ?
Cross multiplication you get 97 N
Therefore the resultant of these two forces 6.5 N
Example 2;
Two ropes of 3 m and 6 m long are tied to a ceiling and their free ends are pulled by a force of 100 N as shown in the figure below. Find the tensions in each rope if they make angle 30° between them.
Diagram:
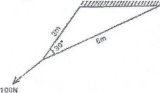
Data
Legth, l1=3m
Length, l2=6m
Force, F=100N
Angle between, θ=300
Solution
Steps
i/ Using a scale of 1 cm to represent 1 m
iii/ Draw a vector AD 6 cm horizontal from point A
iii/ From point A draw AB 3 cm at 300 from vector AD
iv/Complete the parallelogram ABCD
v/ Join A and c point
The resultant diagram is a triangle as
shown below

A 6 cm
vi/Measure the length of Ac
AC = 8.7 cm
AC is the equal to 100 N because action is equal to opposite reaction,
AC = 8.7cm =100 N
Now:
Tension at 3 cm calculated by:
8.7 cm = 100 N
3 cm = ?
Cross multiplication you get 34.5 N
Therefore the Tension at 3 cm is 34.50N
Then:
Tension at 6 cm calculated by:
8.7 cm = 100 N
6 cm = ?
Cross multiplication you get 69 N
Therefore the Tension at 6 cm is 69 N
Example,
Find the resultant force when two forces act as shown in the figure below.
![]() 6N
6N
![]() 8N
8N
Solution
Joining to line to get resultant force
 8N D
8N D
i/ Using a scale of 1 cm to represent 1 N
ii/ Draw a vector AD 8 cm horizontal from point A
iii/ From point A draw AB 6 cm at 900 from vector AD
iv/Complete the parallelogram ABCD V/ Measure the length of Ac
Ac = 10 cm
Change to actual unit
1cm = 1N
10cm = ?
Cross multiplication you get 10N
Therefore the resultant of these two forces 10N
Example,
Find the resultant force, F, when two forces,
9N and 15N, act on an object with an angle of 600 between them.
Solution
i/Using a scale of 1cm to represent 3N
ii/Draw a vector AD 5cm horizontal from point A
iii/ From point A draw AB 3cm at 600 from vector AD
iv/Complete the parallelogram ABCD
v/ Join A and c point
The resultant diagram is a triangle as
shown below
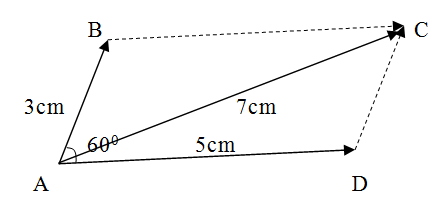
v/Measure the length of AC
AC = 7 cm
Change to actual unit
lcm = 3 N 7 cm = ?
Cross multiplication you get 21 N
Therefore the resultant force, F is 21 N
Relative Velocity
Relative velocity is the velocity of a body which observed by another moving or stationary body.
Or
Relative velocity is the velocity of a body with relative to the moving observer.
Nb:
- Velocity of one object let say VA respect another object let say VB is denoted by symbol VAB.
- if all object moving to the same direction, it seems to observe low speed, therefore we minus two velocity of moving body, (_VB)
VAB = VA + (_VB)
VAB = VA – VB
- if all object moving to the opposite direction, it seems to observe high speed, therefore we plus two velocity of moving body, (+VB)
VAB = VA + (+VB)
VAB = VA + VB
Relative velocity also can be calculated by triangle method and by parallelogram methods.
Example,
A plane travelling at a velocity of 100 km/h to the South encounters a side wind blowing at 25 km/h to the West. What is its velocity relative to an observer on the ground?
Data
Velocity of plane, Vp= 100km/h south
Velocity of plane, Vw= 25km/h west
Solution:
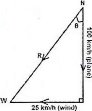
By using Pythagoras theorem,
R2= 252 + 1002
R2 = 625 + 10000
R2= 10625
R= ![]()
R = 103.1 km/h
Direction of resultant
Cos θ =![]()
Cos θ = ![]()
Cos θ = 0.9699
θ= 140 - clockwise to the east with the southward direction.
Since: Resultant vector is measured as an anticlockwise angle of rotation from due east
θ = 270° - 140- anticlockwise to the east θ = 256°
Example,
Car A is moving with a velocity of 20 m/s while car B is moving with a velocity of 30 m/s.
Calculate the velocity of car B relative to car A if:
{a} they are moving in the same direction
{b} They are moving in the opposite directions.
Data given
Velocity of Car A, VA = 20 m/s
Velocity of Car B, VB = 30 m/s
Relative velocity, VBA = ?
Solution:
{a} they are moving in the same direction
From: VBA = VB -VA
VBA =30 - 20
VBA = 10 m/s
{b} They are moving in the opposite directions.
From: VBA = VB + VA
VBA = 30 + 20
VBA = 50 m/s
Resolution of the Vector
As we study at trigonometrically ratio when we have values of hypotenuse and angle formed with horizontal we can calculate vertical component and horizontal component.
Consider the diagram below where the toy car pulls at a certain angle but it seems to move horizontally due to horizontal force/vector, not only that but vertical force/vector are formed
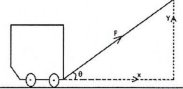
From the diagram:
Horizontal force/vector = x
Vertical force/vector = y
Extract the triangle from the above diagram
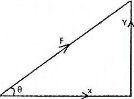
Horizontal force/vector is given by the formula
From:
cos θ = ![]() multiply by F both sides you get
multiply by F both sides you get
x = Fcos θ
Vertical force/vector is given by the formula
From:
Sin θ = ![]() multiply for F both sides you get
multiply for F both sides you get
y= Fsin 8
Example,
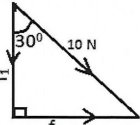
A nail is being pulled using a string from a wall. The string forms an angle of 30° with the normal. If the force being used is 10 N, part of the force will tend to bend the nail while the other part will try to pull it out.
Figure:
{a} Tend to bend the nails?
{b} Tend to pull the nails out?
Data
Force applied, F=10N
Angle made, θ=300
Solution:
Change the information above into vector form
F2
{a} Force tends to bend the nails, F1 = ?
F1 = 10 x cos 300
= 10 x 0.866
F1 = 8.66 N
{b} Force tends to pull the nails out, F2= ?
F2 = 10 x sin 300
F2= 10x0.5
F2 = 5.0 N
![]() Example,
Example,
A body is being acted on by two forces: F1 = 18N acting at an angle of 25° and F2 = 30 N acting at 140° from due East. Find the resultant of the two forces, F, by separating the forces into x- and y-components.
Solution:
Draw the diagram first
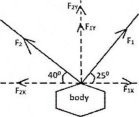
First find F1x and F2x
Where: F1= 18N F2 = 30 N From: X = F. Cos 0
F1x = F1 Cos 25
F1x = 18 x Cos 25
F1x = 18 x 0.9063
F1x = 16.31N - toward east
F2x = 22.98 N - toward west θ=76.06° - to the west or θ=103.94°- to the east
Assume the wanted direction is east so the an direction of force to west will be negative.
Find their net force, Fx = ?
Fx = F1x + F2X
Fx = 16.31 + (-22.98)
Fx = 16.31 - 22.98
Fx = - 6.67N - toward west
Second find Fly and F2y
Where:
F1= 1=18 N F2 = 30 N
From: y= F. Sinθ
Fly .= F1. Sin 25
Fly = 18 x Sin 25
Fly = 18 x 0.4226
Fly = 7.6N - toward north
Then:
F2y = F1. Sin 40
F2y = 30 x Sin 40
F2y = 30 x 0.6428
F2y = 19.28 N - toward north
Assume the wanted direction is north.
Find their net force, Fy = ?
Fy = Fly +F2y
Fy = 7.6 + 19.28
Fy=26.88N toward north
Modify the vector diagram
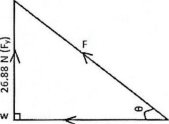
6.67 N (Fx)
Lastly find the resultant of the two forces, F =2
By using Pythagoras theorem,
R2= 26.882 + (-6.672)
R = 27.70 N
Get the direction tanθ = Fy/Fx
tanθ=26.88/6.67
tan θ = 4.03
θ= 76.060- to te west or θ= 103.94 to east
Therefore the resultant force is 27.70N at an angle of 103.94 to west.
SUMMARY
- Quantities can be represented as a vector or scalars. Vectors have both magnitude and direction while scalars have magnitude only.
- A vector quantity is represented quantity is represented graphically using a vector diagram. In a vector diagram, an arrow drawn to scale in a specific direction is to represent the vector.
- A resultant vector that is net effect of two or more vectors.
- The triangle law of vector addition states that if two vectors addition states that if two vectors are vectors are represented by two sides of a triangle in sequence, that if two sides of a triangle in sequence, then the third closing side of the triangle drawn from the tail of the first vector to the head of the two vector, represents the resultant of the two vectors in both magnitude and direction.
- The parallelogram law of vector addition states that: if two vectors are represented by two adjacent sides of a parallelogram, then the diagonal of the parallelogram through the common point represents the sum of the two vectors in both magnitude and direction.
- A two dimensional vector can be separated into two perpendicular vectors which are its components.
- Relative velocity of a body with respect to another moving body.
- We use the Pythagoras theorem , c2 ═ a2 ┼ b2, to find the result vector of two perpendicular vectors of two perpendicular vectors.
- A vector F has a component F cos o in a direction at angle o to itself and a component F Sin o in the perpendicular direct direction.
SAMPLE NECTA QUESTIONS
(a) State the parallelogram law of forces.
(b)(i) Distinguish between absolute velocity and relative velocity.
(ii) Wind is blowing 30° west of north at 20 km/hour. A bird is flying in the wind and its velocity relative to the ground is 90 km/hour at 75° west of north. Calculate the velocity and direction of the bird.
(c) (i) Define the coefficient of dynamic friction.
(ii) A body of mass 40 kg is placed in a straight track sloping at an angle of 45° to the horizontal. If the body is held from slipping by friction, calculate the normal reaction and the force of friction.
(a) State the parallelogram law of forces.
(b) (i) Distinguish between, Absolute velocity and relative velocity.
(ii) Wind is blowing west of north at 20km/hour. A bird is flying in the wind and its velocity relative to the ground is 90km/h at west of north. Calculate the velocity and direction of the bird.
(c) (i) Define, coefficient of dynamic friction.
(ii) A body of mass 40kg is placed in a straight track sloping at an angle to the horizontal . If the body is held from slipping by friction, calculate the normal reaction and the force of friction.
www.learninghubtz.co.tz
PHYSICS FORM THREE: TOPICAL EXAM.
APPLICATION OF VECTORS:
SECTION A:
MULTIPLE CHOICE QUESTIONS.
1. Choose the most correct answer.
(i) Identify the odd one out
- Force
- Displacement.
- Speed
- Velocity.
(ii) The vector we get after addition of two or more vectors is called?
- Head to tail vector
- Resultant vector
- Resultant force
- Vector addition
(iii) Two forces 9N and 15N act on an object with an angle of 60![]() between them; the resultant force will be?
between them; the resultant force will be?
- 15 N
- 20 N
- 21 N
- 10 N
(iv) Two forces one 8 N and the other 6N are acting on a body. Given the two forces are acting perpendicular to each other, find the magnitude of the third force which would just counter the two forces.
- 16 N.
- 8 N
- 10 N
- 2 N.
(v) Using the parallelogram law, find the resultant force when two forces 20N and 40N, are acting on an object with an angle of 45![]() between them.
between them.
- 56N
- 10.6N
- 60N.
- 20N.
(vi) Movement of an object as seen by an observer in anther object is called?
- Resultant force
- Relative velocity
- Relative motion
- Constant motion.
(vii) The influence of a vector to a given direction is called?
- Combined vector
- Coordinate vector
- Component vector
- Sum of vector
(viii) Two forces 4N and 6N are acting at an angle of 45![]() to one another. What is the resultant force?
to one another. What is the resultant force?
- 9.2N.
- 4.2N.
- 42N
- 0.42N.
(ix) If two vectors represented by two sides of a triangle in sequence then the third closing side of triangle drawn from tail of the first vector to head of second vector represent the resultant of the vectors in both magnitude and direction. This is?
- Parallelogram law.
- Resultant vector
- Triangle law
- Relative motion.
(x) The diagram below shows a block being pushed along a track. If a force of 20N is applied in direction A at an angle of 60![]() the resolved part of force in direction B will be.
the resolved part of force in direction B will be.
A. 10N
B. 20N
C. 12N
D. 17.32N
2. Match the items from list A with those in list B.
| LIST A | LIST B |
| (i) Has magnitude and direction (ii) Has magnitude only. (iii) Two vectors represented by two sides of triangle in sequence, then the third closing side of the triangle drawn from tall of the first vector to head of second vector represents the resultant of two vectors in magnitude and direction. (iv) Movement of object as seen by an observer in another object. (v) Velocity of a body in relative to another moving or stationery object. (vi) Four regions formed by two axes in a plane. (vii) Influence of a vector in a given direction. (viii) When two vectors are added up. (ix) Two vectors represented by two adjacent sides of parallelogram, then the diagonal of the parallelogram through the common point represent the sum of two vectors in both magnitude and direction. (x) Adding two vectors by placing the tail of 2nd vector right at head of first vector. |
|
3. For each of the following items (i) – (x). fill in blank spaces by writing the correct answer in your answer booklet.
(ii) When an arrow is drawn, it length represent_______ while arrow head show direction.
(iii) Vector we get after adding two or more vectors is called? ___________
(iv) Adding vectors by placing the tail of second vector right at the head of the first vector is called? _______
(v) Vector a + vector b = c, forming a triangle, this law is called?-___________
(vi) Velocity of a body with respect to another__________
Motion of a body with respect to another____________
(vii) One application of relative motion is___________
(viii) Lines which forms Cartesian coordinate system are called____________
(ix) Combined influence of two components is equivalent to the influence of a__________ dimension vector.
(x) a2 + b2 = c2 is _________________ law.
SECTION B:
4. Find the resultant force F when two forces 9N and 15N act on an object with angle of 60![]() between them.
between them.
5. Using parallelogram law, find resultant force when two forces 20N and 40N are acting on a object with and angle of 45![]() between them.
between them.
6. Two forces of magnitude 40N and 60N are pulling a box on a horizontal table. If the two forces make an angle of 60![]() between them, find the resultant force on box using parallelogram law.
between them, find the resultant force on box using parallelogram law.
7. Explain the following:
a) Component of vector
b) Resultant vector
c) Triangle aw of addition
d) Parallelogram law of addition
e) Relative motion
8. A body is being acted on by two forces. F1 = 18N action at an angle of 25![]() and F2 = 30N acting at 140
and F2 = 30N acting at 140![]() , from due East. Find the resultant of two forces, F, by separating the forces into x – and y – components.
, from due East. Find the resultant of two forces, F, by separating the forces into x – and y – components.
9. An aeroplane is taking off at a velocity of 20mls. Find the component of the plane’s velocity if the take off angle is
a) 70![]()
b) 45![]()
c) 60![]()
10. A river is flowing at a velocity of 2m/s due south. A person in a boat wants to move across the river at 10m/s/
a) In which direction should the person move?
b) At what velocity should the person move the boat?
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
WHATSAPP US NOW FOR ANY QUERY
App Ya Learning Hub Tanzania