THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL OF TANZANIA
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 HoursYear: 2023
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions.
- Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables and non-programmable calculator may be used.
- All communication devices and any unauthorised materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1.(a) (i) Arrange the given numbers in ascending order of magnitude:
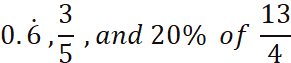
View Ans
(ii)Evaluate the expression 13 - 2 x 3 +14 ÷ (2 +5).
View Ans
(b) By listing the multiples of 2, 3 and 5, find the L.C.M of these numbers.
View Ans
2. (a) Find the values of x and y that satisfy the equations
5(x-2y) = 25
32x ÷ 3y = 34
View Ans
(b)Solve the equation 4 +3log 3 x = log 3 24.
View Ans
3. (a) Given the universal set U= {15, 30, 45, 60, 75} and the subsets A = {15, 45} and B ={30, 60}, find (A U B)’ and hence represent this information by using a Venn diagram.
View Ans
(b) (i) In a class of 50 students, 35 are boys and 15 are girls. If a student is chosen at random, what is the probability that he is a boy?
View Ans
(ii) Jonika has two shirts, blue and red. He also has three trousers, black, green and yellow. By using a tree diagram, find the probability that he will put on a blue shirt and black trouser.
View Ans
4. (a) Show that the triangle whose vertices are A(4,-4), B(-6,-2) and C(2,6) is an isosceles.
View Ans
(b) A man walks 4 km from village P to village Q and then 3 km to village R. If village Q is N60°E of village P; and village R is N30°W of village Q,
(i) represent this information on a well labeled diagram.
(ii) find the resultant displacement of the man from P to R.
View Ans
5.(a) In the following figure, RPQ = PQR and SPQ = SQP. Find the size of the angle RPS
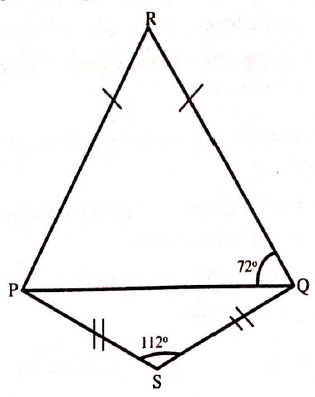
View Ans
(b) A rectangular field is 72 m long and 40 m wide. If a triangular field with a base of 60 m has an area which is equal to the area of the rectangular field, find the height of the triangular field.
View Ans
6. (a) Anna walks 24 km every day. Compute in metres, the distance she walks in 2 days.
View Ans
(b) A dealer sells mattresses whose buying price is directly proportional to the selling price. If the selling price and the buying price of one mattress are Tshs 20,000 and Tshs 18,000, respectively, find;
(i) the equation that relates the buying price and the selling price.
(ii) the new selling price when the buying price is increased by 15%.
View Ans
7. (a) Ally and Jane shared 64,000 shillings in the ratio 3:5 respectively. Find the difference between their shares.
View Ans
(b) Mr. Mrisho recorded the transactions of his business in February, 2022 in a cash account as follows:
| CASH ACCOUNT |
| DR | CR |
| Date | Particular | Folio | Amount | Date | Particular | Folio | Amount |
| February 1 | Capital |
| 1,500,000 | February 2 | Purchases |
| 1,000,000 |
| February 2 | Sales |
| 1,200,000 | February 6 | Transport |
| 200,000 |
| February 3 | Sales |
| 800,000 | February 27 | Purchases |
| 1,400,000 |
|
|
|
|
| February 28 | Balance | c/d | 900,000 |
| 1 |
|
| 3500,000 |
|
|
| 3,500,000 |
| March 1 | Balance | b/d | 900,000 |
|
|
|
|
Using the given cash account, extract the trial balance as at 28th February, 2022.
View Ans
8. (a) Write down the first four terms of a sequence whose general term is n(2n – 1) . Briefly explain whether it is an arithmetic progression or a geometric progression.
View Ans
(b) The sum of the first eleven terms of an arithmetic progression is 517. If its first term is 7, find the sum of the fourth and ninth terms.
View Ans
9.(a) A rectangular plot of land is 40 metres long. If the length of its diagonal is 50 metres, how wide is the plot?
View Ans
(b) (i) Given that A is an acute angle for which 13cos A-5 = 0 , find the value of tan A without using mathematical table.
View Ans
(ii) A triangular pond ABC is such that AB = 8 m, AC = 5 m and BAC=60 0 . Determine the length of BC .
View Ans
10. (a) If x = -3 and ��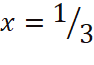 � are solutions of the equation ax2 + bx + c = 0 where a, b and c are integers, determine the values of a, b and c .
� are solutions of the equation ax2 + bx + c = 0 where a, b and c are integers, determine the values of a, b and c .
View Ans
(b) Solve the inequality 10 - x ≤ 3(x+ 10) , where x is an integer. Hence, state the first four values of x that satisfy the given inequality.
View Ans
SECTION B (40 Marks)
Answer all questions in this section.
11.The given frequency distribution table shows the scores of 30 students in a Mathematics test.
| Class interval | 40— 49 | 50— 59 | 60— 69 | 70— 79 | 80— 89 | 90— 99 |
| Frequency | 2 | 4 | 7 | 9 | 5 | 3 |
(a)Calculate the median score, correct to two decimal places.
(b)Find the mean score, correct to four significant figures.
(c)Draw a histogram and use it to estimate the mode.
View Ans
12. (a) The following figure represents a square box ABCDEFGH whose sides are 8 cm each.
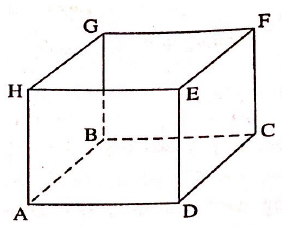
-
Determine the total surface area of the box.
-
Calculate the angle between the line segment AF and the plane ABCD, giving your answer to the nearest degree.
View Ans
(b) Boeing 787 Dream Liner flying at 500 km/h leaves Julius Nyerere International Airport in Tanzania (70 S, 45° E) at 8:00 am. When will it arrive at Addis Ababa in Ethiopia (9° N, 45° E) ? (Use the substitution ��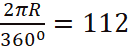 � ).
� ).
View Ans
13. (a)Find the values of x and y given that
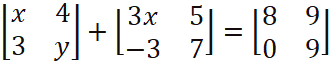
View Ans
(b) In a multiple choice test, 2 marks were awarded for each correct answer, 1 mark was deducted from each incorrect answer and 0 for not writing an answer. Anna answered 49 questions and scored 62 marks out of 100.
(i) Represent this information in a matrix form; Jetting x be the number of correct answers and y be the number of incorrect answers.
(ii) Using the inverse matrix method, determine the number of questions that Anna answered correctly.
View Ans
(c) A triangle has its vertices at the points A(1, 3), B(2, 5) and C(4,1). If the triangle is rotated through 180° anticlockwise about the origin;
(i) find the coordinates of the points A', B' and C' which are the images of A, B and C respectively.
(ii) draw the triangles ABC and A'B'C' on the same set of axes.
View Ans
14. (a)A function is defined on the set of integers as
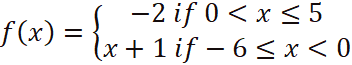
(i)Find the values of f (4) and f (-5).
(ii) State the domain and range of f (x)
View Ans
(b) The Air Tanzania Company wants to buy two types of airplanes, A and B. Type A requires 6 dam 2 of parking space, type B requires 2 dam 2 of parking space while the company has 60 dam 2 of parking space available. Also the company has 480 billion shillings and the cost for buying airplanes of type A and type B are 20 billion shillings and 30 billion shillings respectively. Find the greatest number of airplanes the company can buy.
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256