THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL OF TANZANIA CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
Time: 3hours Year: 2022
INSTRUCTIONS
- This paper consists of section A and B with a total of fourteen (14) questions
- Answer all questions
- Each question in section A carried six (06) marks while each question in section B carried ten(10) marks
- All necessary working and answers for each question must be shown clearly
- NECTA mathematical tables and non-programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room
- Write your Examination Number on every page of your answer booklet(s)
SECTION A (60 Marks)
Answer all questions in this section.
1. (a)Find the percentage of numbers which are multiples of 5 from the set [1, 2, 3, 4, . . . . . . up to 52] . Write the answer correct to one decimal place
View Ans
(b)(i)Arrange the following fractions in ascending order: 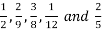
View Ans
(ii) Simplify the expression
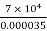 , hence write the answer in standard form.
, hence write the answer in standard form.
View Ans
2. (a)Find the value of x if 8x-1 = 16
View Ans
(b)(i)Simplify the expression 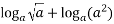
View Ans
(ii) Rationalize the denominator of the expression
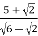
View Ans
3. (a)(i)If P ={ all multiples of 5 less than 35} and Q={all numbers between 14 and 30} find P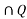
View Ans
(ii)In a village of 50 farmers, 25 grow cashew nut and 16 grow both cashew nut and maize. If 10 farmers grow neither cashew nut nor maize, find the number of famers who grow maize only. Do not use Venn diagram.
View Ans
(b)A farmer was given three seeds to germinate in a nursery. The probability that a seed will germinate is  . Using a tree diagram, find the probability that at least two seeds will germinate.
. Using a tree diagram, find the probability that at least two seeds will germinate.
View Ans
4.(a) If a = (4, 3), b=(-4, 1) and c=(2, 5), determine which of the vectors a + 2b and 3a + c is longer then the other.
View Ans
(b)If a line passing through the point (4, 2) is perpendicular to another line whose equation is 2x + 3y + 14 = 0, find the equation of the line.
View Ans
5. (a)The sides of a triangle are 4cm, 5cm and 6cm. If the longest side of a similar triangle is 18cm, find the lengths of the other sides.
View Ans
(b)(i)The perimeter of a regular hexagon inscribed in a circle is 72cm. Find radius of the circle
View Ans
(ii)The area of a triangle ABC is 70cm2. If AB= 14cm and AC=20cm, find the angle BAC
View Ans
6. (a)Anna walks 24km every day. Find, in metres, the distance she walks in 2 days.
View Ans
(b)(i)A dealer sells mattresses whose cost price (C) is directly proportional to the selling price(s). If the selling price and the cost price of one mattress are Tsh. 20,000 and Tsh. 18,000, respectively, find the constant of proportionality
(ii) By using the answer obtained in part (b)(i), determine the equation that relates the cost price and the selling price.
View Ans
7. (a)A damaged table that costs Tshs. 20,000 was sold at a loss of 15%. Find the loss made and the selling price.
View Ans
(b)Extract a Trial Balance from the following Mabala’s cash account.
| Debit | Credit |
| Date | Particular | Folio | Amount | Date | Particular | Folio | Amount |
| 5/8/2018 | Capital |
|
|
|
|
| 80,000 |
| 9/8/2018 | Sales |
|
|
|
|
| 28,000 |
| 11/8/2018 | Sales |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 82,000 |
|
|
|
|
|
|
|
| 190,000 |
| 1/9/2018 | Balance | b/d | 82,000 |
|
|
|
|
View Ans
8. (a)The fifth and eleventh terms of an arithmetic progression are 8 and -34 respectively. Find the sum of the first ten terms
View Ans
(b)A school wishes to invest Tshs. 100,000,000 in a bank which pays an interest rate of 2% compounded annually
- Find the total amount of money that will be accumulated after two years.
- Calculate the interest after two years
View Ans
9. (a)(i)Find the value of 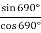 without using mathematical table
without using mathematical table
View Ans
(ii)A rectangular garden ABCD is 400m long and 300m wide. The seedlings are to be planted along the diagonal BD at equal intervals of 1.25m as shown in the following figure.
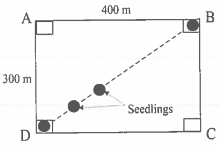
Find the number of seedlings that were planted
View Ans
(b)From the top of a tower which is 50m high, the angle of depression of a car parked on the ground is 30. How far is the car from the base of the tower? Leave the answer in surd form.
View Ans
10. (a)Express the equation 2t-10 - 3t-5 + 1 = 0 in term of x where 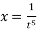
(b)From the equation you obtained in part (a), find the value(s) of x that satisfy it by using the quadratic formula.
View Ans
SECTION B (40 Marks)
Answer all questions in this section.
11. (a)Find the central angle (in degrees) made by an arc of length 22cm in a circle whose radius is 63cm. Use 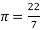 .
.
View Ans
(b) in the following figure, prove that angles x and y are supplementary given that a and b are the angles at the centre of the circle.
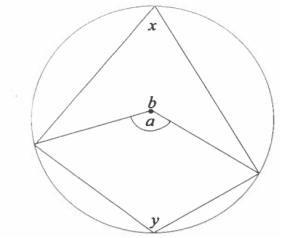
View Ans
(c)In the following figure, AC=8cm, BE=3cm and CE=4cm. find length of DE
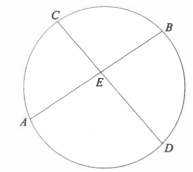
View Ans
12. (a)A bus leaves town A (3°S, 39°E) at a constant speed of 40km/h. How many hours will the bus take to reach town B (12°S, 39°E)? Use π=3.14 and radius of the Earth, R= 6,400km.
View Ans
(b)A box has a rectangular base UVXY with plane PQRS being vertically above UVXY as shown in the following figure.
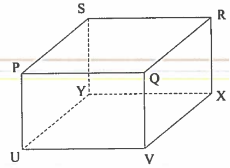
If 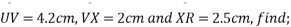
- The length of
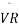 and
and 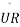 , Correct to one decimal place
, Correct to one decimal place - The angle between the diagonal
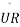 and the base UVXY
and the base UVXY
View Ans
13. (a) Find the values of x, y, z and w in the following matrix equation
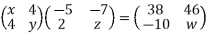 .
.
View Ans
(b)By using the matrix method, find the image of the point (3, -2) after a reflection in the line y= -x followed by another reflection in the line x=0
View Ans
(c)A translation takes point (5, 5) to the point (-7, -7). If it takes point (x, y) to (-4, -4), find the values of x and y
View Ans
14. (a)Given the function
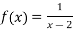 , find;
, find;
- The domain and range
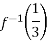
View Ans
(b)Antony wishes to buy black shirts and white shirts. He intends to buy at most black shirts. A black shirt costs Tsh. 24,000 while a white shirt costs Tsh. 30,000 and he is planning to spend up to Tsh. 180,000 for buying shirts.
- How many shirts of each kind should be bought so as to have maximum number of shirts?
- Find the greatest number of shirts that should be bought
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256