THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL OF TANZANIA
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2020
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions.
2.Answer all questions in sections A and B.
3.Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
4.All necessary working and answers for each question must be shown clearly.
5.NECTA mathematical tables and non-programmable calculator may be used.
6.All communication devices and any unauthorized materials are not allowed in the examination room.
7.Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) Simplify the expression 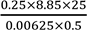 without using mathematical tables, expressing the answer correct to two significant figures.
without using mathematical tables, expressing the answer correct to two significant figures.
View Ans
(b) (i) Mr. Magani set an examination weighing a total of 96 marks with the following distribution: 20% of the marks were awarded for reading, 40% for writing, 15% for practical and the remaining percentage for spelling. Find the marks that were awarded for spelling.
View Ans
(ii) Three airplanes arrived at Kilimanjaro International Airport (KIA) at the intervals of 30 minutes, 40 minutes and 55 minutes. If all three airplanes arrived at KIA at 2:00 p.m. on Saturday, when and at what time would they arrive together again?
View Ans
2. (a) If 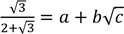 , find the values of a, b and c.
, find the values of a, b and c.
View Ans
(b) (i) Solve equation 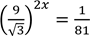
View Ans
(ii) Given log2=0.3010 and log3 =0.4771, find value of 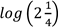
View Ans
3. In a certain school, 40 students were asked about whether they like tennis or football or both. It was found that the number of students who like both tennis and football was three times the number of students who like tennis only. Furthermore, the number of students who like football only was 6 more than twice the number of students who like tennis only. However, 4 students like neither tennis nor football.
(a) Represent this information in a Venn diagram, letting x be the number of students who like tennis only. (b) Use the results obtained in part (a) to determine the probability that a student selected at random likes;
(i)Football only.
(ii)Both football and tennis.
View Ans
4. (a) (i) A line whose gradient is 3/ 2 has the x-intercept of - 3. Find the equation of the line in the form y=mx + c , where m and c are constants.
View Ans
(ii) Find the length of a line segment joining the points (3,-2) and (15,3) .
View Ans
(b) A boat sails due to North at speed of 120km/h and wind blows at speed of 40km/h due to east. Find actual speed of the boat. Use 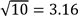
View Ans
5.(a) In the following triangle ABC, AB=8cm, BC=11.3cm and angle ABC=300. Find area of triangle ABC.
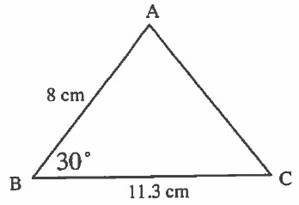
View Ans
(b)(i) Find he perimeter of a regular hexagon inscribed in a circle whose radius is 100 m.
View Ans
(ii) Given that
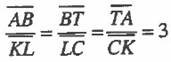
where AB,BT and TA are sides of triangle ABT and KL, LC and CK are sides of triangle KLC. What does this information imply?
View Ans
6(a) The variables t and z in the following table are related by the formula z = atn where a is a constant and n is a positive integer.
(i)Use the data from the table to determine the values of a and n.
(ii)Use the values of a and n obtained in part (a) (i) to complete the following table
View Ans
(b) If v varies directly as the square of x and inversely as 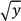 , given that v =18 when x = 3 and y =16 , find the value of v when x = 5 and y = 4.
, given that v =18 when x = 3 and y =16 , find the value of v when x = 5 and y = 4.
View Ans
7.(a)(i) A school has 2,000 students, of whom 1,500 are boys. What is the ratio of boys to girls in the school?
View Ans
(ii) Matiku bought a book for Tshs. 120,000. A year later, he sold the book at a profit of 20%. What was the selling price of the book?
View Ans
(b) Halima started a business o 1st September, 2018 with a capital of Tshs. 25,0001= in cash.
September 2, bought goods for cash 15,0001=
3, sold goods for cash 3,0001=
5, sold goods for cash 5,0001=
6, paid carriage on goods 5001=
9,sold goods for cash 14,000/=
15, bought goods for cash I ,000/=
19 , paid rent 2,0001=
20, purchased goods 6,0001=
27, paid wages 5,000/=
28, sold goods on credit 1,000/=
By using these transactions, prepare the cash account
View Ans
8. (a) Find the first term and the common difference of an arithmetic progression whose 5th term is 21 and 8th term is 30.
View Ans
(b) Find the 10th term of a sequence whose first three consecutive terms are 5, 15 and 45. (Leave the answer in exponent form).
View Ans
9. (a) In the following figure, AP is perpendicular to BC , AB= 13cm, BP = 5 cm and AC =.15 cm.
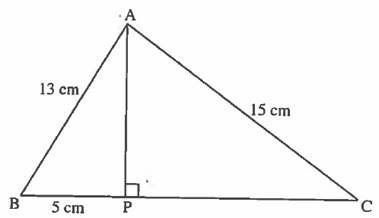
Calculate the lengths of AP and CP .
View Ans
(b) From the top of a building 75 m high, John sees a lorry and a minibus along the road, both being on one side of the building at the angles of depression of 300 and 600 respectively.
(i)Sketch a diagram representing this information.
(ii)Determine the distance between the cars, leaving the answer in surd form.
View Ans
10. (a) Rachel is three years older than her brother John. Three years to come, the product of their ages will be 130 years. Formulate a quadratic equation representing this information. Hence, by using the quadratic formula, find their present ages.
View Ans
(b) The sum of square of two consecutive positive number is 61. Find the numbers.
View Ans
SECTION B(40 Marks)
Answer All Questions In This Section
11.The following data represent the marks scored by 36 students of a certain school in geography examination.
| 72 | 76 | 90 | 89 | 74 | 82 | 63 | 74 | 70 |
| 73 | 58 | 71 | 55 | 62 | 65 | 74 | 71 | 64 |
| 71 | 85 | 70 | 61 | 64 | 75 | 51 | 83 | 50 |
| 61 | 83 | 68 | 70 | 80 | 50 | 60 | 66 | 68 |
(a)Prepare a frequency distribution table representing the given data by using the class intervals: 50 - 54, 55 -59, 60 - 64, and so on.
(b)Use the frequency distribution table obtained in part (a) to:
(i)Draw a histogram.
(ii)Calculate the median. Write the answer correct to 2 decimal places.
View Ans
12. (a) Two towns, A and B, are located at (100S, 380E) and (100S, 430 E) respectively.
(i)Find the distance between the two towns in kilometers. (Use radius of the Earth, R = 6400 km and 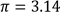 .Give the answer to the nearest whole number.
.Give the answer to the nearest whole number.
(ii)Suppose a ship is sailing at 50 km/h from town A to town B. Using the answer obtained in part (a) (i), find how long will the ship take to reach town B.
View Ans
(b) The following figure represents a rectangular prism in which PQ =12 cm, QR=8cm and RY=4cm.
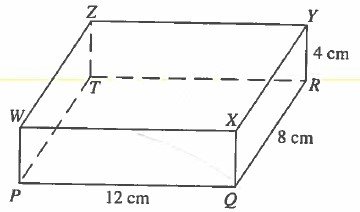
Find;
(i)The total surface area.
(ii)The angle between the planes PTZW and QRZW .
View Ans
(c) Calculate the volume of a cone whose base radius is 12 cm and slant height is 20 cm. (Use 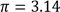 ).
).
View Ans
13. The inverse of matrix A is
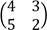
Find matrix A.
View Ans
(b) Amani and Asha bought Coca-cola and Pepsi drinks for a farewell party. Amani spent Tshs. 9950 to buy 12 bottles of Coca-cola and 5 bottles of Pepsi drinks. Asha spent Tshs. 8150 to buy 9 bottles of Coca-cola and 5 bottles of Pepsi drinks. Formulate a system of linear equations and hence apply the matrix method to find the price of one bottle of each type of the drinks.
View Ans
(c) Point A(4, 2) is reflected in the line y + x = 0 followed by an anticlockwise rotation through 90° about the origin. Find the final image of point A.
View Ans
14.(a) Suppose a function f is defined by f (x) = (x + 2)2 , find the domain and range of the inverse of the function f .
View Ans
(b) A businessman plans to buy at most 210 sacks of Irish and sweet potatoes. Irishpotatoes cost shs. 30,000 per sack and sweet potatoes cost shs. 5,000 per sack. He can spend up to shs. 2,500,000 for his business. The profit on a single sack of Irish potatoes is shs. 12,000 and for sweet potatoes is shs. 10,000. How many sacks of each type of potatoes the businessman will buy in order to realize the maximum profit?
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256