THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For School Candidates Only)
Time: 3 Hours Tuesday, 9hOctober 2012 a.m.
Instructions
1. This paper consists of sections A and B.
2. Answer all questions in section A and four (4) questions from section B. Each question in section A carries 6 marks while each question in section B carries 10 marks.
3. All necessary working and answers for each question attempted must be shown clearly.
4. Mathematical tables may be used.
5. Calculators and cellular phones are not allowed in the examination room.
6. You are advised to spend not more than two (2) hours on section A and the remaining time on section B.
7. Write your Examination Number on every page of your answer booklet(s).
8. The following constants may be used:
(a) The radius of the earth R = 6370km
(b) π = 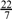
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) By using mathematical tables, evaluate 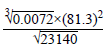 to three significant figures.
to three significant figures.
View Ans
(b) Rationalize 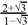
View Ans
2. (a) Find the value of x for which 2x ? 16 = 81x
View Ans
(b) Solve loga(x2 + 3) − logax = 2loga2
View Ans
3. (a) Mr. Bean lived a quarter of his life as a child, a fifth as a teenager and a third as an adult. He then spent 13 years in his old age. How old was he when he died?
View Ans
(b) A and B are subsets of the universal set U . Find n(A∩B) given that n(A) = 39, n(A′∩B′) = 4, n(B′) = 24 and n(U) = 65 .
View Ans
4. Given that a = (3, 4), b = (1, 4) and c = (5,2) determine:
(a) d = a + 4b – 2c ?
(b) magnitude of vector d , leaving your answer in the form m√n ?
(c) the direction cosines of d and hence show that the sum of the squares of these direction cosines is one.
View Ans
5. (a) If polygons X and Y are similar and their areas are 16cm2 and 49cm2 respectively, what is the length of a side of polygon Y if the corresponding side of polygon X is 28cm?
View Ans
(b) (i) Show whether triangles PQR and ABC are similar or not
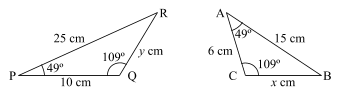
(ii) Find the relationship between y and x in the triangles given above.
View Ans
6. (a) The power(P) used in an electric circuit is directly proportional to the square of the current (I).
When the current is 8 Ampere (A), the power used is 640 Watts (W).
(i) write down the equation relating the power (P) and the current (I).
View Ans
(b) If x * y is defined as 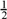 (x + y), find (5 *− 2) * (3 *− 4) .
(x + y), find (5 *− 2) * (3 *− 4) .
View Ans
7. (a) By selling an article at shs. 22,500/= a shopkeeper makes a loss of 10%. At what price must the shopkeeper sell the article in order to get a profit of 10% ?
View Ans
(b) An alloy consists of three metals A, B and C in the proportion A : B = 3 : 5 and B : C = 7 : 6 Calculate the proportion A : C.
View Ans
8. (a) If the 5th term of an arithmetic progression is 23 and the 12th term is 37, find the first term and the common difference.
View Ans
(b) Find the sum of the first four terms of a geometric progression which has a first term of 1 and a common ratio of 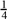 .
.
View Ans
9. (a) Find the length AC from the figure below:
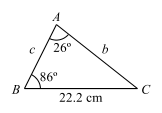
View Ans
(b) A ladder reaches the top of a wall 18m high when the other end on the ground is 8m from the wall. Find the length of the ladder.
View Ans
10. (a) Solve for x if x−64 = 1 + 4x
View Ans
(b) If the sum of two numbers is 3 and the sum of their squares is 29, find the numbers.
View Ans
SECTION B (40 Marks)
Answer any four (4) questions from this section.
11. Anna and Mary are tailors. They make x blouses and y skirts each week. Anna does all the cutting and Mary does all the sewing. To make a blouse it takes 5 hours of cutting and 4 hours of sewing. To make a skirt it takes 6 hours of cutting and 10 hours of sewing. Neither tailor works for more than 60 hours a week.
(a) For sewing show that 2x + 5y ≤ 30
(b) Write down another inequality in x and y for the cutting.
(c) If they make at least 8 blouses each week, write down another inequality.
(d) Using 1cm to represent 1 unit on each axis, show the information in parts (a), (b) and (c) graphically. Shade only the required region.
(e) If the profit on a blouse is shs. 3,000/= and on a skirt is shs. 10,000/=, calculate the maximum profit that Anna and Mary can make in a week.
View Ans
12. In a survey of the number of children in 12 houses, the following data resulted: 1, 2, 3, 4, 2, 2, 1, 3, 4, 3, 5, 3
(a) Show this data in a frequency distribution table.
(b) Draw a histogram and a frequency polygon to represent this data.
(c) Calculate the mean and mode number of children per house.
View Ans
13. (a) An open rectangular box measures externally 32cm long, 27cm wide and 15cm deep. If the box is made of wood 1cm thick, find the volume of wood used.
View Ans
(b) Find the distance (in km) between towns P(12.4°S, 30.5°E) and Q(12.4°S, 39.8°E) along a line of latitude, correctly to 4 decimal places.
View Ans
14. (a) The following balances were extracted from the ledgers of Mr. and Mrs. Mkomo business on 31st January. Prepare a trial balance.
Capital 30,000/= Insurance 3,000/=
Furniture 25,000/= Cash 18,000/=
Motor vehicle 45,000/= Discount received 7,000/=
Sales 68,000/= Discount allowed 4,000/=
Purchases 54,000/= Drawing 12,000/=
Creditors 76,000/= Electricity 5,000/=
Debtors 15,000/=
View Ans
(b) Determine the gross profit and the net profit from the information given below.
Sales 38,000/=
Opening stock 8,000/=
Purchases 25,000/=
Electricity 4,000/=
Discount allowed 2,000/=
Closing stock 5,000/=
View Ans
15.(a) Find the value of k such that the matrix 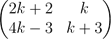 is singular.
is singular.
View Ans
(b) The vertices of ABC are A(1,2) , B(3,1) and C(− 2,1). If triangle ABC is reflected on the xaxis, find the coordinates of the vertices of its image.
View Ans
(c) Solve the following simultaneous equations by matrix method.
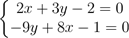
View Ans
16. A box contains 7 red balls and 14 black balls. Two balls are drawn at random without replacement.
(a) Draw a tree diagram to show the results of the drawing.
(b) Find the probability that both are black.
(c) Find the probability that they are of the same colour.
(d) Find the probability that the first is black and the second is red.
(e) Verify the probability rule P(A) + P(A′) = 1 by using the results in part (b).
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256