THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041 BASIC MATHEMATICS
(For School Candidates Only)
Time: 3 Hours Monday, 3rdOctober 2011 a.m.
Instructions
1. This paper consists of sections A and B.
2. Answer all questions in section A and four (4) questions from section B. Each question in section A carries 6 marks while each in section B carries 10 marks.
3. All necessary working and answers for each question done must be shown clearly.
4. Mathematical tables may be used.
5. Calculators and cellular phones are not allowed in the examination room.
6. You are advised to spend not more than two (2) hours on section A and the remaining time on section B.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section showing all necessary working and answers.
1. (a) Express 0.05473
(i) correct to three (3) significant figures
(ii) correct to three (3) decimal places
(iii) in standard form.
View Ans
(b) Evaluate
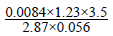
without using mathematical tables and express the answer as a fraction in its simplest form.
View Ans
2. (a) Solve the equation log45x − log4(x + 2) − log43 = 0
View Ans
(b) By rationalizing the denominator, simplify the following expression.
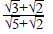
View Ans
3.(a) A shopkeeper sold 500 sweets. Some costs shs. 5 and some cost shs. 8. The cash received for the more expensive sweets was shs. 100 more than for the cheaper sweets. Find the number of each kind of sweet which were sold.
View Ans
(b) A survey of 240 houses showed that all of them kept a farm or a garden or both. If 180 kept gardens and 79 kept farms, how many houses kept both?
View Ans
4. (a) Find the distance between point (− 3,− 2) and the point midway between (2,13) and (4,7). Write your answer in the form a√c where a and c are positive real numbers.
View Ans
(b) Given the vectors x = 3i + 2j, y = 5i – 3j and z = 4i – 2j
(i) Find the resultant vector r = x + y + z and its direction.
(ii) Plot the three vectors on the same axes and hence indicate the magnitude of each vector [do not perform any calculation].
View Ans
5.(a) In figure 1, ABCD is a square. If AR = BR prove that R is the midpoint of DC
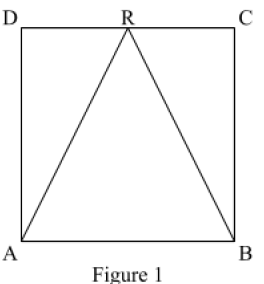
View Ans
(b) Calculate the size of an interior angle of a regular nonagon.
View Ans
6. The number of square tiles needed to surface the floor of a hall varies inversely as the square of the length of a side of the tile used. If 2016 tiles of side 0.4m would be needed to surface the floor of a certain hall, how many tiles of side 0.3m would be required?
View Ans
7. The ratio of men : women : children living in Mkuza village is 6 : 7 : 3. If there are 42,000 women, find how many:
(a) (i) children live in Mkuza village
(ii) people altogether live in Mkuza village.
(b) The 42,000 women is an increase of 20% on the number of women 10 years ago. How many women lived in the village?
View Ans
8. (a) If the first term of an arithmetic progression is 3 and the third term is 13, find the second term, the fourth term and the sum of the first ten terms.
View Ans
(b) A certain geometric progression has a common ratio of 2 and the sum of the first five terms is 155. Find the first term and give the formula for the nth term.
View Ans
9. Figure 2 represents plotting of two stations A and B which are 4,000m apart. T is a stationary target in the same vertical plane as A and B. When the distance from station A is 10,000m, the angle of elevation is 30°.
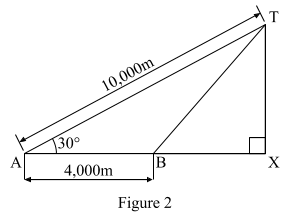
Calculate
(a) The vertical height of the target, TX
(b) The distance AX , BX and TB
(c) The angle of elevation of the target, T , from B
View Ans
10. (a) Find the solution of the quadratic equation 8x2 − 34x + 21 = 0 by using the factorization method.
View Ans
(b) Solve for x if
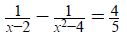
View Ans
SECTION B (40 Marks)
Answer any four (4) questions from this section. Extra questions will not be marked.
11. The number of units of proteins and starch contained in each of two types of food A and B are shown in the table below:
| Type of Food | Units of Protein Per kg | Units of Starch Per kg | Cost per kg |
| A | 8 | 10 | 400/= |
| B | 12 | 6 | 500/= |
| Minimum Daily Requirement | 32 | 22 |
|
What is the cheapest way of satisfying the minimum daily requirement?
View Ans
12. The following table gives the scores of sixty students in a Basic Mathematics test.
| Scores | Frequency |
| 0 – 10 | 5 |
| 10 – 20 | 7 |
| 20 – 30 | 15 |
| 30 – 40 | 25 |
| 40 – 50 | 8 |
Calculate:
(a) The mean score if the assumed mean is obtained from the mid mark of the modal class?
(b) The median?
(c) The range.
View Ans
13. In figure 3, ABCD is a rectangle in which AB = 3cm and BC = 2cm. V is a point such that
VA = VB = VC = VD = 6cm and AO = OC . Find:
(a) The angle VAD?
(b) The length of AC ?
(c) The angle between VA and the plane ABCD.
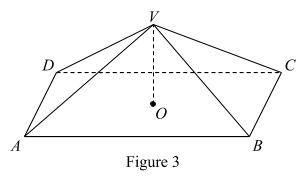
View Ans
14. Study the given trial balance and answer questions that follow:
Trial Balance as of 31 December 2007
| S/N | Details | Amount (Tshs) | Amount (Tshs) |
| 1 | Cash | 185,000.00 |
|
| 2 | Capital |
| 200,000.00
|
| 3 | Purchases
| 110,000.00
|
|
| 4 | Sales |
| 104,000.00 |
| 5 | Water bills | 3,000.00
|
|
| 6 | Advertising | 2,000.00 |
|
| 7 | Telephone bills | 1,000.00 |
|
| 8 | Salaries | 3,000.00 |
|
|
|
| 304,000.00 | 304,000.00 |
Prepare the following for the year ending 31 December 2007:
(a) Trading account?
(b) Profit and loss account?
(c) Balance sheet.
View Ans
15. (a) Reflect the point (1,2)in the line x + y = 0.
View Ans
(b) Find the enlargement matrix which maps the point (− 3,4) into (18,− 24).
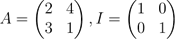
View Ans
(c) It is given that and k is a real number.
(i) Find the matrix A − kI
(ii) Show that the matrix in c(i) above has no inverse if k2 − 3k − 10 = 0
View Ans
16. Draw a graph of the function y = x2 − 3x + 2 for the values of x from − 2 to 5.
From your graph, find:
(a) The range of the function?
(b) The minimum value of y and the value of x at which this minimum value occurs?
(c) The solution of the equation x2 − 3x − 4 = 0
(d) The solution of the inequality x2 − 3x + 2 > 0
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256