THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL OF TANZANIA
FORM TWO NATIONAL ASSESSMENT
041 BASIC MATHEMATICS
Time: 2:30 Hours Tuesday, 12 th November 2019 a.m.
Instructions
1. This paper consists of ten (10) compulsory questions.
2. Show clearly all the working and answers in the space provided.
3. All writing must be in blue or black ink except drawings which must be in pencil.
4. Four figure mathematical tables, geometric instruments and graph papers may be used where necessary.
5. All communication devices, calculators and any unauthorized materials
are not allowed in the examination room.
6. Write your Examination Number at the top right hand corner of every page.
1. (a) Find the Greatest Common Factor (GCF) of 18, 24 and 60. 1(a) GCF of 18, 24 and 60
View Ans
1(b) population of three towns are 65,600, 13,400 and 29,700 to approximate total to the nearest thousands
View Ans
2(a) Rehema spent 1/8 of her salary on transport and 1/4 on food. If she remained with sh. 80,000, what was her salary?
View Ans
2. (b) Change 5/8 into:
(i) percentage.
(ii) decimal
View Ans
3(a) A machine that costs sh. 180,000 was sold at a profit of 40%. Find the selling price.
View Ans
3(b) A father divided sh. 150,000 among Rose and Japheth in the ratio 2:3 respectively. How much money did each get?
View Ans
4(a) Use the following figure to find the value of a + b + c .
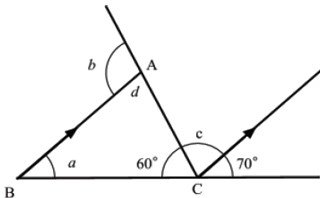
View Ans
4(b)The perimeter of triangle ABC is 16 cm . If AB= (5 + x ) cm, AC = (2 + x ) cm and BC= 5 cm, find the value of x and hence the actual lengths of ABand AC .View Ans
5(a) Solve x + y = 4
2x − y = 5
By using the substitution method.
View Ans
5(b) Find two consecutive positive numbers such that the sum of their squares is equal to 145.
View Ans
6(a)If the gradient of the straight line ky = kx + x + 7 is 2,
find: (i) the value of k ,
(ii) the y -intercept.
View Ans
6(b) By using a sketch, find the image of point A(2,3) after a reflection in the line y = x followed by another reflection in the line y = - x .
View Ans
7. (a) Solve for n in the equation 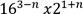 =1/2
=1/2
View Ans
7(b) Find the value of x in the equation log (2 x + 1) + log 4 = log (7 x + 8).
View Ans
8(a) In the following figure, AB = DC and ABC = . Prove that . ΔABC = ΔDCB
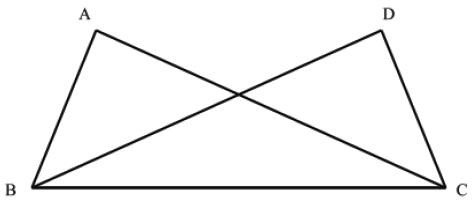
View Ans
8(b) If ΔABC ~ ΔPQR and AC = 20 cm, PR = 10 cm, QR = 12 cm and PQ = 9 cm, find the lengths of AB and BC .
View Ans
9(a) Use the following figure to find the values of x and y .
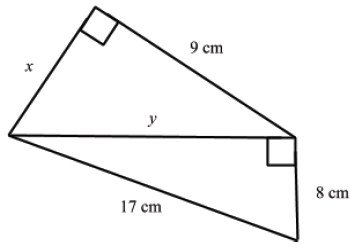
View Ans
9(b) Find the value of each of the following expressions and simplify the answer. (i) sin 60 °(cos 45° + sin 30°), (ii) tan 45 °(4cos 60° − √3 tan 30°).
View Ans
10(a) In a class of 35 students, 21 study commercial subjects, 15 study both commercial and science subjects and 4 students study science subjects only. Use a Venn diagram to find the number of students who study:
(i)either science or commercial subjects.
(ii) neither science nor commercial subjects.
(iii) commercial subjects only. (iv) science subjects.
View Ans
10(b) The following pie chart represents the distribution of form two students who were selected to participate in sports activities. If there are 200 students who were selected, how many students participate in each activity?
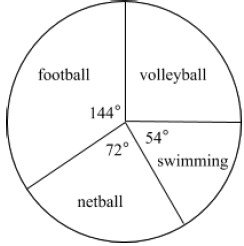
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256