CHRISTIAN SOCIAL SERVICES COMMISSION- (CSSC) WESTERN ZONE
FORM TWO JOINT EXAMINATION

CODE: 041 BASIC MATHEMATICIS
TIME: 2:30 HRS Date: 29th August, 2023
INSTRUCTIONS
- This paper consists of ten (10) compulsory questions each question carries ten (10) marks
- Show clearly all the WORKING and ANSWERS in the space provided.
- All writing must be in blue or black ink EXCEPT drawings which must be in pencil
- Mathematical tables, geometrical instruments and graph papers may be used where necessary
- Cellular phones, calculators and any unauthorized materials are NOT ALLOWED in the assessment room.
- Write your Assessment Number at the top right comer of every page.
| FOR ASSESSOR’S USE ONLY | ||
| QUESTION NUMBER | SCORES | ASSESSOR’S INITIALS |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| TOTAL | ||
| CHECKER’S INITIALS | ||
- Find the difference between the LCM and GCF of the number 21,35 and 56
(b) Given that x=3.8324, y=0.![]() and z=10.04. By rounding each number to three significant figures, find the value of
and z=10.04. By rounding each number to three significant figures, find the value of ![]() and write your answer to two decimal places
and write your answer to two decimal places
- A dog, a cat and a goat have masses of 30.75kg, 13.44kg and 48.26kg, respectively
- Calculate the total mass of all three animals
- Convert the answer obtained in (a) (i) into grams
(b) Round off
- 75000 correct to 2 significant figures
- 0.00015 to 4 decimal places
- 28.82 to tens
Hence estimate the value of ![]()
- (a) Given that
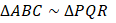 ,find the value of A
,find the value of A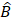 C if ABC M= 1200and PRQ= 250
C if ABC M= 1200and PRQ= 250
(b) Find the area of isosceles triangle whose base is 10 cm and one of the equal sides is 13. cm
- Solve the following simultaneous equations by elimination method:
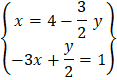
(b) The sum of the reciprocal of two consecutive even numbers is ![]() . Find the numbers.
. Find the numbers.
- (a) Mabala want to invest some amount of money so that its value after 4 years will be 812000/=. How much should the investor invest at 4% per amount on simple interest?
(b) Two numbers are in the ratio of 2:3. If 5 is added to both numbers, the resulting numbers are in the ratio of 3:4. Find the original numbers.
- What value of T will make the gradient of the line passing through the points
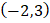 and
and 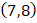 equal to that passing through the points
equal to that passing through the points 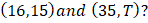
(b) The translation T maps the point ![]()
- (a) Rationalize the denominator of the expression
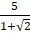
(b) Evaluate without using mathematical table
![]()
![]()
![]() 8. In the figure below, if
8. In the figure below, if ![]() //
//![]() ,
,![]() ,
, ![]() and
and ![]() : prove that ADE ≈ ABC
: prove that ADE ≈ ABC
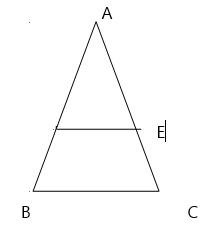
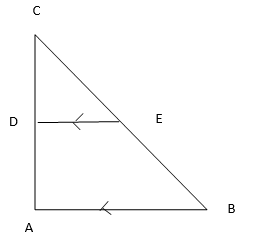
(b) Find the value of x
9.Without using mathematical table, evaluate:
![]()
(b) A rhombus has diagonals of 12cm and 16cm respectively. Find its sides
10.The universal set ? has subsets A and B. given that ![]()
Find:
- n
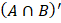
(b) The following table shows the marks which were recorded by 48 form two students in a mathematics test at Zimbiri Secondary School.
| Marks | 40 | 45 | 50 | 55 | 60 | 65 | 70 |
| No. of students | 6 | 8 | m | 5 | 9 | 4 | 3 |
- Determine the value of m
- What was the number of students who scored 55% and above?
- What was the lowest mark?
- What mark was scored by the majority of these students?
- If 55% was the pass mark, how many students failed this test?
FORM TWO MATHEMATICS EXAM SERIES 75
FORM TWO MATHEMATICS EXAM SERIES 75
Number……………………………
 | THE UNITED REPUBLIC OF TANZANIA MBEYA CITY COUNCIL ACADEMIC COMMITTEE FORM TWO PRE-MOCK II EXAMINATION |  |
CODE: 041 BASIC MATHEMATICS
Time: 02:30 HRS Monday, 15th May 2023 a.m.
- This paper consists of ten (10) compulsory questions
- Answer all questions by showing your solution very clearly
- Al writings mast be in blue or black ink except drawings which must be in pencil.
- NECTA Mathematical tables, geometric and graph paper may be used where necessary.
- Write your examination number on every page of your answer sheet(s).
| FOR EXAMINER’S USE ONLY | ||
| QUESTION NUMBER | ||
| SCORE | EXAMINERS INITIALS | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| TOTAL |
| |
| CHECKER’S INITIALS | ||
1.(a) (i) Add the first three multiples of 2, 3 and 5.
(ii) The numbers K, 2, 3 and 5 have an average of 5. What is the number represented by the letter K?
(b) Re-write the number ![]() as a mixed fraction.
as a mixed fraction.
2. (a) The number of pupils in three primary schools is as follows. Iganzo primary school is 1600 pupils, Ruanda primary school is 1500 pupils and Ilea primary school is 1800 pupils. Approximate the number of pupils of the three schools to the nearest thousands.
(b) Calculate ![]()
3. (a) Study carefully the figure below
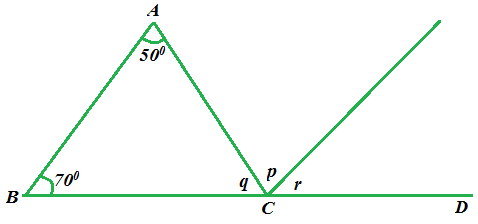
- Find the values of the angles marked p, q and r respectively.
- Find the value of
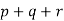
(b) If ![]() and
and ![]() are supplementary angles, determine the value of
are supplementary angles, determine the value of ![]() .
.
4. (a) One - third of the sum of ages of Ana and Asha is 50 years, and one - fifth of the difference of their ages is 2 years, find the age of Ana and Asha respectively.
(b) The width of the football ground is 40m. If the area of the same football ground is ![]() ;
;
(i) find the length of the football ground
(ii) if the person has to walk around the football ground, what length of the football ground is expected to be covered by the person?
5. (a) A car was sold at a profit of 90000 shillings. If the rate of profit is ![]() % , find the purchasing price of the car and its selling price?
% , find the purchasing price of the car and its selling price?
(b) Mr. Juma deposited a certain amount of money in a bank for a period of 3 years at the rate of 3.5% which gives an interest of 8400 shillings. Determine the amount of money that Mr. Juma deposited initially.
6. (a) (i)If the straight line CD which is passing through the points C (2 , 6) and D ( K , 3 ) has a gradient of -1, find the value of K.
(ii) ) Find equation of a line passing through point ( 0 , 3 ) and ( 1 , 2 )
(b) Expand the following expressions
(i) ![]()
(ii) ![]()
7. (a) Given that ![]() and
and ![]() , determine the value of
, determine the value of
(i) ![]()
(ii)![]()
(b) (i) given that ![]() , determine the values of
, determine the values of ![]() and
and ![]() respectively.
respectively.
(ii) express ![]() into radical form.
into radical form.
(iii) express (![]() )4 as a single exponent
)4 as a single exponent
8. (a) Find the value of ![]() for the logarithmic equation below
for the logarithmic equation below
![]()
(b) Simplify the expression ![]() and give your answer in standard form.
and give your answer in standard form.
9. (a) If the two sides of the right angled triangle are ![]() and
and ![]() . Find the value of the letter
. Find the value of the letter ![]() if the hypotenuse is
if the hypotenuse is ![]() .
.
(b) (i) If M*N = M2 + √N, find value of x given that 4*x = 10
(ii) Rationalize the denominator to the simplest form: ![]()
10. (a) Draw a Venn diagram to represent the relationship between the sets A= {1,2,5,6,7,9,10} and B={1,3,4,5,6,8,10}
(b) (i) Given the two quadratic equation y2 + xy – r = (y + 2) (y – 3), find the value of x and r
(ii) solve the value of p: 2p2 – 8p + 8 = 0 (use general formular of quadratic equation)
FORM TWO MATHEMATICS EXAM SERIES 66
FORM TWO MATHEMATICS EXAM SERIES 66
PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
MOROGORO REGION
FORM TWO ASSESSMENT
Basic mathematics
Code: 041
Time: 2.30: hours
Instructions
- This paper consists of ten (10) questions.
- Cellular phones and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer
1. (a)(i) Write in numerals: six hundred thousand sixty six.
(ii) In a school, there is a menu that have already prepared for students. According to the menu, every 5 days mango fruit is provided for lunch, every 4 days fish, and every 9 days mixed salad. If today all the three types of food given above are all in the today’s menu, after how many days will all the three types of food again be found together in the menu
(b)(i)Change ![]()
(ii)Anishiye scored 27 marks out of 45 score in mathematics test. What percentage was this?
2. (a) The weight of one female student at Maanga Primary School is 50kg and 750g. If there are 210 students of the same weight, find their total weight.
(b) Approximate 13.95 and 9.72 to the nearest tens, hence evaluate 13.95 x 9.72 by using the approximated number
3. (a)The length of one side of side of rectangle is 3 times the width of it. If the perimeter of the rectangle is 24cm. Find the exact length and width of the figure.
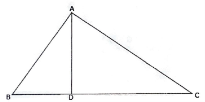
(b)In the given figure below angle BAC is 90° and AD is perpendicular to BC. Find thr number of right triangles in the given figure.
- (a)Make w the subject
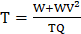
(b) Solve 3x2 + 30x + 9 = 0 by completing the square. Leave your answer in surd form.
5. (a)Ashira went to Makunguru market and bought a pairs of shoes for her child for Tshs 35000 and sold it after three days to Mwanaidi for Tsh 50000/= Calculate the percentage profit obtained.
(b)Juma, Ali and David are aged 12, 14 and 20 years respectively. They are to share Tsh. 69,000,000 in the ratio of the ages. How much money will each get?
6. (a)If a line through (P, 2) and (3, -1) have a slope of -0.75. find the value of p
(b)Triangle ABC with vertices A(1,0) B(4,-2) and C(3,2) is enlarged by scale factor of 2 and then reflected in the line y-x=0. Sketch the object and image on the same xy plane.
7. (a) Rationalize the denominator ![]()
(b) If ![]() , find value of x
, find value of x
8. (a)Triangle XYZ is similar to triangle ABC, and XY=8cm, if the area of Triangle XYZ is 24cm2 and the area of the triangle ABC is 96cm2 calculate the length of AB
(b)(i)Give two properties of congruent triangles
(ii) If two angles A and B are congruent angles. If the measure of angle A is 45°calculate the measure of angle B
9. (a) Two friends are meeting at a playground. Mary is already at the park but her friend Bob needs to get there taking the shortest path as possible. Bob has two ways he can go – he can follow the roads getting to the park, first heading south 15km, then heading west 20km. The total distance covered following the roads will be 35km. The other way he can get there is cutting through some open fields and walk directly to the park. Find the distance of cutting through some open space to reach at a pack.
(b)A ladder of length 12m is set against a vertical wall. If it makes an angle of 28° with the wall, how far up the wall does it reach?
10. (a)In a class of 20 students, 12 students study chemistry but not physics, 4 students study physics but not chemistry and 1student study neither physics nor chemistry. How many students study physics in the class?
(b)The scores of a Civics test at Loleza Girls secondary school taken by students were recorded as follows:
56,30,21,49,34,58,22,38,27,31,35,41,53,25,34, 26,52,32,63,25,50,36,29,34,21,61,33,51,20,41, 48,33,58,20,34,30,50
- Construct frequency distribution table starting with the classes 20 – 24, 25 – 29 .......
- Find number of students who did the test
- If the pass mark was 50%, How many students pass the test
- Draw the histogram
FORM TWO MATHEMATICS EXAM SERIES 64
FORM TWO MATHEMATICS EXAM SERIES 64
 | PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT MVOMERO DISTRICT COUNCIL |  |
FORM TWO MOCK EXAMINATION
041 BASIC MATHEMATICS
TIME: 2:30 Hours MAY 2023
INSTRUCTIONS
- This paper consists (10) questions
- Answer all questions
- Each question carries ten (10) marks
- All necessary working and answer for each question must be shown clearly
- NECTA mathematical tables and non- programmable calculators may be used
- All communication devices and any unauthorized material are not allowed in the examination room
- Write your examination Number on every page of your answer sheet(s)
1. (a) Mr. John has three classes. Each class has 28, 42 and 56 students respectively. Mr. John wants to divide each class into groups so that every group in every class has the same number of students and there are no students left over. What is the maximum number of students Mr. John can put into each group?
- If x = 0.
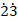 and
and 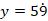 express
express 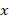 and
and 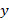 in the form of
in the form of 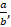 where by
where by 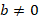 , “
, “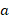 ” and “
” and “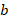 ” are integers, then find the value of
” are integers, then find the value of 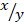 .
.
2. (a) write 490.032578 correct to
- 5 significant figures
- Thousandths
- 4 decimal places
- A lorry carries 7.2 tonnes of sand form the mining area to industrial site on the way 230kg of sand fall off away. What is the remaining mass at the end of the journey?
3. (a) The interior angle of a regular polygon is four times as its exterior angle. Find
- The size of each exterior angle
- The number of sides
- State the name of a polygon
- The perimeter of a rectangle is 20cm and its area is 24cm2. Calculate the length and breadth of the rectangle.
4. (a) The sum of numbers of boys and girls in a class is 36. If twice the number of girls exceeds the number of boys by 12. Find the number of boys and girls in the class.
- Quadratic equations can be solved by several methods and one of them is completing the square method. Hence solve the equation
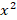 =
=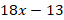 by completing the square.
by completing the square.
5. (a) In a certain boarding school in coastal island there were 500 students. The ratio of boys to girls is 3:2. How many more boys than girls are there in school?
- Find the principal that will earn 90,000/= in 5 years at the rate of 4
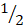 % per annum.
% per annum.
6. (a) The line through the point A ![]() and B
and B ![]() has equal slope to that
has equal slope to that
![]() . Find the value of K.
. Find the value of K.
- The scale of the map is given by 1:50,000. Calculate the ground distance which is represented by 4.8cm on the map.
7. (a) Solve the following exponential equation![]() =
=![]()
- Given that
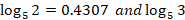 =0.6826, find
=0.6826, find 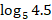
8. (a) Use the figure below to prove that B![]() D = B
D = B![]() D
D
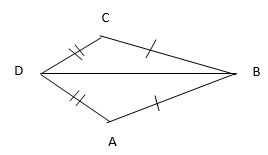
- If
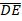 //
//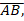 prove that
prove that 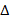 CDE is similar to
CDE is similar to 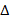 CAB
CAB
9. (a) A painter placed 20m ladder against the wall of a house so that the base of the ladder is 4m away from the wall. How high does the ladder touch the wall from the ground?
(b) if ![]() where
where ![]() is an acute angle. Find
is an acute angle. Find
10. (a) In a primary school of 150 pupils, 50 study hisabati, 70 study sayansi and 40 study both subjects. By using a venn diagram find the number of students who study neither hisabati nor sayansi.
- The score of mathematics test done by 50 form two students in a certain school are shown in the table below.
| Marks(%) | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| No of students | 6 | x +3 | 2x + 3 | x - 2 | 9 | 4 | 5 | 2 |
- Find the value of
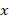
- Calculate the number of students who passed the examination, if the pass mark was 50%.
- Which mark was scored by many students?
FORM TWO MATHEMATICS EXAM SERIES 49
FORM TWO MATHEMATICS EXAM SERIES 49
THE PRESIDENT’S OFFICE
REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
MOSHI MUNICIPAL COUNCIL
SECONDARY EDUCATION EXAMINATIONS SYNDICATE
041 BASIC MATHEMATICS
FORM TWO MOCK EXAMINATION
Wednesday 29thJune 2022 Am Time: 2:30 Hour
INSTRUCTIONS
- This paper consists of ten (10) compulsory questions.
- Show clearly all the working and answers in the space provided.
- All writing must be in blue or black ink except drawing which must be in pencil.
- Write your number at the top right corner of every page
1. (a) Equal squares as large as possible are drawn on a rectangular board measuring 54cm by 78cm. Find the largest size of the squares.
(b) (i) Express 2.7?9? as a fraction in the form a/b where a and b are integers and b≠0
(ii)Arrange 2/5, 5/8 ,48% and 0.6 in ascending order
(iii) Show on the number line the solution set of the inequality
?2x+1?>3
2. (a) write 624.3278 correct to :
(i) Five significant figures
(ii) Three decimal places
(b) i. A rope of 18m and 80cm is to divided into four equal parts . How long will each part be? (Give your answer in meters and centimeters).
ii. 50% of the contents in a box weigh 8kg 40gm. What does the whole content weigh?
3. (a) Rectangular table top is 2m long. If the area of the rectangular table top is
3.96m2. find its width
(b) i. Solve the following simultaneous equations
2x+3y=5
4x+23=5y
ii. If Fatuma is 4 years less than Bakari and 3 times Fatuma's age is equal to 2 times Bakari's age. What are their ages ?
4. (a) i. If x2 +ax +4=0 is a perfect square . Find the value of a
ii. If x2 +bx +c =(x-3)(x+2) determine the values of b and c
iii. Solve the following quadratic equation by complete the square method x2 + 6x +7=0
(b) i. Solve 3 - ![]() of (6x+9) = 5-2x
of (6x+9) = 5-2x
ii. If U*V =UV+V, Find x given that (x*2)*5=60
5. (i) John, Ramadhani , Marry and Sam have 600 ,100, 500 and 300 shares in a cooperative shop respectively. Divide 150,000 shs among them in the ratio of their shares.
(ii) A real estate agent received a 6% discount on the selling price of a house . If the discount was Tsh.888,000. What was the selling price of the house ?
6. (a) i. A straight line passes through two points A(-3,6) and B (-6,3).
Find the gradient of the straight line AB.
ii. Find the Y- intercept of the line joining points (5,3) and (3,2). (b) i. The transformation T maps the point (x,y)(x-y,x). Find the image of the point (6,-2).
ii. Find the image of a point P(3,2) after rotating it about the origin through 900 in a clockwise direction.
iii.What is the centre of an enlargement given that the image of A(3,2) under the enlargement scale factor 2 is A'(6,4).
7. (a) (i) Solve for X if ![]()
(ii) Given that
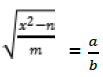
make x as the subject of the formula.
(iii) Express
![]()
in the form a + b√c
(b) (i) If log 2=0.30103 and log 3 = 0.47712 evaluate log 48.
(ii) Use mathematical tables to evaluate the following mathematical expression,
![]()
8. (a) In the figure below, EH = GH and both ΔEHF and ΔGHF are right – angled triangles. Prove that ΔEHF and ΔGHF are congruent
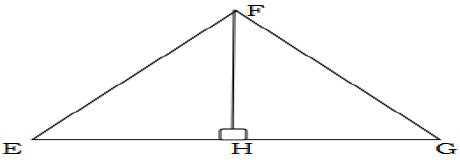
(b) If ΔPQR ∼ ΔLMN and lengths PR = 20cm, NL = 10cm, NM = 12cm and LM = 9cm, find the length of the other sides of ΔPQR
9. a) In a right – angled triangle, tan θ = ![]() . Find the value of
. Find the value of
iSin θ
ii 2Cos θ
(b) A ladder 15m long, rests against a vertical wall such that the foot of the ladder is 6m from the wall of a horizontal floor. Find
(i) the angle that the ladder makes with the wall
(ii) the height above the floor at the point where the ladder touches the wall
10. (a) (i) Given that n(A) = X, n(B) = X + 4, n(An B) = 3 and n(Au B) = 17 where A and B are joint sets. Find the value of X
. (ii) In a class of 42 students 31 students study History and 26 students study Physics. Using Venn diagram, find the number of students who study Physics only.
(b) The scores of mathematics examination done by 50 form two students in a certain school are shown in the table below
| Marks (%) | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| Number of students | 6 | x+3 | 2x+3 | x-2 | 9 | 4 | 5 | 2 |
(i) Find the value of x
(ii) Calculate the number of students who passed the examination if the pass mark was 50%.
(iii) What was the score obtained by majority of the students?
FORM TWO MATHEMATICS EXAM SERIES 28
FORM TWO MATHEMATICS EXAM SERIES 28
PRESIDENT'S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
TANZANIA HEADS OF ISLAMIC SCHOOLS COUNCIL
FORM TWO INTER ISLAMIC MOCK EXAMINATION
041 BASIC MATHEMATICS
TIME: 2:30 HOURS Thursday, 23rd September 2021 a.m.
Instructions
1. This paper consists of ten (10) compulsory questions.
2. Answer ALL questions
3. Each question carries ten (10) marks.
4. Show clearly all the workings and answers in the spaces provided.
5. All writings must be in blue or black ink except for drawings which must be in pencil.
6. Four figures/mathematical tables, geometric instruments and graph papers may be used where necessary.
7. Calculators, cellular phones and any unauthorized materials are not allowed in the examination room.
8. Write Your Examination Number at the top right corner of every page.
| FOR EXAMINER’S USE ONLY | ||
| QUESTION NUMBER | SCORE | EXAMINER’S INITIALS |
| 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
| 5 | | |
| 6 | | |
| 7 | | |
| 8 | | |
| 9 | | |
| 10 | | |
| TOTAL | | |
| CHECKER’S INITIALS | | |
1. (a) Three bells ring at intervals of 20 minutes, 30 minutes and 40 minutes. If they start ringing together at 7.30 am
(i) After how long will they ring together again?
(ii) At what time will this be?
(b) Round off 349.678 to the nearest.
(i) Tens
(ii) Hundredth
(iii) One significant figure
2. (a) Write ![]() in form of
in form of ![]() , where b ≠0.
, where b ≠0.
(b) In a class of 40 students ![]() are boys. Two fifth of the girls wear spectacles.
are boys. Two fifth of the girls wear spectacles.
How many girls do not wear spectacles?
3.(a) Perform
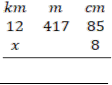
(b) Find the time in which sh 200,000/= will earn sh 48,000/= at the rate of 4% interest per annum.
4. (a) Calculate the angles marked with letters X, Y and Z.
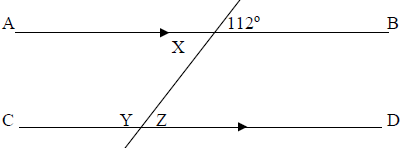
(b) Find the area of rectangle whose perimeter is 30cm and its length and width are (3W-7) cm and (W+2) cm respectively.
5. (a) Factorize the expression 6x2 – 11x + 4 by splitting the middle term.
(b) The sum and difference of the two numbers are 9 and 3 respectively. Find the possible numbers.
6. (a) (i) Find the equation of the straight line passing through (3,5) and (7,9).
(ii) Calculate the gradient and coordinates of the y-intercept of 2x+3y=12.
(b) Find the image of a point (-4, 3) after a reflection on y-axis followed by another reflection on y=0.
7. (a) If
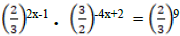
Find the value of X.
(b) Rationalize ![]() writing the answer in the form a
writing the answer in the form a![]() where a, b, c and d are real.
where a, b, c and d are real.
(c) Given log2 = 0.3010, log3 = 0.4770 and log7 = 0.8451. Find the value of log294.
8. (a) Calculate the length of EC and CD in figure below:
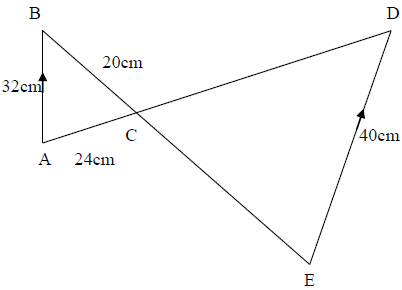
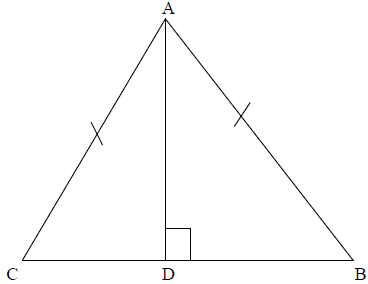
(b) Use the figure below to prove that triangle ADB ≡ Triangle ADC
9. (a) A rectangle has sides of 12mm and 16mm. Calculate the length of one of its diagonals.
(b) Calculate the exact value of ![]() .
.
10. (a) In the Venn diagram below:
U = { Boys in form II at a certain secondary school}
F = { Members in the football team}
B={ Members in basketball}
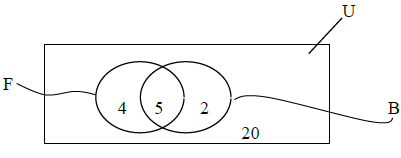
(i) How many boys are in the football team?
(ii) How many boys are in both teams?
(iii) How many are in the football team but not in the basketball team?
(iv) How many are neither basketball nor football team?
(v) How many boys in form II at the school?
10. (b) The table below shows the distribution of the score of 60 students in Mathematics table at MJI MWEMA secondary school.
| Marks % | 45 – 55 | 56 – 66 | 67 – 77 | 78 – 88 | 89 - 99 |
| No. of students | 11 | 15 | X | 17 | 10 |
(i) Find the value of X.
(ii) Find the percentages of the student score ate most 77 marks.
FORM TWO MATHEMATICS EXAM SERIES 11
FORM TWO MATHEMATICS EXAM SERIES 11
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256