THE UNITED REPUBLIC OF TANZANIA PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
GAIRO DISTRICT COUNCIL
FORM FOUR PRE – MOCK EXAMINATION
041 BASIC MATHEMATICS
19Th March 2024 Time 3:00 Hrs - A.M
Instructions
- This paper will consist of sections A and B with a total of 14 questions
- Answer all questions in both sections A and B
- Section A will carry 60 marks and section B will carry 40 marks
- Mathematical tables/ Calculator may be used
- Write your Examination number on the top right corner of your answer booklet provided. Use R = 6400 and π= 3.14
SECTION A (60 MARKS)
1. (a) Write a number in which O represents hundreds, 7 represents ten thousands, 3 represents ones, 9 represents thousands, 6 represents hundred thousand and 8 represents tens.
(b) Convert ![]() and 360% to decimal, then approximate their products to one significant figure.
and 360% to decimal, then approximate their products to one significant figure.
(c) 14 - [−2 − (8 ÷ 2) + 5]
2. (a) If log 2 = 0.3010, Find the value of log 5 , without using mathematical table
(b)If (3x+1)(22y+9) = 69984 find the values of x and y.
(c)Simplify by rationalizing the denominator of
![]()
3. (a) A bag contains 5 red and 4 blue balls. Two balls are drawn in succession without replacement. Find the probability that both are red.
(b) In a class of 35 students, 19 take physics, 18 take History and 3 take neither of the two subjects. Calculate how many students take
i) Both subjects ii) Physics or History
4. (a) Find the equation of a line passes through the point of intersection of the lines 3x -2y -8=0 and 2x+y =3 and is perpendicular to line 4x +3y=0
(b) If a =3j – i and b=5i-2j and c = 4a + 3b find
(i). Magnitude of ç
(ii). Direction of ç
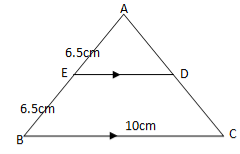
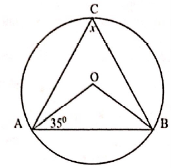
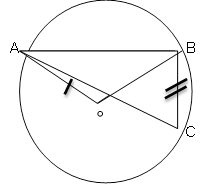
5. (a) The area of the triangle ABC is 140 cm2 ,side AB = 20 cm, AC is 14 cm. Find the angle BAC
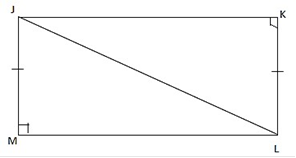
(b) (i) From the Rectangle JKLM given below (i) name two triangles which are congruent.
(ii) Prove your answer in (i) above
6. a) Given that (Z + 1) is directly proportional to x and inversely proportional to the square root of y. If x =2 when y=4 and Z =4 find Z when X = 3 and y =9
(b) A bus travels 240 km using 16 litres of diesel. How many liters of diesel are needed to drive 90km?
7. (a) On January 1st 2015 MTL group started a business with a capital in cash of 2,000,000/=
- January 2. Purchased goods for cash 1,400,000/=
- 3. Sold good for cash 1,000,000/=
- 6. Purchased goods for cash 60,000/=
- 15. Paid rent for cash 220,000/=
- 26. Sold goods for cash 620,000/=
Prepare the cash account and balance it
(b) If the ratio of sacks of maize, millet and cassava in certain store is 6:7:3. There are 42 sacks of millet. Find the total sacks in a store.
8. (a) If the common difference of an A. P is -2 and the third term is 0. Find (i). The first term (ii). The general term
(b) A certain geometric progression has a common ratio of 2 and the sum of the first ten terms is 155. Find the first term and give the formula for the nth term
9. (a) Without using tables, find the value of  and simplify your answer.
and simplify your answer.
(b)The sides of a right angled Triangle are (2x + 1)Cm, (12x)Cm and (12x + 1)Cm. Find the value of x in cm if the hypotenuse is (12x + 1)cm
10. (a) Use factorization method to find the value of x if 8x2 – 34x + 21 = 0
(b) The average of two numbers is 7 and three times the difference between them is 18. Find the two numbers
SECTION B (40 MARKS)
11. (a) These scores of Mathematics Examination done by 60 students were recover as follow
36, 26, 52, 54, 51, 34, 26, 29, 34, 26, 30, 56, 21, 49, 35, 58, 22, 38, 28, 26, 41, 53, 31, 32, 20, 21, 61, 58, 36, 50, 56, 63, 27, 30, 63, 30, 60, 34, 48, 28, 41, 57, 24, 35, 35, 33, 20, 59, 36, 25, 32, 43, 56, 30, 50, 42, 21, 33, 45, 25
i) Prepare frequency distribution table using intervals 20- 24,25 -29, 30-34 ii) Calculate mode and Median
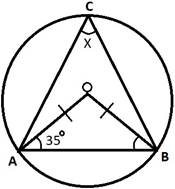
(b)Find the value of angle x, in the figure below
12. (a) The figure below shows a rectangular prism in which AB= 10CM, BC= 8cm and GC = 6cm
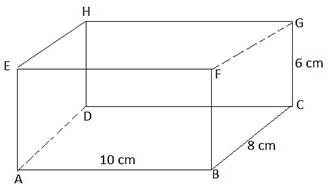
(i). Calculate the length AG (Two decimal places)
(ii). The angle that AG makes with the plane ABCD
(b) A and B are two points on latitude 70°N. Their longitudes are 62°W and 118°E respectively. Calculate the distance in Kilometers from A to B if the Earth’s diameter is 12,800km along a parallel of latitude
13. (a) Think of two numbers. If I double the first and add the second I get 18. If I double the first and subtract the second I get 14. Use matrix method to find the two numbers
(b) Find the value of “t” given that 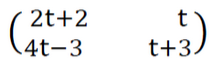 is a singular matrix.
is a singular matrix.
(c) Find the image equation of the line y = 3x + 7 after reflection is the line y=x
14. (a) Maximize f(x, y) = 2x + 6y subject to the following constraints
x + y ≤ 7
2x + y ≤ 12
x + 3y ≤ 15
x ≥ 0 y ≥ 0
(b) The function f(x) defined as:-

(i) Sketch the graph of f(x)
(ii) State domain and range of f(x)
FORM FOUR MATHEMATICS EXAM SERIES 227
FORM FOUR MATHEMATICS EXAM SERIES 227
THE UNITED REPUBLIC OF TANZANIA PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
ZONAL FORM FOUR MOCK EXAMINATIONS
(NJOMBE, MBEYA, SONGWE, RUKWA AND KATAVI REGIONS)
041 BASIC MATHEMATICS
TIME 3:00 HRS YEAR -2023
INSTRUCTIONS
- This paper consists of section A and B with a total of fourteen (14) questions.
- Answer ALL questions in sections A and section B.
- Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly in answer booklet provided.
- NECTA Mathematical tables and calculators may be used.
- Smart watch and cellular phons are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s)
SECTION A: (60 Marks)
Answer all questions in this section.
1. (a) Given the number 85763.6721 , write this number;
(i) To nearest thousands
(ii) To hundredth
(iii) In expanded form
(b) Three brothers visited the grandfather at an interval of 5days, 7 days and 12days. If they started together at 15th July. Find the date they will visit the grandfather to gether next time (Each month contains 30 days).
2. (a) (i) Solve for x if
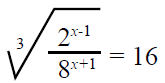
(ii) Simplify the following by rationalizing the denominator of
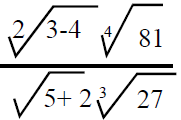
(b) Given that log34=1.262 and log35 = 1.1465. Find log3 0.8
3. (a) Given that A = and B = { x 0 ≤ x ≤ 8}, { x ≤ 3 where x ≤ 11}, x is an integer. Represent each of the following by using Venn diagram.
(i) A ∩ B
(ii) ) A ∪ B
(b) Each letter of the word PROBABILITY is written on separate card and the cards were shuffled. If a card with the latters is picked at random,what is the probability that it is;
(i) A vowel
(ii) A consonant
4. (a) Four consecutive vertices of a parallelogramare at A (-1,2), B(5,1), C(6,5) and D (x,y) V find the coordinate of the vertex D.
(b) Give the vectors a = i + 3j, b = 5i - 2j and c = 4a + 3b. find:
(i) Magnitude of vector c
(ii) Find the unit vector d where by d =2a - 3b +c
5. (a) A certain regular polygon is inscribed in a circle of radius 3cm , if the length of a side of a polygon is 3cm. Find:
(i) Number of sides of a regular polygon.
(ii) Draw the diagram of the polygon.
(iii) What is the name of the polygon drawn in part (a)(ii) above.
(b) The dimensions of the first rectangle are length 23cm and width 16cm , a second rectangle has length 12 cm and width of 9cm . With reason(s) state whether the two rectangles are similar.
6. (a) A school cow produces 18 litres of milk every day. How many cows of the same type should the school keep to get 126 litres of milk every day?
(b) One family from England traveled for holiday to France and exchanged 450 pounds for euros when the exchange rate was 1.41 euros to the pound. They spent 500 euros and then exchanged the remaining amount into pounds by that time the exchange rate had become 1.46 euros to the pound. How much money remained in terms of pounds?
7. (a) (i) In a certain class, the ratio of boys and girls is 5.3 . On a certain day only 3/5 of the students were present while 16 students were absent on that day. Find the number of students in a particular class.
(ii) A radio is sold at Tsh 40,500/=. Price, this price includes 20% Value Added Tax (V.A.T). Calculate the amount of V.A.T.
(b) Assume that you are a business man with the following transactions.
| Opening stock at 1st January, 2021 | Tsh. 34,500/= |
| Closing stock at 31st December, 2021 | Tsh. 26,700/= |
| Net Purchases in a year | Tsh. 219, 300/= |
| Gross profit made in a year | Tsh. 138,550/= |
| Expenses for the year | Tsh. 45,800/= |
Use the above information to find the cost of goods sold.
8. (a) A school hall has 32 rows of seats. If there are 26 seats in the first row, 30 seats in 2nd row, 34 seats in 3rd row and so on. How many seats are there in a theater?
(b) Mr. Cuthbert starts an employment with a monthly salary of Tsh. 340,000/= and receives an increment of Tsh. 12,000/= every year.
(i) What will be his salary in the fourteenth year of employment?
(ii) After how long would he be earning Tsh. 592,000/= per month?
9. (a) If 5tanθ =12 , evaluate
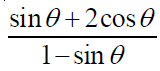
(b) A rectangular frame ABCD measured 48cm by 55cm is made from wire. The diagonals of the frame are also made from wire. Calculate the length of the wire used to make the frame and diagonals.
10. (a) Solve for in X in - 1≤ 3x − 2 < 8
(b) By using completing the square method, solve the equation
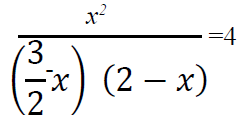
SECTION B: (40 Marks)
Answer all questions in this section.
11. (a) The number of patients who attended maternity clinic daily in June 2008 in a certain village was recorded as follows;
| 52 61 42 27 38 44 56 36 73 22 41 48 77 30 46 43 72 63 43 76 47 53 38 55 60 51 47 58 33 37 |
(i) Make a frequency distribution table by grouping the number of patients in class intervals 20- 29, 30 - 39, 40 - 49, ...
(ii) Calculate the mean if the assumed mean is 44.5
(iii) Construct a pie chart for the frequency distribution in (a)(i) above.
(b) In the figure below, find the size of the angle marked with letter x and y.
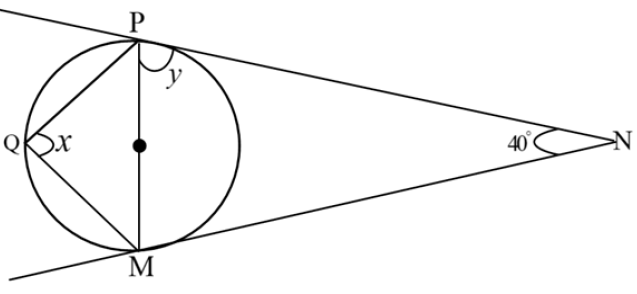
12. (a) A circular tank has a base of 53m radius and height of12m . If the tank is half full of water, what is the volume of water in a tank? Give your answer in litres ( 1m3 =1000litre ).
(b) A ship sails from Pemba (50S, 390E ) to Dar es Salaam (80S, 390E). If it leaves Pemba at 11.30am and arrived in Dar es Salaam at 01.30pm . With the aid of diagram find the speed of the ship in . km h/
13. (a) The matrix
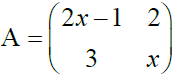 has no inverse. Find the value(s)of x
has no inverse. Find the value(s)of x![]()
(b) Find the possible value of x given that
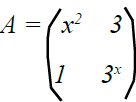 and
and
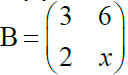
if AB = BA
(c) A linear transformation T maps (x, y) onto (x' , y'), such that
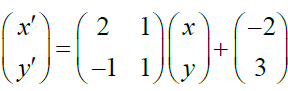
(i) Find the image of (2,-3) under T.
(ii) If (3,1) is the image of B ( m,n) under T above find the values of m and n
(iii) Find T if (u) if u = (3,5)
14. (a) The function f is defined by f x: → ax2 + b for x ∈ R whereby a and b are constants. It is given
that f(2)= 1 and f(5)= 8 .
(i) Find the value of a and b
(ii) Solve the equation f (x) = 0
(b) A COCA-COLA company makes two types of drinks, Fanta and Coca-cola. The two drinks are very similar and the same equipments can be used either. In making of Fanta one man can supervise 10 machines and the batch will give the profit of Tsh. 100,000/= per week and Coca-cola yields Tsh. 500,000/= of profit per week by using 25 machines and 8 men. If there are 200 machines and 40 men available, how many batches of Fanta and Coca-cola should be produced to maximize profit?
FORM FOUR MATHEMATICS EXAM SERIES 190
FORM FOUR MATHEMATICS EXAM SERIES 190
 | THE UNITED REPUBLIC OF TANZANIA MBEYA CITY COUNCIL ACADEMIC COMMITTEE FORM FOUR PRE-MOCK II EXAMINATION |  |
CODE: 041 BASIC MATHEMATICS
Time: 03:00 HRS Monday, 15th May 2023 a.m.
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in both sections.
- Each question in section A carries 06 marks and each question in section B carries 10 marks.
- All necessary working and answers for each question should be shown clearly.
- NECTA mathematical tables and non-programmable calculators may be used.
| FOR EXAMINER’S USE ONLY | ||
| QUESTION NUMBER | ||
| SCORE | EXAMINERS INITIALS | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| TOTAL | ||
SECTION A (60 MARKS)
1. (a) A girl walked 432 paces, a boy walked 648 paces and a woman walked 540 paces from the same home to the market. If they started at the same time and used the same speed, how many times did they step together.
(b) Write 699.6789 correct to
(i) three significant figures
(ii) three decimal places
2. (a) Express (7 + √2)2 in the form of a + b√c
(b) Find the value of x given that 2logx = log4 + log (2x − 3)
(c) Solve for y given that 125y+1 + 53y = 630
3. (a) In a class of 60 students, 40 students like History, 36 students like Geography, 24 students like both subjects. Find the number of students who like;
(i) history only (ii) geography only
(iii) either history or geography (iv) neither history nor geography (b) When a fair die is tossed, find the probability that the number obtained is,
(i) more than five (ii) at least one (iii) at most six.
4. (a) If a = 5i + 4j, b = −3i + 3j and c = −2i + 5j
Find (i) v = 2a + b − 3c (ii) the magnitude of v
(b) Given the points A (3, 3), B (-3, 1), C (-1, -1) and D (1, -7).
(i) show that the line through AB and CD are perpendicular to each other.
(ii) find the equation of the line through the point (-4, 5) which is parallel to BC.
5. (a) Prove that the exterior angle of a cyclic quadrilateral is equal to the opposite interior angle. (b) The area of the regular polygon inscribed in a circle is 2268 cm2. If the polygon has 9 sides, find the,
(i) perimeter of the circle (ii) perimeter of the polygon
6. (a) Mwamwenda received Kshs 1,000,000 from his brother in Kenya. How much did he get inTanzanian currency (Tshs) if one Kenyan shilling was equivalent to 12.5 Tanzanian shilling?
(b) The energy (E) stored in an elastic band varies as the square of the extension (![]() ). When the elastic band is extended by 4 cm, the energy stored is 240 joules. What is the energy stored when the extension is 6 cm? What is the extension when the stored energy is 60 joules?
). When the elastic band is extended by 4 cm, the energy stored is 240 joules. What is the energy stored when the extension is 6 cm? What is the extension when the stored energy is 60 joules?
7. (a) Three businessmen shared Tshs 280,000 so that the first one got twice as much as the second, and the second got twice as much as the third. How much money did each businessman get?
(b) Prepare a trial balance using the following information so as to get the starting capital of business as at 31st December,2020.
- Creditors . . . . .. 750000Tsh
- Equipment . . . .... 540000Tsh
- Cash in hand . . . . 12000Tsh
- Debtors . . . . . . 94000Tsh
- Premises . . . . .. 400000Tsh
- Bank loan . . . . . 150000Tsh
8. (a) The fifth and eleventh terms of an arithmetic progressions are 8 and -34 respectively. Find the sum of the first ten terms.
(b) A school wishes to invest Tshs 100,000,000 in a bank which pays an interest rate of 2% compounded annually.
(i) find the total amount of money that will be accumulated after two years.
(ii) calculate the interest after two years.
9. (a) The following diagram shows the location of three houses, A, B and C. how far is house C from house B?
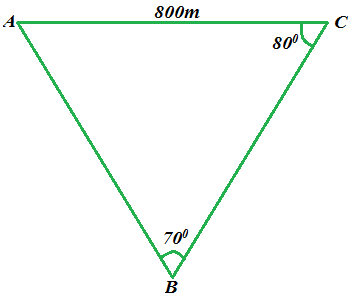
NOTE: angle ABC = 700, angle ACB = 800 and length AC = 800m
(b) A rectangular frame is made of wooden bars. The diagonal of the frame is 25 cm long and its width is 15 cm. find the length of the frame.
10. (a) Asha is three years older than her brother Juma. Three years to come the product of their ages will be 130 years.
(i) formulate the quadratic equation representing the information above.
(ii) use the quadratic formula to find the present age of Asha and Juma.
(b) Solve the equation by completing the square. 2x2 − 3x − 5 = 0
SECTION B (40 MARKS)
11.The following are the marks obtained by 40 students in a mathematics test.
47 44 58 48 47 57 56 71 62 46 45 50 76 73 43 54 58 66 48 32 89 60 42 47 54 67 35 54 52 44 64 49 37 64 67 44 45 45 42 34
(a) Use the following information to prepare the frequency distribution table.
-Number of classes = 6
-Size of each class = 10
-The lower limit of the first class interval = 32
(b) use the frequency distribution table prepared above to find to find the actual mean when the assumed mean is 86.5.
(c) calculate the difference between the actual mean and the median of this distribution.
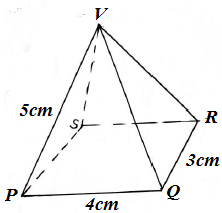
12. A rectangular base pyramid VPQRS below is such that VP=VQ=VR=VS=5cm, PQ=4cm and QP= 3cm.
Find (a) (i) the projection of VP on PQRS
(ii) the angle between the VP and PQRS.
(b) A boat sails from Unguja (4.50S, 39.50E) to Dar es Salaam (7.50S, 39.50E). If it leaves Unguja at 11.30 a.m and arrived in Dar es Salaam at 13.30 p.m, find the speed of the boat in km/h. use pie = 22/7 and the radius of the earth 6370km.
13. (a) find the value of a, b, c and d in the following matrix equation.
![]()
(b)find the image of the point (5,-4) after a reflection in the line y = -x followed by another reflection in the line x = 0.
(c) A translation takes the point (4, 4) to the point (-6, -6). If it takes (x, y) to (-3,-3), find the value of x and y respectively.
14. (a) A function is defined by
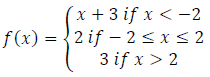
(i) Sketch the graph of f(x)
(ii) From the graph determine the domain and range
(iii) Find the value of f(5) and f(-3).
(b) A small book shelf cannot have more than fourteen books. At least four should be fiction books and more than six of the books should be non-fiction. Formulate the inequalities to represent this information.
FORM FOUR MATHEMATICS EXAM SERIES 165
FORM FOUR MATHEMATICS EXAM SERIES 165
THE UNITED REPUBLIC OF TANZANIA PRESIDENT'S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
DODOMA REGION
FORM FOUR MOCK EXAMINATION-2023
041 BASIC MATHEMATICS
Time: 3 Hours August, 2023
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in BOTH sections A and B
- Each question in section A carries six (06) marks while each question in section B caries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- Mathematical tables and non-programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer sheet(s).
SECTION A (60 Marks)
Answer all questions in this section
1. (a) Rajabu is making small metal rods. He has three pieces of metals of the length 432cm, 648cm and 540cm. What is the longest length of the rod he can make if the rods have the same length and no metal is wasted”
(b) A wire length 80cm is cut from the right side 10% and from left side 30% of its length at the same time. Find the remaining length of the wire.
2. (a) Find:
(i) The value of log 900 given that log3 = 0.4771
(ii) The value of logba, if log9aa = log27b.
(b) Solve for x if (4xx+3)(16xx) = (83xx)
3. (a) In a school of 75 pupils, 40% of pupils take Biology but not chemistry, 32% take both subjects and 12% of them take chemistry but not Biology.
(i) Display this information on Venn-diagram
(ii) How many pupils do not take either Biology or Chemistry
(b) If a number is chosen at random from integers {1,2,3 …..12}; find the probability that:
(i) It is divisible by 3
(ii) It is greater than 4 and less than 12
4. (a) The coordinates of point A, B and C are (4, 3) , (3, -2 ) and (7, -1) respectively .Find:
(i) Length AB
(ii) Equation of line perpendicular bisector to a line BC give your answer in the form of y = mx + c
(b) If a = i +2j, b = i- 2j and c = 5i+14j. Calculate:
(i) Unit vector in the direction of vector v= 3b – a + c
(ii) Direction cosines of vector v
5. (a) In the figure below AB= 3cm, < BCA = 300 and <BDC = 90. Given that <ABC =<BDC
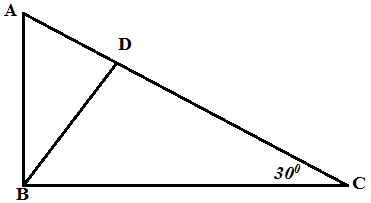
(i) Prove that ?BDC ~ ? ABC
(ii) Calculate length BD
(b) Two concentric regular Hexagons are such that the radius of circle inscribing the larger on is twice that inscribing the smaller hexagon. If the radius of smaller is 5cm. find area between the two Hexagons.
6. (a) The value of “V” of a diamond is proportional to the square of its weight “W”. It is known that a Diamond weighing 10grams is worth Tsh 200,000/=
(i) Write down expression that relates V and W
(ii) Find the weight of a diamond that worth Tsh 5,000,000/= (b) A day worker is paid Tsh 48,000/= for 16 hours work.
(i) What is the rate of payment?
(ii) At this rate, how much would he receive for 30 hours of work?
(iii) At this rate, for how long must he work in order to receive Tsh 120,000/=
7. The following information refers to MR Kajasho’s trade as is at 31th October 2022
Sales ……………………………………………………………400,000/=
Gross profit ……………………………………………………..25% of sales
Opening stock ………………………………………………….. 20% of cost of sales
Expenses ……………………………………………………….. 10% of gross profit
Closing stock …………………………………………………… 120,000/=
Calculate;
(a) Opening stock
(b) Cost of sales
(c) Purchases
(d) Net profit
(e) Expenses
8. (a) Show that ![]()
(b) Find by how much the compound interest exceeds the simple interest on 8000/= for 2 years at 8% interest rate per annum.
9. (a) The Hypotenuse of an isosceles right-angled triangle is 8cm. Is there enough information to find the lengths of adjacent sides?. If so, find their lengths. If not, explain why not.
(b) If cos ( x − 30) = − 0.5. What are the values of x for 00 ≤ x ≤ 3600
10. (a) Twice the length of rectangle exceeds three times the width of rectangle by one centimeter. If one third of the difference of the length and the width is one centimeter, find the dimensions of the rectangle.
(b) A piece of a copper wire which is 56cm long is bent to form a rectangle of area 171cm2. Find the dimensions of rectangle formed.
SECTIONB (40 Marks)
Answer all questions in this section.
11. (a) The following scores obtained by 22 students as follows
49,64,38,60,46,74,68,42,38,68,57,63,76,51,54,66,62,63,58,59,47,35
i. Prepare frequency distribution table with class size 5 and take the lower mark to be 35
ii. Estimate mode from Histogram
iii. Calculate median
(b) Prove that if one side of cyclic quadrilateral is produced, the exterior angle formed is equal to interior opposite angle.
12. (a) A plane starts at ( 200S, 300E ) and flies north for 4000km. find its new location
(b) A rectangular prism with top PQRS and Base ABCD has AB=12cm, BC=5cm, and RC=4cm
Calculate:
(i) AR
(ii) The angle that AR makes with base ABCD
(iii) Total surface area
13. (a) If matrix
A=![]()
Find value of matrix B such that AB=C
(b)A straight line whose equation is m = 5 − 6y meets another straight line whose equation is ![]() x –y =0 at point “P”. Find the value of coordinate P by inverse method.
x –y =0 at point “P”. Find the value of coordinate P by inverse method.
14. (a) Two printers N and T produce three different types of books. N produce 80 type I books per day, 10 type II books per day and 20 type III books per day. T produces 20 type I books per day, 10 type II books per day and 70 type III books per day. The orders placed are 1600 type I books, 500 type II books and 2100 type III books. The daily operating cost for N is Tsh.10, 000 and for T is Tsh.20, 000. How many days should each printer operate to meet the orders at a minimum cost?
(b)Plot the graph of y = 2m2 for −2 ≤ m ≤ 4 and use it to solve the equation:
2x2-3x-2=0
FORM FOUR MATHEMATICS EXAM SERIES 155
FORM FOUR MATHEMATICS EXAM SERIES 155
PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
LINDI REGIONAL
FORM FOUR MOCK EXAMINATION
041 BASIC MATHEMATICS
TIME: 3:00HOURS MAY 2023 .
Instructions
- This paper consists of section A and B with a total of 14 questions
- Answer all Questions
- Each question in section A carries six (06) Marks while each question in section B carries ten (10) Marks
- All necessary working and Answers for each question must be shown clearly.
- NECTA mathematical tables and non-programmable calculators may be used.
- All communications devices and any Unauthorized material are not allowed in the examinations
- Write your examination number on every page of your answer sheets
SECTION A (60 Marks)
Answer all questions in this section
1. (a) Find the approximate value of the expression by rounding off each number in the
Expression![]() to one significant figure
to one significant figure
(b) Square tiles are used to build a floor measuring 12metres by 16metres. If the tiles
are of different sizes and only whole ones are used.
(i) What is the largest size of the tiles?
(ii). How many tiles used to cover the whole floor
2. (a) Given that, ![]() = 1.2 without using tables find the value of
= 1.2 without using tables find the value of
![]()
(b) Solve for x if ![]()
3. Kilabela secondary school. 40 students were asked about whether they like
Volleyball or Netball or Both. It was found that the number of students who like
Both Volleyball and Netball was three times the number of students who like
Volleyball only. Furthermore, the number of students who like Netball only was 6 More than twice the number of students who like Volleyball only. However 4 Students like neither Volleyball nor Netball
(a) Represent this information in a Venn diagram letting y be the number of students who like Volleyball only?
(b) Use the results obtained in part (a) to determine the probability that a student selected at random likes;
(i) Volleyball only
(ii) Both volleyball and Netball
4. (a) (i) Find the equation of aline passing through point (2, 4) and the midpoint of (0, 6) and (10, 12). Write
your answer in form of ax+by+c=0.
(ii) If the line from the point (−4, y1) to the point (x2, −3)is bisected at the point (1, 1). Find the values of y1 and x2
![]() (b) Determine whether the triangle with vertices O (0, 0), A (-6, 8) and B (-14, 2) is Equilateral, Isosceles, Scalene
(b) Determine whether the triangle with vertices O (0, 0), A (-6, 8) and B (-14, 2) is Equilateral, Isosceles, Scalene
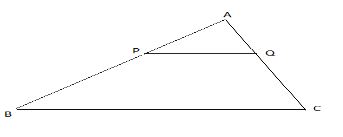
5. In the figure below![]() ,
, ![]() ,
,![]() and
and ![]() and the area of
and the area of ![]() .
.
(a) Show that ![]() is similar to
is similar to ![]()
(b) Calculate the length of ![]()
(c) Find the area of ![]()
6. (a) A students had two plant seedlings. She measured the rate at which the seedlings were growing.
Seedling A grew 5 cm in 10 days and seedling B grew 8 cm in 12 days.
Which seedling was growing more quickly?
(b)Suppose x varies directly as y square andinversely as p. if x=2, when y=3 and p=1, Find the value of y when x=4 and p=5.
7. (a) Kijuguu got a profit of 20% when sold a Radio for Tshs 122400. What would be her percentage loss if she sale a radio for Tsh 76500?
(b)Given that the following transactions.
- Sales for 2019--------- 51,000tshs
- Stock at start ------------9,000tshs
- Purchases ---------------34,650tshs
- Stock at close -----------6,000tshs
- Return on sales ---------1,000tshs
- Return on purchase -----150tshs
- From the transaction deduce.
- Cost of goods for sale
- Average stock
- Net sales (turn over)
8. (a) Kabujage Saved Tshs 6 million in a savings Bank whose interest rate was 100% compounded annually.
Find the amount in Kabujages’s savings accounts after 5 years
(b) A small business sells products with 1,000,000tshs during its first year. The owner of the business has
set a goal of increasing annual sales by Tshs 750,000 each year. Assuming this goal is met. Find the total sales during the first 10 years of the business in operation
9. (a) A rope of length 39m is tied to the top of a flag pole. The other end of a rope is fixed at a point 36m from the base of the flag pole. How high is the flag pole?
(b) A student 1.6m tall and standing 52m from the foot of tree sees a bird on top of the tree
If the angle of elevation of the bird from his eye is![]() , find the height of the tree.
, find the height of the tree.
10. (a) Use completing the square to solve the quadratic equation x2 + 18x +28 = 0
(b) When 6 is divided by a certain number, the result is the same as when 5 is added to the number and that sum divided by 6. Find the number.
SECTION B: (40 MARKS)
11. (a). The frequency distribution table below shows the distribution of 100 families according to their expenditure per week.
| Expenditure | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Number of families | 14 | X | 27 | Y | 15 |
(i) Calculate the missing frequencies if the mode is 24.
(ii) The median
(iii) Find mean by using assumed mean=25
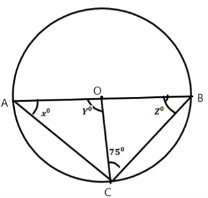
(b). (AB) is a diameter of circle .If ![]() OCB=75°, find the values of x, y and z
OCB=75°, find the values of x, y and z
12. (a) A speed boat travelling from Mwanza (3° S, 33° E) to Mara (1° S, 33° E) using 30 knots left Mwanza at 11:30 a.m. At what time did it reach Mara?
(b) A right rectangular pyramid has sides of the base 6cm by 8cm and slant height 13cm, now;
(i) Sketch the right pyramid showing the above information.
(ii) Determine the height of the pyramid
(iii) Determine the angle between the base and the slant edge.
(iv) Determine the volume of the pyramid
13. (a) One pair of opposite sides of a parallelogram is (4x+y) units and (3x+5) units while the other pair is (2x-y)units and 4 units. Find the value of x and y
(b) Find the image of the value of point (x, y) obtained from (a) above when it is first rotated through ![]() about the origin and then followed by reflection about the line y+x=0
about the origin and then followed by reflection about the line y+x=0
14 (a) Given![]() . Find
. Find ![]()
(b) The graph belowrepresents a relation ![]()
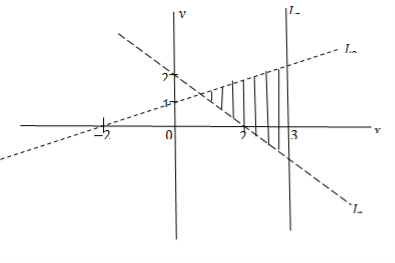
- Find the relation

- State the domain and range of the relation
 from the graph
from the graph
(c)A function f is defined
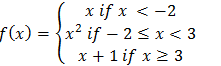
(i) Sketch the graph of ![]()
ii) Use the graph to determine the domain and range of f(x).
FORM FOUR MATHEMATICS EXAM SERIES 148
FORM FOUR MATHEMATICS EXAM SERIES 148
 | PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT MVOMERO DISTRICT COUNCIL |  |
FORM FOUR MOCK EXAMINATION
CODE: 041 BASIC MATHEMATICS
(For Both School and Private Candidates)
TIME: 3 HOURS MAY, 2023
Instructions
- This paper consists of section A and B with fourteen (14) questions.
- Answer all questions.
- Each question in section A caries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- Mathematical tables and non – programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room
- Write your Examination number on every page of your answer booklet(s).
SECTION A (60 MARKS)
1. (a) Simplify the sum of 85% of 9861 and ![]() of 12458. Write your answer correct to two significant figures.
of 12458. Write your answer correct to two significant figures.
(b) (i) Mr. Tumai Distributed Tshs 960,000/= awards to students who passed well in their examinations and their respective teachers as follow: 23% to all students who passed Arts Subjects. 15% to students who passed Mathematics and 27% to students who passed science subjects. The remained amount was distributed to teachers. Find the amount that were awarded to teachers.
(ii) Three bells commence tolling together and toll at intervals of 8, 10 and 12 seconds respectively. How many times do they toll together in 50 minutes?
2. (a) If ![]() . Simplify
. Simplify ![]()
(b) Describe the applications of Logarithm in real life situations
3. In a certain class MSUVA displayed counting numbers less than 30. From the displayed numbers, OKWI mentioned all numbers divisible by 2 and FEITOTO mentioned all numbers that were the multiples of 3.
- (i) Outline all numbers that were mentioned by OKWI and FEITOTO in common.
(ii) How many numbers were mentioned by either OKWI or FEITOTO?
- If a number was selected at random from the numbers displayed by MSUVA, what is the probability that a selected number was a multiple of 3?
4. (a) Given that ![]() = 4i + 3j and
= 4i + 3j and ![]() = 6i – 3j, find the value of “h” and “k” if h
= 6i – 3j, find the value of “h” and “k” if h![]() + k
+ k![]() = 10i + j
= 10i + j
(b) A perpendicular line from the point P(2,-4) to the line meets the line at point Z(-1,3). Find:
i. Distance ![]()
ii. If the point Z(-1,3) is a mid-point of the line ![]() , find the coordinates of point
, find the coordinates of point ![]()
5. (a) In the following figure; ![]() //
//![]() and
and ![]() ; If
; If ![]() and
and ![]() , find the Area of BCDE
, find the Area of BCDE
(b) By considering the Alternating opposite angles theorem, draw the diagram hence identify the corresponding angles.
6. (a) The time “t” taken to buy fuel at LAKE OIL PETROL STATION in Morogoro varies directly as the number of vehicle “V” in the queue and inversely as the number of pumps “P” available in the station. In petrol station with 10 pumps it takes 20 minutes to fuel 40 vehicles.
- Write vehicle “V” in terms of pumps “P” and time “t”
- Find the time it will take to fuel 60 vehicles in a station with 4 pumps.
(b) Mayele bought 3 bottles of juice of capacity 350 ml and Dialo bought 1 bottle of juice of capacity 1 litre.
i. Who had more juice to drink?
ii. How much more?
7. (a) What do the following terms mean as used in Accounts?
- Cash book
- Assets
- Credit transactions
(b) A company bought two cars for Tshs 25,000,000/= each. If one car was sold at a profit of 18% and another was sold at a loss of 6%. In the whole transactions there were no loss. What was the profit made by a company?
8. (a) A BODA BODA driver rates after each kilometre. The fare is Tshs. 1000/= for the first kilometre and raise by Tshs. 500/= for each additional kilometre. If BALEKE want to travel 10 kilometres by BODA BODA. What will he be charged by BODA BODA driver?
(b) The number 19683 is in which term in the following Geometric sequence; 3, 9, 27 …?
9. (a) If the square of the hypotenuse of an isosceles right-angled triangle is 128 cm2 find
the length of each other sides
(b) From the top of a tower of height 60m the angles of depression of the top and the bottom of a building are observed to be 300 and 600 respectively. Find the height of the building.
10. (a) If the length of each side of a square is increased by 6, the area become increased to 16 times the area of the small square. Find the length of one side of the original square.
(b) A large rectangular garden in a park is 120m wide and 150m long. A contractor is called in to add a brick walkway to surround this garden by the same width. If the area of the walkway is 2800m2, how wide is the walkway?
SECTION B (40 MARKS)
11. (a) In certain research the data were summarized as shown in a table below:
| Class Mark | 10 | 15 | 20 | 25 | 30 | 35 |
| Frequency | 3 | 2 | 10 | 5 | 4 | 1 |
By using the data above reconstruct a frequency distribution table including class interval and frequency.
(b) Prove that equal chords of a circle subtend equal angles at a centre.
12. (a) Two towns P and Q on the Latitude 480 are 370 Nautical miles apart. Find the
difference in their longitude.
(b) A pyramid with vertex V and edges VA, VB, VC, VD each 15cm long has a rectangular base ABCD where AB = CD = 10cm and AD = BC = 8cm.
i. Sketch the pyramid using the above information.
ii. Calculate the height “VO” of the pyramid where “O” is the centre of the rectangle.
- Calculate the angle between the base and edge
13. (a). (i). Find the possible values of x if the matrix ![]() has no inverse.
has no inverse.
(ii). By using matrix method, solve the equations
![]()
(b). A transformation is given ![]()
![]() and
and ![]() , find the image of the equation 2x – 3y = 6 under the transformation matrix which performs the above transformations.
, find the image of the equation 2x – 3y = 6 under the transformation matrix which performs the above transformations.
14. (a) A function f is defined as;
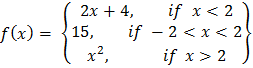
Find (i) f(1.95) (ii) f(15) (iii) Domain of f (iv) identify the type of a function f
(b) A school is preparing a trip for 400 students. The company who is proving the transportation has 10 buses of 50 seats each and 8 buses of 40 seats, but only 9 drivers available. The rental cost for a large bus is 800,000/= and 600,000/= for the small bus. How many buses of each type should be used for the trip for the least possible cost?
FORM FOUR MATHEMATICS EXAM SERIES 127
FORM FOUR MATHEMATICS EXAM SERIES 127
THE UNITED REPUBLIC OF TANZANIA PRESIDENT'S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
ZONAL FORM FOUR MOCK EXAMINATION
(KATAVI, MBEYA, NJOMBE, RUKWA AND SONGWE REGIONS)
041 BASIC MATHEMATICS
Time 3:00 Hours Year: 2022
INSTRUCTIONS
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions
- Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- Mathematical tables and non-programmable calculators may be used.
- All communication devices and any unauthorized materials are not allowed in the examination room
- Write your Examination Number on every page of your answer booklet(s)
- Where necessary, use the following constants
- Pie,
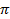 =3.142
=3.142 - Radius of the earth, Re =6400km.
SECTION A: (60 MARKS)
Answer all questions from this section
1. (a)The traffic lights at three different road crossing changes after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m at what time they change simultaneously again?
(b)If x = 0.567567567… and y – 0.8![]() by converting these decimals to fractions, find the exact value of
by converting these decimals to fractions, find the exact value of ![]()
2. (a) If ![]() find the value of t
find the value of t
(b)Write “L” in terms of M, N and T from the formula ![]()
(c) Determine the value of x if ![]()
3. (a)Let ![]() be a universal set and A and B be the subsets of
be a universal set and A and B be the subsets of ![]()
A= {c, g, f} and B= {b, d, h} find
(b)Find the probability that a king appears in drawing single card from an ordinary deck of 52 cards.
4. (a)The coordinate of P, Q and R are (2, m),(-3, 1) and (6, n) respectively. If the length PQ is ![]() units, and the mid-point of QR is
units, and the mid-point of QR is ![]() . Find the possible values of m and n.
. Find the possible values of m and n.
(b)Given vector ![]()
- The victor
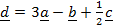
- A unit vector in the direction of vector d
5. (a) Given ![]() where
where ![]() are the sides of the triangle ABT and
are the sides of the triangle ABT and ![]() Are sides of the triangle KLC. What does this information imply?
Are sides of the triangle KLC. What does this information imply?
(b)A regular hexagon is inscribed in a circle. If the perimeter of the hexagon is 42 cm, find the radius of the circle and its area.
6. (a)Twelve people can dig a trench in 15 days for 8 hours daily. How long can they take to finish the same work, working for 10 hours daily?
(b)A variable V varies jointly as the variable A and h. when A=63 and h=4, v=84.
Find;
- V when A=9 and h=7
- A when V=4.5 and h=0.5
7. (a)If a:b=2:3 and b:c=5:6. Find a:c and a:b:c
(b)From the following information given by Mbeya Co.ltd for the year ended 31st December 2021.
Stock (01.01.2021) ………………………….Three quarter of the closing stock
Stock (31.12.2021) ………………………… ![]() of net purchase
of net purchase
Net purchases during 2021 …………………. 432,000.
Gross margin …………………………. 15%
Expenses ……………………………… 20% of Net profit
Calculate;
- Cost of goods sold
- Gross profit
- Net profit
8. (a)If the 5th term of an arithmetic progression is 23 and the 12th term is 37, find the first tem and the common difference.
(b) In how many years would one double one’s investment if Tshs 2500 is invested at 8% compounded semi –annually.
9. (a) If tan A= ![]() , where A is an obtuse angle. Find.
, where A is an obtuse angle. Find.
- Cos A + sin A
- –cos2 A – sin2 A
(b) A and B are two points on the ground level and both lie West of flagstaff. The angles of elevation of the top of the flagstaff from A is 56° and from B is 43°. If B is 28m from the foot of the flagstaff. How far apart are the point A and B?
10. (a)Solve for the quadratic equation x2 – 8x + 7=0
(b)Solve for x and y if ![]()
SECTION B (40 MARKS)
Answer all questions from this section
11. (a)The marks in basic Mathematics terminal Examination obtained by 40 students in one of the secondary school in Katavi were as follows;
60, 54, 48, 43, 37 61, 43, 66, 65, 52, 37, 81, 70, 48, 63, 74, 67, 52, 48, 37, 48 42, 43, 52, 52, 22, 27, 37,44 38, 29, 19, 28 36, 42, 47, 36, 52, 50, 28.
- Prepare a frequency distribution table with class intervals 10 – 19, 20 – 29, etc.
- Find the class which contain the median
- Find the mean
- Calculate the median.
(b) Find the value of angle x in the figure below, where O is the centre of the circle
12. (a)A Rectangular box with top WXYZ and base ABCD has AB=9 cm, BC=12cm and WA=3cm
Calculate
- The length AC
- The angle between WC and AC
(b)Two places P and Q both on the parallel of latitude 26°N differ in longitudes by 40°, find the distance between them along their parallel of latitude.
13. (a)If matrix A is singular, what will be the value of y given that
![]()
(b)Solve the following simultaneous equation by matrix method:
![]()
(c)Find the image of (3, 5) after rotation of 270° about the origin in the anti-clockwise direction.
14. (a)(i)Without using table of values draw the graph of f(x)= x2 + 2x – 4
(ii) State domain and range of f(x)
(b)A transport company is hired to transport 420 people. It has two types P and Q of vehicles to be used. Type P carries 35 passengers and type Q carries 14 passengers. There are at least 10 vehicles of type Q and not more than 9 vehicles of type P. Write inequalities to represent this information
FORM FOUR MATHEMATICS EXAM SERIES 88
FORM FOUR MATHEMATICS EXAM SERIES 88
PRESIDENT'S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
ARUSHA REGIONAL FORM FOUR MOCK EXAMINATION
041 BASIC MATHEMATICS
TIME : 3 Hours July 2022
INSTRUCTIONS
- This paper consists of Section A and B.
- Answer all questions in both sections.
- Each question in section A caries six(6) marks while section B caries ten(10) marks.
- ALL necessary work and answers should be shown clearly.
- Write your NAME on each page of your answer sheet provided.
- USE ?=3.14 and radius of the Earth=6400km
SECTION A (60 Marks)
Answer ALL questions in this section
1. (a) Given x=1.6 x 109 and y= 5.7 x 103. Find z in standard form if
- xy = z
- yz = x
(b)(i) Three cars arrived at Msamvu terminal at the interval of 30 minutes, 40minutes and 55 minutes. If all arrived at Msamvu terminal at 2:00pm on Saturday, at what time would they arrive together?
(ii)Express ![]() in the form of
in the form of ![]() where a and b are integers and b are integers and
where a and b are integers and b are integers and ![]()
2. (a)Solve x and y given that (23x+1) (5y+4) = 20
(b)Without using tables, calculate the value of:
- Log106
- Log10 0.9, Given that log102 = 0.3010, Log10 3=0.4771
(c) If ![]() , Find the value a, b and c
, Find the value a, b and c
3. (a)In a class of 20 pupils, 12 pupils study English but not History, 4 pupils study History but not English and one pupils study neither English nor History. How many pupils in class study History? (Use Venn diagram)?
(b)Inside the class, there are 6 wooden chairs and 8 plastic, two chairs are taken at random from the class without replacement. By using tree diagram, find the probability that the first chair taken is wooden and the second chair is plastic.
4. (a)The line passing though the points A(K,4) and B(3,3k) is to be parallel to the line y – 3x – 4=0. Find the value of K.
(b)Given the vectors ![]()
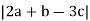
- Scalar t and k if
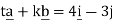
5. (a)Calculate the area of a rectangular plot whose diagonal is 34cm and its perimeter is 92cm.
(b)In the figure below, PQ/BC, PB=3cm, AQ=2cm, BC=6cm, QC=4cm and the area of ![]() APQ=8cm2
APQ=8cm2
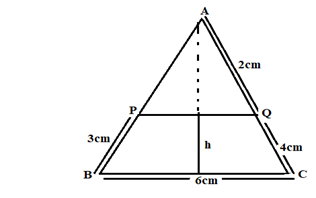
- Show that
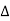 APQ is similar to
APQ is similar to 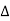 ABC
ABC - Find the area of
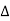 ABC
ABC - Calculate the length of AP and PQ
- Calculate the Height “h”
- (a)If a car travels 120km on 4 litres of diesel, how many litres of diesel are needed to drive 300km?
(b) if y2 varies directly as 1 – x and inversely as x + d and if x =2 and d= 4 for y= 1.
Find x when y = 2 and d=1
(c)If 20 men can dig a trench for laying 6km of water pipe in 10 days, how many Kilometers of water pipe could be laid by 30 men in 15 days?
7. (a)(i) An amount of Tshs 12,000 is to be shared among Sandrah, Neylar and Rachel in the ratio of 2:3:5 respectively. How much will each get?
(ii)Madam Irene bought a book for Tsh 120,000, a year later she sold it at a profit of twenty percent, what was selling price of the book?
(b)Use the following information to prepare the balance sheet of Mr. Oloitipitip as at 31.12.2021
Machine ………………………… 15,000
Drawing ………………………… 10,000
Capital …………………….……. 50,000
Cash …………………………….. 16,000
Furniture ………………………… 25,000
Net Profit …………………… ….. 15,000
Creditors ……………………..…… 5,000
Stock ……………………..……….. 4,000
8. (a)The sum of the first terms of a progression is 5n – 1. Prove that the progression is Geometric Progression.
(b)Nusaybah started a bank account and decided to deposit 15,000/= during the first year, 24,000/= during the second year and an extra 900/= for each additional year. Find the total amount she will have deposited after eleven years.
9. (a) Sin x° = ½. Find
- The value of x
- Tan x° given that x is an angle
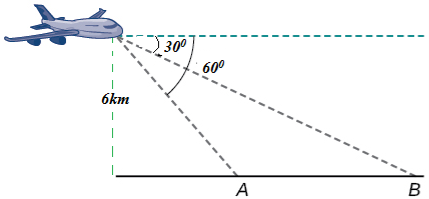
(b)A plane is flying at altitude of 6kn directly over line AB. It spots two boats A and B on the sea. If the angle of depression of A and B from the planes are 60° and 30° respectively, calculate the horizontal distance between A and B
10. (a) If fx2 – 16x + 16 is a perfect square. Find the value of “f”
(b)A garden measured 12m by 16m is to have a pedestrian pathway of equal width constructed all around it, increasing a total area of 258m2. What will be the width of pathway?
SECTION B 40 MARKS
Answer ALL questions in this section.
11. (a) The following are the marks obtained by 30 students in the mathematics
| 34 | 43 | 24 | 30 | 34 | 27 | 33 | 24 | 23 | 23 | 40 | 33 | 25 | 33 |
| 23 | 47 | 23 | 36 | 43 | 16 | 30 | 41 | 23 | 15 | 24 | 20 | 39 | 21 |
| 42 | 23 |
|
|
|
|
|
|
|
|
|
|
|
|
- Draw a frequency distribution table by grouping the marks with the class mark
17, 22, 27 …..
- Calculate mean by using assumed mean method given A=32.
- Draw histogram and use it to estimate mode.
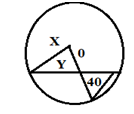
(b)Find the value of x and y if 0 is the center of the circle
12. (a)A ship starts at (60°S, 30°W) and sail due west for 1200 nautical miles finds its new latitude and longitude.
(b)The figure below shows a square pyramid. ABCD is the base in which AB=BC=50cm, each slanting edge such as EC is 70cm.
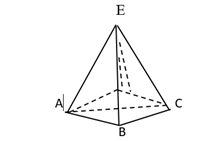
Find
- The angle that a lateral face makes with the base ABCD.
- The total surface area of the pyramid
- The volume of the pyramid
- (a)Given matrix
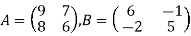
Find;
- AB
- BA
- Comment on the results obtained in (i) and (ii) above.
(b) Let ![]() find
find
- T-1
- Use the answer obtained in (b) above to solve the equation
![]()
(c)Find the image of the point (1, 2) after a reflection in the line y + x=0.
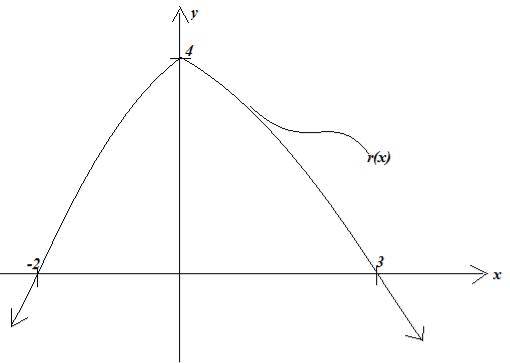
14. (a) Given the figure below, Determine r(x)
(b)Holiness wants to buy oranges and mangoes for her children. The oranges are sold at Sh.150 each and mangoes at sh 200 each. She must buy at least two of the kind of fruits but her shopping bag cannot hold more than 10 fruits. If the owner of the shop makes a profit of shs. 40 on each orange and sh 60 on each mango, determine how many fruit of each kind Holiness should buy for the shop to realize the maximum profit.
FORM FOUR MATHEMATICS EXAM SERIES 65
FORM FOUR MATHEMATICS EXAM SERIES 65
PRESIDENT'S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
KILIMANJARO REGIONAL COMMISSIONER'S OFFICE
FORM FOUR MOCK EXAMINATIONS
BASIC MATHEMATICS
CODE: 041
TIME:3HOURS 27/06/2022
INSTRUCTIONS
l . This paper consists of sections A and B
2. Answer all questions in section A and B
3. All necessary working and answer for each questions must be shown clearly
4. NECTA mathematical table and non-programmable calculator may be used
5. Cellular phones and any unauthorized materials are not allowed in the examination room.
6. Use π=3.14
SECTION A (60 Marks)
Answer all questions in this section
1. a) Mangoes are to be exactly divided into groups of 20, 30 or 36. What is the smallest number of mangoes required?
b) Anna was given 60,000 shillings by her mother she spent 35 percent of the money to buy shoes and 10 percent of the remaining money to buy books. How much money remained?
2. a) If log y + 21og (3x+ l) = l . Express y in terms of x
b) Given a recurring decimal 0.9666666... write it as a fraction.
3. a) Simplify
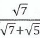
by rationalizing the denominator
b) A box contains 4 defective transistors and 12 good transistors. If two transistors are drawn from the box without replacement. What is the probability that
(i) The first is good and the second is defective
(ii) One of the transistor drawn is good and the other is defective.
4, a) There are 48 men at a meeting of whom 24 are teachers, 36 are parents and 16 are both teachers and parents. By using Venn diagram, find the number of men who are neither a teacher nor a parent.
b) Find the direction cosine of c= 9i + 12j, hence show that the sum of the squares of these directions cosine is one.
5. a) Find the equation of the line through the points (4, 6) and the midpoint of (2, 4) and (1 0, 4)
b) The length of two sides of a triangle are 16cm and 20cm . Find the area of the triangle if the included angle is 360
6. a) In the preparation of Fanta orange drink a bottle machine can fill 1500 bottle in 45 minutes. How many bottle will it fill in 4 1 /2 hours ?
b) The mass (m) which can be supported by a beam varies directly with the breath (b) and inversely with the length (l) . If a beam of breath 2m and length 15m can support a mass of 200kg. What mass can be supported by a beam which is 3m broad and 20m long?
7. a) John wants to invest a certain sum of money so that its value after 3 years will be 100,000/= shillings.How much amount of money should be invested at 5% per annum compound interest?
b) Study the given trial balance and answer questions that follow:
Trial Balance as at December 2021
| SIN | Details | Amounts(Tshs) | Amount(Tshs) |
| l. 2. 3. 4. 5. 6. 7. 8. | Cash Capital Purchases Sales Water bills Advertising Telephone bills Salaries | 185,000.00 110,000.00 3,000.00 2,000.00 I ,000.00 3,000.00 | 200,000.00 104,000.00 |
| | | 304,000.00 | 304,000.00 |
Prepare the balance sheet
8. a) The first term of an arithmetic progression is 12 and the common difference is 10 . Find nth term.
b) A farmer wants to plant 6 mangoes seedling in a row at a fixed interval of 7 metres. Determine the length of the row.
9. a) A ladder leans against a vertical wall . If the ladder reaches 12m up the wall and its foot is 9m from the base of the wall, find the length of the ladder.
b) Given that A and B are complementary angles and sin A= 3/5 Find tan B (Leave your answer as improper fraction)
10 .a) Solve the following equation by completing the square method 2x2+ I Ox - 28 = 0
b) The difference between two positive numbers is 7 if their product is 30. Find the numbers.
SECTION B (40 Marks)
Answer all questions in this section
I l . The number of patients who attended maternity clinic daily in June 2020 in a certain town was recorded
51 61 70 75 70 74 73 72 82 70 71 76 74 68 65 72 69 64 83 63 83 58 80 90 50 89 55 62 61 62
a) Prepare a frequency distribution table with class size 5 beginning with the number 50 taking into consideration that both lower limit and upper class limit are inclusive
b) Calculate the mean and mode from the frequency distribution table prepared in
(i) above by using assumed mean from the class mark of the modal class.
c) Draw a cumulative frequency curve and use it to estimate the median.
12 a) The following figure represents a rectangular pfism in which PQ=12cm, QR=8cm and RY=4cm
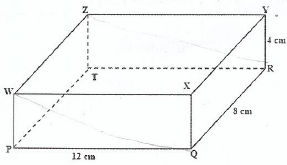
Find;
(i)The total surface area.
(ii)The angle between the planes PTZW and QRZW
(b) A and B are two points on latitude 70N. Their longitudes are 620 W and 1180 E respectively. Calculate the distance in kilometres from A to B if the earth's diameter is 12800km for the following cases
i. Along the great circle route over North Pole
ii. Along the parallel of latitude![]()
13. a) i. Given the matrix
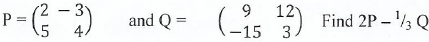
ii. If the matrix

is singular, find the possible value of k
b) By using the transformation matrix (10 -01) Find the image of the point A( -2 , 3)
Hence state the axis in which this point is reflected .
c) Solve the following system of linear equation by using the inverse matrix method
2x + 3y=7
y=½x
14. (a) Given
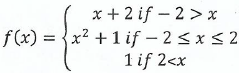
![]() Sketch the graph of f(x)
Sketch the graph of f(x)
ii. from the graph state domain and range
b) A business plans to buy at most 210 sacks of Irish and sweet potatoes .1rish potatoes costs shs 30,000 per sack and sweet potatoes costs shs 5000 per sack. He can spend up to shs 2,500,000 for his Business. The profit on a single sack of Irish potatoes is shs 12,000 and for sweet potatoes is shs 10,000. How many sacks of each type of potatoes the business man will buy in order to realize the maximum profit?
FORM FOUR MATHEMATICS EXAM SERIES 47
FORM FOUR MATHEMATICS EXAM SERIES 47
PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
KIBAHA PRIVATE SECONDARY SCHOOLS ASSOCIATION (KIPSSA)
FORM FOUR PRE – MOCK EXAMINATION – 2022
BASIC MATHEMATICS
CODE: 041
TIME: 3:00 Hours JUNE 2022
Instructions
1.This paper consists of sections A and B with a total of fourteen (14) questions
2.Answer all questions in section A and B.
3.Each question in section A carries six (6) marks while each question in section B carries (10) Marks.
4.All necessary working and answers for each question must be shown clearly.
5.NECTA Mathematical tables and non-programmable calculators may be used.
6.All communication devices and any unauthorized materials are no allowed in the examination room.
7.Write your Examination Number on every page of your answer booklet(s).
SECTION A
1. a) Use the number line to find the value of -3×-4
b) A village received 452009 bags of fertilizer to be distributed to 4500 Farmers. Estimate the number of bags each farmer got?
2. (a) Given 5××(25)2y = 1 and 35×× 9y = 1/9. Find the value of x and y.
(b). Given that Log x =4?.0524, find log ?x
3. (a) E S GO Company a hosted a birthday part of 300 people out of 300 Participants, a group of 200 participants took at least one of the drinks, Coca-Cola, Pepsi and Fanta. A report given by serves revealed the drinks the following numbers of participants to have taken the indicated drinks. Coca cola 132, Pepsi 78, Fanta 120, Pepsi and cola-cola 36, Coca-Cola and Fanta 90,pespsi and Fanta 24.How many participants took
i. All the drinks
ii. Coca-Cola but not Fanta
b). A bag contains 3 red discs, 4 blue discs and 5 green discs. A trial consisting of selecting a disc at random noticing its colour and then replacing it .If two trials are done, what is the probability of the selecting
i. Two red discs
ii. One green disc and one blue disc
iii. Two blue discs
4. a) Given that; a = 6i-2j, b = 2i +j and c= 3i-5j.
Find; (i) 2a + b- 3c
(ii) t and k; ta +kb = 4i – 3j
b) Find the equation of a line parallel to y-axis, and cuts the x-axis at 2.
5. (a) The diameter of a circular park is 28 meters.
A road of 1.75 meters wide run around it .find the cost of gravelling the road at 65/= per square meter.
b) Draw a right angled triangle ABC <90 is at B, such that AB=5cm and BC = 12 cm. Measure 3cm from B toward A, and draw a straight line from that new point (mark it D) toward the line AC, and mark a new point E , BC// DE. What is DE?
6. (a)Alex began his journey at 8:55 am After one hour and forty minutes he meet his friend Juma the two talked for the thirty five minutes, then Alex continued his journey. Two hours and forty six minutes later he arrived where was going. How long did the journey take?
b) Two taps A and B can fill a tank in 3 and 4 minutes respectively. They both run until the tank is half full and then tap A is shut off while tap B remains running. Find the total time to fill the tank.
7. (a) The profit of an item costing Tsh: 6000/= is decreased by 380/= when its sells price is reduced by 5%
Find (i) the sales price
(ii) the percentage profit before reduction
b) the information below refer to Mr CAVAN business Enterprises Ltd. On
- January 1,2020;he commenced business with a capital 2,000,000/=
- 2nd January 2020, bought goods for cash 500,000/=
- 4th January 2020, paid rents for 50,000/=
- 5th January 2020, received cash from john 200,000/=
- 6th January 2020, sold goods for cash 700,000/=
- 8th January 2020, paid electricity bill for cash 30,000/=
- 10th January 2020, cash sales 250,000/=
- 13th January 2020,purches goods for cash 350,000/=
- 17th January 2020, drew cash 150,000/=
- 26th January 2020, cash purchases 320,000/=
Prepare a cash book A/C
8. (a) A lecture hall has 20 rows of a seats with 100 seats in the back row, each row have 2 fewer number of seats than the row immediately behind it .How many seats are their in the lecture hall?
(b) Mabrouk invested a certain amount of money in a saving account whose interest rate was 8% compounded annually .After three year ,he got 500,000/=
(i) How much did the invest at the start.
(ii) How much did he received as interest at the end of 3 years?
9. (a) From the top of the building 60m high the angle of depression of the top and the foots of lamp post are 300 and 600 respectively .what is height of the lamp post?
(b) calculate the altitude of an equilateral triangle with sides each 8cm long .
10. (a) Find quadratic equation whose solution set is {-3,5}
(b) Twice one number added to three times another gives 21 .Find the if the difference between them is 3.
SECTION B.
11. (a) In a competition, 30 children had to pick up as many paper clips as possible in one minutes. Using pair of tweezers and the results were as follows
3, 17, 8, 11, 26, 23, 18, 28, 33, 38, 12, 38, 22, 50, 5, 35, 39, 30, 31, 43, 27, 34, 25, 39, 14, 2 7, 16, 33, 49.
(i) Construct a frequency table use in 1-10, 11-20 and etc. and hence sketch the commutative frequency curve.
(ii) From the curve estimate median number of clips picked up
(iii) Calculate the mean use in the original data
(b) AO is parallel to BC and OBC =58 .Find AOB,A?B and C?B
12. (a) Two point P and Q are on parallel latitude 260 N differ in longitude by 400 how long will it take an aero plane to travel from point P to Q with speed of
27.534. knot? use earth radius R =6400km and ? = 3.14)
(b) VABCD is a pyramid with the rectangular base ABCD in which AB = 12cm and BC = 5cm .V is a vertically above the center of the rectangle and VA = VB = VC = VD =10cm.sketch the pyramid hence find (i) The angle between VA and the plane ABCD.
(ii) The angle between lateral face and the base.
13. (a)If

and
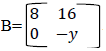
Find x and y, Given that A2 = B + I, WHRE I is identify matrix.
(b) Find the equation of the line 3y =4x-2 after a reflection in the line x-y = 0.
14. (a) A tailor has 96 meters of cotton materials and 72 meters of woolen materials. It takes 1.5 meters of cotton and 1 meter of woolen to cotton a suit, while a dress requires I meter of cotton and 2metre of woolen. If a suit for Tsh: 30,000/= and dress for Tsh:25,000 By defining cleary the decision variables , formulate all constraints and objective function to be used to optimize sells.
(b) Given f(x) = X2+X-6 for -5?X ?5.Draw the given graph of f(x) and use it to find the solution set of the equation x2 + x - 12 = 0
FORM FOUR MATHEMATICS EXAM SERIES 44
FORM FOUR MATHEMATICS EXAM SERIES 44
THE UNITED REPUBLIC OF TANZANIA ,PRESIDENT'S OFFICE, REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
MBINGA TOWN COUNCIL
FORM FOUR MOCK EXAMINATION -2022
CODE: 041 BASIC MATHEMATICS
TIME: 3:00 HRS June, 2022
1. This paper consists of section A and B with a total of fourteen (14) questions.
2. Answer ALL questions in section A and B.
3. Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
4. ALL necessary working MUST be shown clearly for each question attempted
5. Mathematical Tables, non-programmable calculators and graph papers may be used.
SECTION A (60 MARKS)
Answer all questions in this section
1. (a) A red light flashes on every 8 seconds and a green light flashes an every 10 seconds. If the two lights are switched on at the same time, after how long will both lights flash on together?
(b) There were 66 people on a bus. At the first stop, 28 people got off. And 19 people got on. At the next stop, five people got off and 13 people got on how many people were there on the bus now?
2. (a) Given that x= 3![]() and y = 2√3 , Simplify the following expression
and y = 2√3 , Simplify the following expression
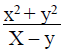 in the form of a
in the form of a![]()
(b) Solve the value of ‘x’ if, log (2x + 1) – log (3x-2) =1
3. (a) Five girls and three boys put their names in a box, one name is picked out at a random without replacing the first name, a second name is picked out at random. What is the probability that both are names of girls? (b) A and B are subsets of universal set U. find
n (A n B) given that n(A) = 39, n (A' n B') = 4, n(B') = 24 and n(U) = 65
4. (a) A line passing through point A (t, 4) and B (3,2t) is parallel to the line. y + 3x – 4 = 0 find the value of t
(b) A boat crosses a river at a velocity of 20km/h southwards. The river has a current of 5km/h due east. Calculate the resultant velocity of the boat.
5. (a) Two regular flags are similar in shape. Their areas are 5m2 and 0.8m2. If the height of the smaller flag is 180cm, calculate the height of the larger flag.
(b) In ![]() ABC, M is on AB with AM = 4cm and MB = 2cm. N is on AC, and MN is parallel to BC
ABC, M is on AB with AM = 4cm and MB = 2cm. N is on AC, and MN is parallel to BC
i. Show that ![]() AMN is similar to
AMN is similar to ![]() ABC
ABC
ii. If BC = 4.5 cm Find MN
6. (a) A pickup truck was carrying maize having a mass of 1 tone 40kilograms and potatoes of mass 280 kilograms. A further 500 grams of spinach were put on top. Find the total mass of the foods being carried.
(b) A quantity of lead is made into small spheres. The number N of spheres varies inversely as the cube of the radius r mm. if r = 0.5 then N = 4,000
i. Find N in terms of r
ii. How many spheres of radius 0.8mm can be made?
7. (a) Joyce, Amina and Shabani are 10 years old, 12 years old and 8 years old respectively. They are given 45,000/= to share in the ratio of their ages. How much does each one get?
(b) Mr. Kapinga found in his business the following transaction informations, at the end of business year December 2005 .
Opening stock on 1st January 2005 ………………. 34,430
Net purchases during 2005 ………..…. 219, 290
Closing stock on 31st December, 2005 ……...…… 26,720
Sales ………………… 340, 500
Expanses for the year ……………………. 45,880
Use the above information to find
(i) Cost of goods sold
(ii) Gross profit
(iii) Net profit
8. (a) One day Anna spends 40 minutes on her home work. The length of time she spends increases by 4 minutes each day. Find the total length of time she has spent after eight days?
(b) The third term of geometric sequence is 3 and the sixth term is 24. Find the first two terms.
9. ![]() (a) Ndunguru stands 200m from a base of a tall building. The angle of elevation of the top of the building is 24. What is the height of the building?
(a) Ndunguru stands 200m from a base of a tall building. The angle of elevation of the top of the building is 24. What is the height of the building?
(b) Simplify the following
i. sin 33° cos 57° + cos 33° sin 57° ii. Cos (30° – 45°)
10. (a) Amina is 6 years younger than her brother Yusuph. If the product of their ages is 135. Find how old is Amina and Yusuph?
(b) If x2 + y2 = 4 and (x + y)2 = 10 find xy
SECTION B (40 MARKS)
Answer all questions in this section.
11. (a) The masses in kg to the nearest kg of 40 people are as follows.
| 59 | 54 | 51 | 59 | 61 | 60 | 61 | 59 | 58 | 56 |
| 62 | 61 | 63 | 58 | 57 | 56 | 60 | 62 | 60 | 64 |
| 61 | 65 | 58 | 54 | 52 | 62 | 67 | 69 | 49 | 57 |
| 56 | 58 | 60 | 62 | 58 | 51 | 57 | 70 | 63 | 60 |
(i) Make a frequency distribution table using each class size of 5, and the lower limit of the first class interval to be 46
(ii) Use the frequency distribution table obtained to find the actual mean.
(b) Prove that the sum of opposite interior angles of cyclic quadrilateral are supplementary.
12.(a) The figure below is a pyramid of rectangular base PQRS of length 12cm and width 9cm, the slanting edge has a length of 19.5cm
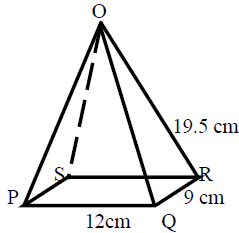
(i) Determine the height of the pyramid
(ii) The angle formed by a line PO and base PQRS
(b) Calculate the distance between P (50° N, 12°W) and Q (50°N, 26°E). Give your answer in nautical miles (nm)
13.(a) Find the image of B (3,4) after a reflection in the line y = -x followed by another reflection in the line y = o (b) Determine the value of x for which the matrix ![]() has no inverse.
has no inverse.
(c) Given A = ![]()
find:-
(i) A-1
(ii) Use your answer in (i) To solve the equation
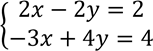
14.(a) A linear function is such that f(1) = 2 and f(3) =8 .
Find f(−1) if f(x) =
FORM FOUR MATHEMATICS EXAM SERIES 43
FORM FOUR MATHEMATICS EXAM SERIES 43
THE UNITED REPUBLIC OF TANZANIA PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
LUDEWA DISTRICT CONCIL
FORM FOUR MOCK EXAMINATION 2022
041 BASIC MATHEMATCS
(For Both School and Private Candidates)
TIME: 3 Hours 07th JUNE 2022
Instructions
1. This paper consists of section A and B with a total of fourteen (14) questions
2. Answer all questions
3. Each question in section A caries six (6) marks while each question in section B carries ten (10) marks
4. All necessary working and answer for each question must be shown clearly
5. NECTA mathematical tables and non- programmable calculators may be used
6. All communication devices and any unauthorized material are not allowed in the examination room
7. Write your examination Number on every page of your answer booklet(s)
SECTION A (60 MARKS)
Answer all questions
1. (a) Three boys rang the ball at different regular intervals. The first boy was ringing after every 10 minutes, the second after 25 minutes and the third at every 40 minutes. If at the start, they all rang the bell at 6:45 a.m, when the bell rang again by all the three boys?
(b) Alex is making some small metal rods. He has three pieces of metal of length 432 cm, 648 cm and 540 cm. what is the longest length of rod can make if the rods have the same length and no metal is wasted?
2. (a)Jacob is looking for the error when running the program in his computer, in order the program to run. The message error when coding shows that, the program may run if the value of a is known in log4(a + 5) = 2. What is that?
(b) What do you think it is the value of ![]() ?
?
3. (a) A study of food preference on three types of food: Potatoes, Rice and Ugali, done on a group of students, revealed the following: 45% likes potatoes, 50% likes Rice, 54% likes Ugali, 22% likes both potatoes and Rice, 20% likes both Rice and Ugali, and 24% likes Potatoes and Ugali. 5% do not like any of these types of foods.
(i) What percentage of students like Rice and Potatoes but not Ugali?
(ii) How many does not like Ugali if the number of those likes Potatoes and Rice only is 20 students?
(b) A box contains two red balls, x blue balls and 4 yellow balls. If the probability of drawing a blue ball from the box is 1/3, how many blue ball must be added in the box to make the probability of drawing a yellow ball to be 1/3.
4. (a) The lines 2x + 3y − 17 = 0 and 3x − 4y = 0 meet at A. Find the equation of a line through A which is perpendicular to the line 2x + 3y = 17 in the form ax + by = c
(b) An aircraft sets a course of 100o and flies at 300km/h. The wind blows at 120km/h from the South-West. Use components to find the actual velocity with which the aircraft will travel.
5. (a) The square is inscribed in a circle of radius r. Find the area and its perimeter in terms of r.
(b) The areas of two circles are in the ratio 48:27. Calculate the radius of the smaller circle if the radius of the large one is 24 cm.
6. (a) Salome, Jeny, Anna and Theresia can eat 2 bags of rice in 12 day. Each bag weighs 10 kg. How many people can eat 6 bags of the same weight in 18 days?
(b) The variable y is directly proportional to the square root of x and x is multiplied by n. what is the ratio of the first y to the secondy?
7. (a)The market price of an article is Tsh 15,000. How much does the article cost after a discount of 5.2% is given?
(b) From the following data, prepare a trading account to find out Gross profit or Gross loss.
- Sales for the year was 36000
- Purchases for the year was 2000
- Stock was at start 500
- Stock was at close 750 for the year 2021
8. (a) If the sum of the first three terms of geometric progression is 18 more than the sum of the first two terms. Compute for the sum of the first four terms of this progression.
(b) Find the amount of money and compound interest accumulated at the end of 3 years after investing Tsh 500,000, at a compound interest rate of 10% annually.
9. (a) P and Q are two pegs on level ground, and both lie due west of a flagstaff are 45o and 60o respectively. Given that P is 24 m from the foot of the flagstaff. Determine the distance PQ.
(b) A rectangular paddock of 80 m long is to be fenced with a wire. If a diagonal of the paddock is 100 m long, what length of fencing wire needed to completely surround the paddock?
10. (a) The area of a rectangle is 21 cm2 which is equal to (2x2 + 5x + 3)cm2. Find the perimeter of this rectangle.
(b) The product of two odd numbers is 255. Determine their sum.
SECTION B (40 MARKS)
Answer all questions
11. A Tailor’s association surveyed the number of sewing machines that each primary association had and recorded as follows:
5, 3, 8, 5, 4, 5, 5, 6, 7, 7, 4, 6, 6, 7, 4, 4, 6, 7, 5, 3, 4, 7, 5, 7, 8, 3.
From this data:
(a) Determine the modal value(s) of the data.
(b) Find the mean value of the data.
(c) Find the median value of the data.
12. (a)Find in nautical miles the distance between two places which lie on the Equator and have longitude of 56o W and 39o W.
(b) A rectangular prism with plane-bases ABCD and EFGH is such that AB=EF=20cm, BC=FG=16cm, and CG=6cm.
(i) Find the angle made between the line AG and the ABCD. (ii) Work out for the volume of the prism.
13. (a) Mariam buys 20 oranges, 4 mangoes and 2 bananas; James buys 20 oranges, 3 mangoes and 4 bananas; Neema buys 8 mangoes. Represent this information in a matrix form.
(b) The matrix ![]() has no inverse. Find the value of x .
has no inverse. Find the value of x .
(c) Determine the new position of the point (-2,2) after a reflection in the x = −3 followed by a rotation through 90o about the origin anticlockwise.
14. (a)The function f is defined as
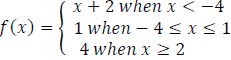
State domain and range of f.
(b) Mwakaleli wants to distribute parcels, using either a lorry or a van. A lorry can carry 200 parcels and costs Tsh 15,000 to hire, and a van can carry 80 parcels and costs Tsh 10,000 to hire. There only 20 men available, of whom only 15 are allowed to drive a lorry. The budget for the distribution is Tsh 260,000.
Find the greatest number of parcels that can be distributed.
FORM FOUR MATHEMATICS EXAM SERIES 42
FORM FOUR MATHEMATICS EXAM SERIES 42
OFFICE OF THE PRESIDENT, MINISTRY OF EDUCATION AND VOCATIONAL TRAINING
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
MOCK EXAMINATIONS- JUNE 2022
041 BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 Hours Year: 2022
Instructions
l . This paper consists of sections A and B with a total of sixteen (16) questions.
2. Answer all questions in section A and only 4-questions in section B..
3. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
4. All necessary working and answers for each question must be shown clearly.
5. NECTA mathematical tables and non-programmable calculators may be used.
6. All communication devices and any unauthorised materials are not allowed in the examination room.
7. Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1(a). If![]() and
and ![]()
Find ![]() correct to two significant figures
correct to two significant figures
(b)Given the number A= 2.489 and the number B = 0.00342
- Write the number A correct to two decimal places
- Write the number B correct to significant figures.
2(a). The L.C.M of 3, x, 8 is 24. Find the value of x given that 3 > X < 8. Give two possible values
(b)3 balls A, B and C ring after 4 sec, 6 sec. and 8 sec respectively when the balls start ringing at a given time, at what time will they ring together again?
(c)Solve the following equations and inequality
3(a). Solve the equations
(b)(i)![]()
(ii)![]()
(c)Given that ![]() and
and ![]() use logarithm to solve the equation
use logarithm to solve the equation ![]()
4(a). Solve the following simultaneous equations
(b)If ![]() where A is acute and B is obtuse find
where A is acute and B is obtuse find
5(a). Factorize the expressions
(b)Express ![]()
(c)Expend P(P+1) – q(q + 1) and factorize the expression
6(a)(i). Given the vectors ![]() j, Find
j, Find ![]() and direction if the vector
and direction if the vector
(ii)If ![]() find the scalars
find the scalars ![]() and X
and X
If ![]() What is the relation between the vectors
What is the relation between the vectors ![]()
(b)Find unit vectors in the direction of the vectors
(c)Force F1 and F2 of magnitude 20N and 30N act in the direction of the vectors a and b respectively
Express the forces F1 and F2 in terms of i and j
7. (a) What do the following terms mean as used in Accounts?
(i) Trading account
(ii) Profit and loss account
(iii) Balance sheet
(iv) Cash account
(b) A car which its buying price was shs 12,500,000 was sold at a loss of 20 percent. Find the loss made and selling price.
8(a). Find without using tables the value ![]()
(b)Simplify (i)![]() (ii)
(ii)![]()
(c)If Sin ![]() , Find all values of x where 0 ≤ x ≤ 360°
, Find all values of x where 0 ≤ x ≤ 360°
9(a). In the triangle ABC below the coordinates of A, B and C are respectively (2, 3), (8, 4) and (4, 6)
- Find the equation of the line passing through C perpendicular to AB
- The equation of the line medial to AB
(b)Given that
AX= 16
XC= 14
BC=35
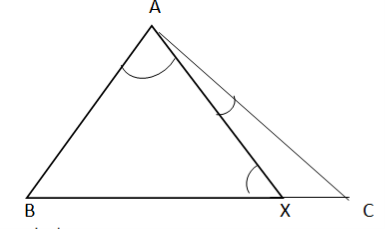
Find
- AB
- AC
 =
=
 =
=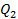
10(a). Given the universal se E
![]()
![]()
Represent the above sets in a Venn-diagram
Write down the elements of (i)![]() (ii)
(ii)![]()
(iii)Verify that
![]() and
and ![]()
(b)In a triangle ABC the ratio of the angles is A: B:C= 2:3:7 The length of the shortest side = 5cm. Find the length of the longest side
(C)(i)How terms are there in the A:P 2 + 5 + 8 + 11 + ……………59
(ii) The sum of the first n-terms of G.P is 3n – 1
Find: The first term and common ratio sum of the first 10 terms
SECTION B
Attempt ANY (4) Questions
11. A density wishes to mix together two kinds of food so that the vitamin content of the mixture contains at least 9-units of vitamin A, 7 units of vitamin B, 10 units of vitamin C and 12 units of vitamin D. The vitamin content per kg. of each food is shown below.
| VITAMIN | A | B | C | D |
| FOOD I | 2 | 1 | 1 | 1 |
| FOOD II | 1 | 1 | 2 | 3 |
If food I costs 500/= per k gm and food II costs 200/= per k gm. Write down
- Add constraints (inequalities) in terms of x and y
- The objective function P (x, y) = 500x + 200y
Where
![]()
Find the number of k gm of food I and food II the dentist should buy so as to minimize costs
12. If ![]() .
.
Find the coordinates of the images of A (1,0), B (1,1) and C (0,1) under this transformation
(b)T is a translation by a vector![]() and M is the reflection in the line y=x
and M is the reflection in the line y=x
Find the image of (2, -1) under the composite transformation MT
(c) T is a linear transformation. If T(h)= (3,4) and T(V)= (-2,2).
Find: (a)T (3V) (b) T (2U-3V)
13(a). Given ![]()
Find the inverse of the matrix A and use the result to find a matrix B such that AB=C
(b)Given the matrix ![]()
And P ![]() such that
such that ![]() , Find the elements of P
, Find the elements of P
(c)Determine the matrix A from the equation.
![]()
14(a). The function f is defined as follows
![]()
- Sketch the graph of f(x)
- Determine the domain of f(x)
- Determine the range of the function
(b)The probability that a certain team T wins a match is 2/3 If the team plays two consecutive games (first and second), Find the probability that;
- It wins all the two games
- It wins only one game
- It loses all the games
- It wins at least one game
(c)
ABCD is a parallelogram
AB= 5
LC = 2
AD = 4
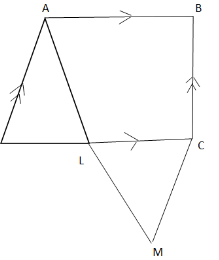
Show that ![]() Find the value of x
Find the value of x
15(a) A right square pyramid TABCD represent an aluminium roof of a Kiosk.
Each slanting height is 5m long
The top wall is 4m log
Calculate:
- The length TM where M is the mid-point of BC
- The angle of elevation of M from T
- The surface area of the root.
(b) The location of four places A, B, C and D on the earth’s surface are A(30°S, 30°W), B(30°N, 30°E), C(30°S 30°W) and D(30°S, 30°E)
Calculate; the distances
(i)AB (ii)CD (iii)AC (iv)BD
Given the radius of the earth R![]()
16.The following distribution table shows the scores of 64 students in a mathematics weekly test.
| CLASS | FREQ f | CLASS MARK | f |
| 30-39 | 5 |
|
|
| 40-49 | 10 |
|
|
| 50-59 | 15 |
|
|
| 60-69 | 17 |
|
|
| 70-79 | 4 |
|
|
| 80-89 | 6 |
|
|
| 90-99 | 7 |
|
|
|
|
|
|
|
- Complete the table and find
 and
and 
- Calculate the mean
- Construct an ogive (o give) and use it to estimate the
- Find the mode class and find the mode
FORM FOUR MATHEMATICS EXAM SERIES 17
FORM FOUR MATHEMATICS EXAM SERIES 17
THE UNITED REPUBLIC OF TANZANIA PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
MWANZA CITY JOINT EXAMINATION (NYEGEZI, BUTIMBA AND MKUYUNI WARDS)
FORM FOUR PRE - MOCK EXAMINATION-2021
041 BASIC MATHEMATICS
Time: 3 Hours MAY, 2021
Instructions
- This paper consists of section A and B with a total of fourteen (14) questions
- Answer all questions in sections A and B, each question in section A carries six (6) marks while each question in section B carries ten (10) marks
- NECTA Mathematical tables may be used
- Cellular phones, calculators and any unauthorized materials are not allowed in the examination room
- Write your examination number on every page of your answer sheet (s)
SECTION A (60 MARKS)
Answer all questions in this section
1. (a) Simplify ![]() without using mathematical table express your answer in four significant figures.
without using mathematical table express your answer in four significant figures.
(b) Jenk and Jemry are riding on a circular path. Jenk completes a round in 24 minutes where as Jemry completes a round in 36 minutes. If they started at the same place and time and go in the same direction, after how many minutes will they meet again at the starting point?
2. (a) Use mathematical table to evaluate ![]()
(b) Find the value of x and y if ![]() = 2025
= 2025
3. (a) Let U be a universal set and A and B be the subsets of U where![]() ,
, ![]() and
and![]() .
.
- Find the number of subsets of set A’
- Find
- If an element is picked at random from the universal set (u), find the probability that it is an element of set B
(b) Find the probability that a king appears in drawing single card from an Ordinary deck of 52 cards
4. (a) The coordinate of P, Q and R are (2, m), (-3, 1) and (6, n) respectively. If the length of PQ is ![]() units and midpoint of QR is
units and midpoint of QR is ![]() find the possible value of m and n
find the possible value of m and n
(b)The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
is -2. Another line L2 is perpendicular to L1 and passes through (-3,-2). What is the equation of L2
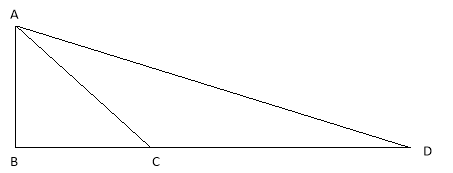
5. (a) if ![]()
![]() and angle ABD =
and angle ABD = ![]() Calculate the length
Calculate the length ![]()
(b) (i) Given ![]() =
= ![]() =
= ![]() = 3 where
= 3 where ![]() ,
,![]() and
and ![]() are the sides of the triangle ABT and
are the sides of the triangle ABT and ![]() ,
,![]() and
and ![]() are the sides of the triangle KLC. What does this Information imply?
are the sides of the triangle KLC. What does this Information imply?
(ii) A regular Hexagon is inscribed in a circle if the perimeter of the hexagon Is 42cm, find the radius of the circle and its Area
6. (a) If y varies inversely as ![]() and x is multiplied by n. What is the ratio of the first y to the second y?
and x is multiplied by n. What is the ratio of the first y to the second y?
(b) The headmaster has enough food to last for his 600 students for 20 days from tomorrow. If 120 students leave the school today for UMISSETA game, how long will the food last?
7. (a) By selling an article at shs 22,500/= a shopkeeper makes loss of 10%. At what price must the shopkeeper sell the article in order to get a profit of 10%?
(b) The following trial balance was extracted from the books of Nzilandodo on 31st December 2005.
TX MARKET LTD TRIAL BALANCE AS AT 31.12.2005
| DETAILS | DR | CR |
| Capital | 15000/= | |
| Drawings | 2410/= | |
| Purchases | 44280/= | |
| Sales | 69470/= | |
| Returns inward | 1200/= | |
| Returns outward | 980/= | |
| Furniture | 2000/= | |
| Motor vehicle | 5000/= | |
| Carriage inward | 14880/= | |
| Rent | 1920/= | |
| Insurance | 370/= | |
| Stock, January | 850/= | |
| Carriage outward | 6290/= | |
| Advertising | 380/= | |
| Cash in bank | 1210/= | |
| Cash in hand | 2780/= | |
| Discount allowed | 120/= | |
| Discount received | 310/= | 550/= |
| Debtors | 6000/= | |
| Creditors | 4000/= | |
| 90000/= | 90000/= |
Note: Stock at close 31st December 7360. Required, prepare balance sheet as that date.
8. (a) The sum of the first six terms of an A.P is 72 and the second term is seven times the fifth term.
- Find the first term and the common difference
- Find the sum of the first ten terms
(b) Find the sum of the first four terms of a geometric progression which has a first term of 1 and a common ratio of ![]()
9. (a) If tan A = ![]() , where A is an obtuse angle,
, where A is an obtuse angle,
Find (i). Cos A + Sin A (ii). – Cos2 A – Sin2 A
(b) A and B are two points on the ground level and both lie west of flagstaff. The angle of elevation of the top of the flagstaff from A is 560 and from B is 430. If B is 28m from the foot of the flagstaff. How far apart are the points A and B?
10. (a) Solve the quadratic equation x2 – 8x +7 = 0
(b) A field is 10m longer than its wide. The area is 7,200m2. What is the width?
SECTION B (40 marks)
Answer all questions in this section
11. ( a) Consider the following frequency distribution tale below;
| Marks | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 | 100-109 | 110-119 |
| Freq | 1 | 2 | 5 | 11 | 21 | 20 | 17 | 10 | 6 | 4 | 2 | 1 |
Draw the histogram and use it to estimate the mode in one decimal place.
b) Find the value of angle X in the figure below.
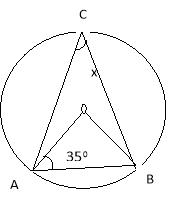
12. (a) A rectangular box with top WXYZ and base ABCD has AB=9cm, BC=12cm and WA = 3cm

Calculate (i) The length AC (ii) The angle between WC and AC
(b) Two places P and Q both on the parallel of latitude ![]() N differ in longitudes
N differ in longitudes
by ![]() find the distance between them along their parallel of latitude.
find the distance between them along their parallel of latitude.
- (a) If matrix A is singular, what will be the value of y given that
![]()
(b) Solve the following simultaneous equation by matrix method
2x + y = 7
4x+3y = 17
(c) Find the image of (3, 5) after rotation of 270o about the origin in anticlockwise direction.
14. (a) If f(x) is the function such that
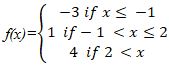
- Sketch the graph of f(x)
- State the domain and range of f(x)
(b) A transport company is hired to transport 420 people it has two types, P and Q of vehicle to be used. Type P carries 35 passengers and type Q carries 14 passengers. There are at least 10 vehicles of type Q and not more than 9 vehicles of type P. Write down inequalities to represent this information.
FORM FOUR MATHEMATICS EXAM SERIES 71
FORM FOUR MATHEMATICS EXAM SERIES 71
THE UNITED REPUBLIC OF TANZANIA, PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
MTWARA REGION
FORM FOUR TERMINAL EXAMINATION
041 BASIC MATHEMATICS
Time: 3 Hours MAY, 2021
INSTRUCTIONS
1. This paper consist of 14 compasaryquestions in section A and B
2. Answer all questions.
3. Necta mathematical table only, graph paper and geometric instruction may be used when necesary
4. Write your examination number at the top of a right corner of every page.
5. Use R = 6400Km and π = 3.14
| FOR EXAMINER’S USE ONLY | ||
| QUESTION | SCORE | INITIALS OF EXAMINER |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| TOTAL | ||
1. (a) Round off
(i) 9.67 to ones
(ii) 0.205 to 1 decimal place
(iii) 0.0197 to 1 significant figure.
(b) Express 0.83? in form of a/b where “a” and “b” are integers.
2. (a) Find the value of X in (1)3x−1 = 1 3
(b) Find the value of y from 2 loga y = 4 loga 5 − 2 loga 5
3. (a) Given that U = {Red, Green, White, Black, Yellow } and
A = {Black, White, Red };
Find the value of n(A)′
(b) Find the probability that a number will be selected at random from numbers −3, −2, 0, 3, 4 and 6 will be a solution of an equation x2 − x − 6 = 0
4. (a) Given vectors a −3i + 2j, b = 8i − 3j and c = 2i + 4j, find the vector d = 3a − b + ![]() c
c
(b) The point A(5, −7) is the vertex of the right angle of right angled triangle whose hypotenuse lies along the line 6x − 13y = 39. A second vertex of a triangle is B(0, −3). Find the remaining vertex C(x, y)
5. (a) In a triangle ABC, find its area if AB = 8cm, BC = 11.3cm and AB?C = 30
(b) If a polygons x and y are similar and their area are 16cm2 and 49cm2 respectively, what is the length of a side of polygon y if the corresponding side of polygon x is 28cm?
6. (a) If 10 people can cultivate a farm for 2 days in 3 hours, How many peolpe will cultivate the same farm for 1 day and 2 hours?
(b) Mr. Mtengula from Japan visited Mtwara. He had 5,000 Japanese Yen and wanted to change his money into US dollars. If 1 US dollar was equivalent to 20Tshs. How much US dollars did he get?
7. (a) An article sold at a loss of 40%. Calculate the selling price, if the loss made is 2,560/=
(b) Study the given trial balance and answer the questions that follow
| S/N | Details | Amounts (Tshs) | Amounts (Tshs) |
| Cash | 185,000 | | |
| Capital | | 200,000 | |
| Purchases | 110,000 | | |
| Sales | | 104,000 | |
| Water bills | 3000 | | |
| Advertising | 2000 | | |
| Telephone | 1000 | | |
| salaries | 3000 | | |
| 304,000 | 304,000 |
Prepare the following for the year ending 31st Dec 2010
(i) Trading and profit and loss account (ii) Balance sheet.
8. (a) The fifth term of an arthmetic progression (A.P) is zero and the tenth term is 10. Find the first term and the common difference.
(b) The sum of three consecutive terms of G.P is 19. If their product is 216, find those terms.
9. (a) (i) If θ = ![]() , find the value of
, find the value of
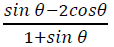
(ii) Without using mathematical table, evaluate Sin150
(b) A ladder reaches the top of a wall 18m high, when the other end on the ground is 8m from the wall. Find the length of that ladder.
10. (a) Solve for x from
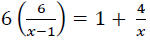
(b) Solve the following pair of simultaneous equations by elimination method.
2x + 3y = 12
3x = 7 + y
SECTION B (40 Marks)
11. Marks of 30 Students in mathematics were recorded as follow;
76, 44, 56, 36, 73, 20, 38, 27, 42, 61, 43, 52, 63, 72, 43, 46, 30, 77, 48, 41, 37, 53, 38, 55, 60, 51, 47, 33, 47, 58
(a) Construct the frequency distribution table with the class mark of 24.5, 34.5, 44.5 etc
(b) Calculate;
(i) Mean
(ii) Mode
(iii)Median
12. (a) Dodoma and Mtwara are located at (200S, 280E) and (200S, 580E) respectively. Find the distance between Dodoma and Mtwara in Nautical miles.
(b) A figure beolw shoes a right angled rectangular pyramid, find its total surface area.
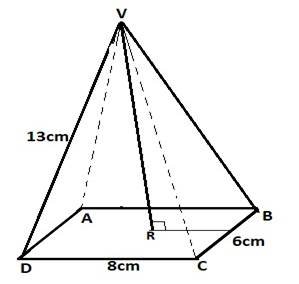
13. (a) Given that
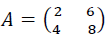
Find A−1
(b) Use the results obtained in part (a) to find the point of intersection the following system of simultaneous equations
2x + 6y = 22
4x + 8y = 32
(c)Find the image of the point obtained in paer (b) above under a rotation through 90° anticlockwise.
14. (a) A function fx is defined as
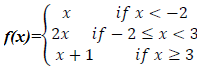
(i) Sketch the graph of f(x)
(ii) Find the domain and range of f(x)
(b) A farm is to be planted with sorghum and maize while observing the following constraints.
| Sorghum | maize | Max. total | |
| Days of labour per hectare | 4 | 2 | 20 |
| Labour cost per hectare | 1400 | 1200 | 8400 |
| Cost of fertilizer per hectare (shs) | 600 | 800 | 4800 |
If sorghum yields a profit of 800,000 shillings per hectare while maize yields 600,000 shillings per hectare. How many hectares should be planted with each crop for maximum profit?
FORM FOUR MATHEMATICS EXAM SERIES 48
FORM FOUR MATHEMATICS EXAM SERIES 48
THE PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
KILOSA DISTRICT COUNCIL
FORM FOUR PRE-MOCK JOINT EXAMINATION
041 BASIC MATHEMATICS
(For School Candidates Only)
TIME: 3:00 Hours March 15, 2021
Instructions
1. This paper consists of sections A and B with a total of fourteen (14) questions.
2. Answer all questions in section A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
3. All necessary working and answers for each question must be shown clearly.
4. NECTA mathematical tables and non-programmable calculators may be used.
5. Cellular phones, and any unauthorized materials are not allowed in the examination room.
6. Write your examination number on every page of your answer booklet(s)
SECTION A (60 Marks)
Answer all questions in this section.
 .
.
2. (a) Solve the value of x if
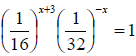
(b) If log 2 = 0.3010, without using mathematical tables, find the value of log 5
3. (a) A box contains 4 white balls and 5 black balls. Two balls are selected at random without replacement. Find the probability that
(i) Both are white balls
(ii) The first is black and the second is the white ball
(b) In a class of 15 students who take either Mathematics or Biology, 12 students take Mathematics, 8 students take Biology. If each student takes either subjects find by using formula the number of students who take Biology but not Mathematics.
4. (a) The gradient of line L1is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
(b) The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
5. (a) The area of the triangle ABC is 140 cm2, AB = 20, AC = 14cm, find the angle BAC
(b) Triangle XYZ is similar to triangle ABC and XY = 8 cm. If the area of the triangle XYZ is 24 cm2 and the area of the triangle ABC is 96 cm2. Calculate the length of AB.
6. (a) How many grams are there in 0.00912 tones
(b) The compression I of spring is directly proportional to the thrust, T exerted on it. If the thrust of 4N produces a compression of 0.8 cm, find:
(i) The compression when the thrust is 5 N
(ii) The thrust when the compression is 0.5 cm
7. (a) Maulid has to share eighty books with his young sisters Arafa and Jamila. He decided that for every two books Jamila gets, Arafa gets three books and he gets five![]() books. Find the number of books each gets
books. Find the number of books each gets
(b) Kijembe started the business on 16th March, 2020 with capital in cash 2,066,000/= March 17 bought goods for cash for 1,000,000/=
- 19 bought Shelves for cash 110,000/=
- 20 sold goods for cash 900,000/=
- 21 purchases goods for cash 800,000/=
- 22 sold goods for cash 1, 400,000/=
- 26 paid rent 300,000/=
Record the above transactions in Cash account ledger and extract a Trial balance.
8. (a). The product of a three terms of a geometric progression (GP) is 8000. If the first term is 4. Find the second term and third term
(b). Mahona invested a certain amount of money in a Savings Bank whose interest rate was 10% compounded annually. After two years he got 5000 shillings.
i. How much did he invest at the start? ii. How much did he receives as Interest at the end of two years.
9. (a) Find the value of
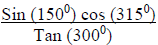
Without using mathematical tables.
(b) Calculate the angles of a triangle which has sides of lengths 4m, 5m and 7m
10. (a). Given that x2 –y2 = 27 and x + y = 9 find the value of xy
(b). Solve the equation 2x2 – 3x – 5 = 0 by completing the square.
SECTION B (40 Marks)
Answer all questions
11. (a) The number of workers absent in 52 working days is given in a cumulative frequency table below
| No.of absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 - 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find
- Percentage of workers who are absent at least for 20 days
- Median
(b) Find the angle x in the figure below
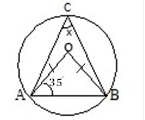
12. (a) A ship sails from point A (400S, 300W) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and π = 3.14(give your answer in nearest degree)
(b) VABCD is a pyramid with VA=VB=VC=VD=5cm and ABCD is a square base of sides 4cm each. Assume that the Centre of the base is at point N. Find
(i) The angle between VA and the base ABCD
(ii) The volume of the pyramid
13. (a)Find the value of t given that;
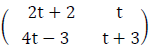
is a singular matrix
(b)Find the image of a line x − 10y = 7, when undergoes reflection at the line x = y then translated at a factor T = (−2, 2)
14. (a). A function F is defined by the formula f(x) = ![]() where x is a whole number i. If f(x) = 25 find the value of x
where x is a whole number i. If f(x) = 25 find the value of x
ii. Find the value of ![]()
(b). A craftsman wishes to decide how many of each type A and B charcoal stove he has to fabricate in order to maximize profit for this month. Unit profit for type A stove is shs. 1000 and Unit profit for type B is shs. 1500. Type A stove requires 1m2 of mild steel sheet per unit and type B requires 2m2. He has only 12 m2 of mild steel available. He can fabricate a total of 8 stoves of either type per month. How many of each type should he fabricate?
FORM FOUR MATHEMATICS EXAM SERIES 46
FORM FOUR MATHEMATICS EXAM SERIES 46
PRESIDENT’S OFFICE REGIONAL ADMINISTRATION AND LOCAL GOVERNMENT
FORM IV MOCK EXAMINATION 2020 DODOMA REGION
041BASIC MATHEMATICS
(For Both School and Private Candidates)
Time:3 HoursWednesday, 5th August 2020 a.m.
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions in section A and B. Each question in section A carries six (6) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables may be used.
- Cellular phones, calculators and any unauthorised materials are not allowed in the examination room.
- Write your examination number on every page of your answer booklet(s)
SECTION A (60 Marks)
Answer all questions in this section.
1. ![]()
![]()
![]()
![]()
![]()
2. ![]()
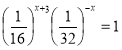
![]()
3. (a) A box contains 4 white balls and 5 black balls. Two balls are selected at random without replacement. Find the probability that
(i) Both are white balls
(ii) The first is black and the second is the white ball
(b) In a class of 15 students who take either Mathematics or Biology, 12 students take Mathematics, 8 students take Biology. If each student takes either subjects find by using formula the number of students who take Biology but not Mathematics.
4. (a) The gradient of line ![]() is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
is -2. Another line L2 is perpendicular to L1 and passes through point (-3, -2). What is the equation of L2?
(b) The distance between (1,5) and (k+5, k+1) is 8. Find K, given that it is positive
5.(a) The area of the triangle ABC is 140 cm2, AB = 20, AC = 14cm, find the angle BAC
(b) Triangle XYZ is similar to triangle ABC and XY = 8 cm. If the area of the triangle XYZ is 24 cm2 and the area of the triangle ABC is 96 cm2. Calculate the length of AB.
6.![]()
![]()
![]()
![]()
![]()
7. ![]()
![]()
![]()
![]() =
=
![]() /=
/=
19 bought Shelves for cash 110,000/=
20 sold goods for cash 900,000/=
21 purchases goods for cash 800,000/=
22 sold goods for cash 1, 400,000/=
26 paid rent 300,000/=
Record the above transactions in Cash account ledger and extract a Trial balance.
8. (a). The product of a three terms of a geometric progression (GP) is 8000. If the first term is 4. Find the second term and third term
(b). Mahona invested a certain amount of money in a Savings Bank whose interest rate was 10% compounded annually. After two years he got 5000 shillings.
- How much did he invest at the start?
- How much did he receives as Interest at the end of two years.
9. (a) Find the value of
Sin (1500) cos (3150) Without using mathematical tables
Tan (3000)
(b) Calculate the angles of a triangle which has sides of lengths 4m, 5m and 7m
10.(a). Given that x2 –y2 = 27 and x + y = 9 find the value of xy
(b). Solve the equation 2x2 – 3x – 5 = 0 by completing the square.
SECTION B (40 Marks)
Answer all questions
11. (a) The number of workers absent in 52 working days is given in a cumulative frequency table below
| No.of absent | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 | 25 - 29 |
| Cumulative frequency | 5 | 13 | 30 | 45 | 48 | 52 |
Find (i) Percentage of workers who are absent at least for 20 days
(ii) Median
(b) Find the angle x in the figure below
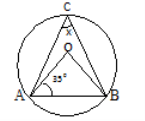
12. (a) A ship sails from point A (40![]() ) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and
) due west along the same latitude to point B for 1000km. Find the latitude and longitude of point B. Use R=6370km and ![]() (give your answer in nearest degree)
(give your answer in nearest degree)
(b) VABCD is a pyramid with VA=VB=VC=VD=5cm and ABCD is a square base of sides 4cm each. Assume that the centre of the base is at point N. Find
(i) The angle between VA and the base ABCD
(ii) The volume of the pyramid
13. ![]()
![]()
![]()
![]()
![]()
14. (a). A function F is defined by the formula f(x) = ![]() where x is a whole number
where x is a whole number
- If f(x) = 25 find the value of x
- Find the value of
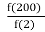
(b). A craftsman wishes to decide how many of each type A and B charcoal stove he has to fabricate in order to maximize profit for this month. Unit profit for type A stove is shs. 1000 and Unit profit for type B is shs. 1500. Type A stove requires 1m2 of mild steel sheet per unit and type B requires 2m2. He has only 12 m2 of mild steel available. He can fabricate a total of 8 stoves of either type per month. How many of each type should he fabricate?
FORM FOUR MATHEMATICS EXAM SERIES 9
FORM FOUR MATHEMATICS EXAM SERIES 9
Hub App
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256